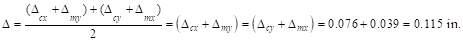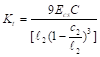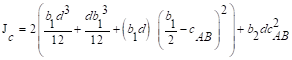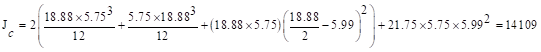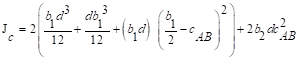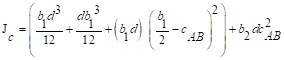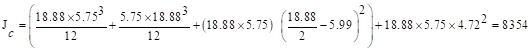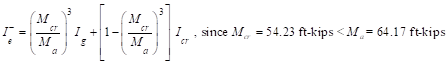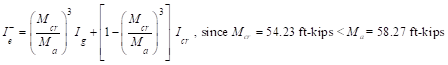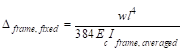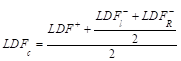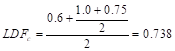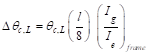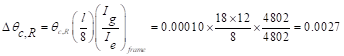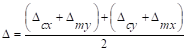Code
Building Code Requirements
for Structural Concrete (ACI 318-14) and Commentary (ACI 318R-14)
Minimum Design Loads for
Buildings and Other Structures (ASCE/SEI 7-10)
International Code Council,
2012 International Building Code, Washington, D.C., 2012
Reference
Notes on ACI 318-11 Building
Code Requirements for Structural Concrete, Twelfth Edition, 2013 Portland Cement
Association, Example 20.1
Concrete Floor Systems
(Guide to Estimating and Economizing), Second Edition, 2002 David A. Fanella
Simplified Design of Reinforced
Concrete Buildings, Fourth Edition, 2011 Mahmoud E. Kamara and Lawrence C.
Novak
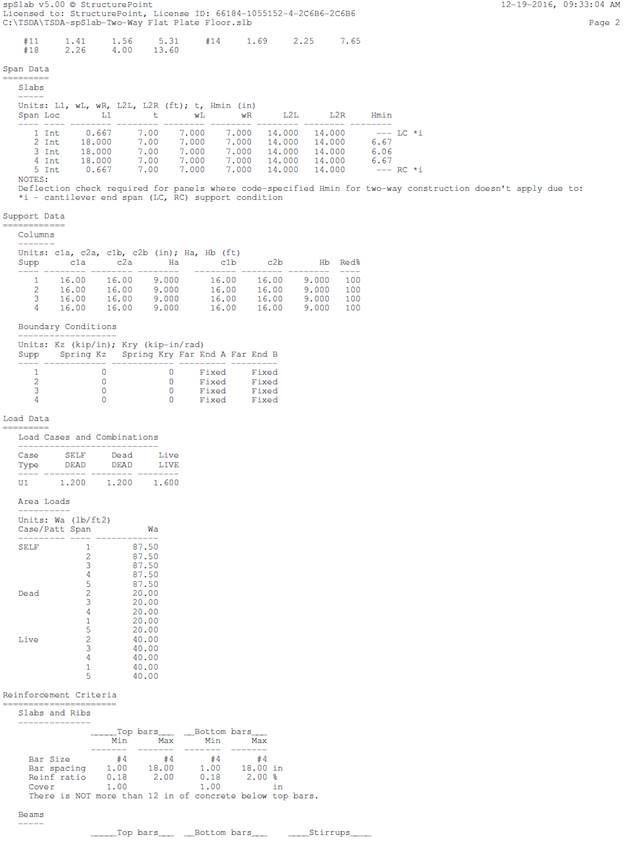
Design Data
Floor-to-Floor Height = 9 ft
(provided by architectural drawings)
Superimposed Dead Load, SDL =20 psf for framed
partitions, wood studs plaster 2 sides
ASCE/SEI 7-10 (Table C3-1)
Live Load, LL = 40 psf for
Residential floors ASCE/SEI
7-10 (Table 4-1)
fc’ = 4000 psi (for slabs)
fc’ = 6000 psi (for columns)
fy = 60,000 psi
Required fire resistance
rating = 2 hours
Solution
a.
Slab minimum
thickness - Deflection
ACI 318-14 (8.3.1.1)
In
this example deflection will be calculated and checked to satisfy project
deflection limits. Minimum member thickness and depths from ACI 318-14 will be
used for preliminary sizing.
Using
ACI 318-14 minimum slab thickness for two-way construction without interior
beams in Table 8.3.1.1.
Exterior Panels: 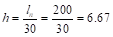 in. ACI
318-14 (Table 8.3.1.1)
in. ACI
318-14 (Table 8.3.1.1)
But not less than 5 in.
ACI 318-14 (8.3.1.1(a))
Interior Panels: 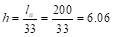 in. ACI
318-14 (Table 8.3.1.1)
in. ACI
318-14 (Table 8.3.1.1)
But not less
than 5 in. ACI
318-14 (8.3.1.1(a))
Where ln
= length of clear span in the long direction = 216 – 16 = 200 in.
Try 7 in. slab for all panels
(self-weight = 87.5 psf)
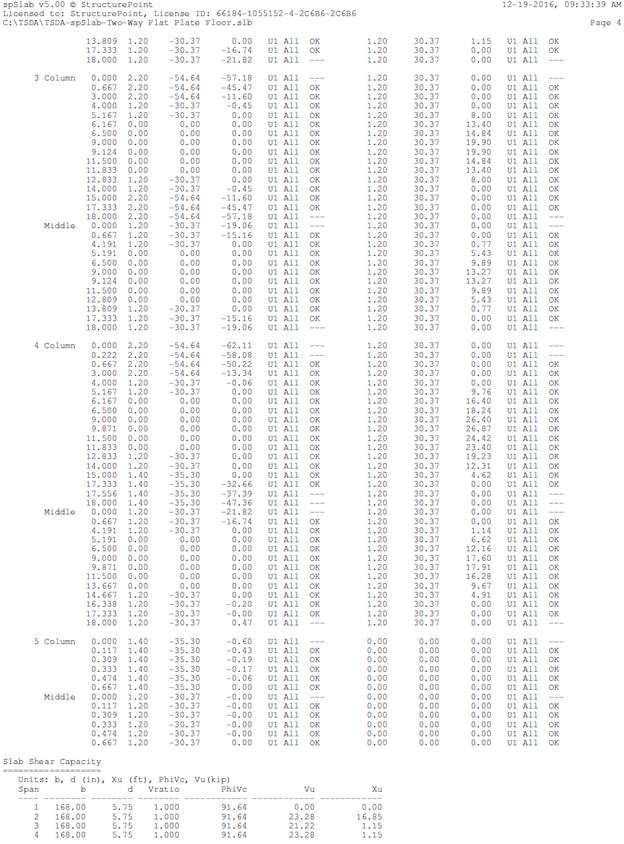
b. Slab shear strength – one way shear
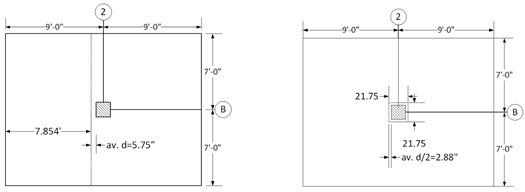
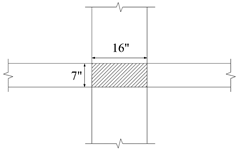
Evaluate the average
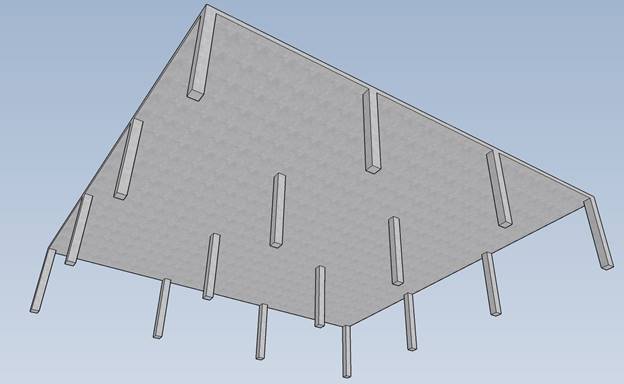
effective depth (Figure 2):
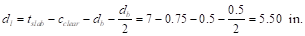
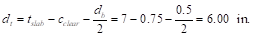
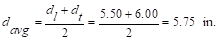
Where:
cclear = 3/4 in. for # 4 steel bar ACI
318-14 (Table 20.6.1.3.1)
db = 0.5 in. for # 4 steel bar
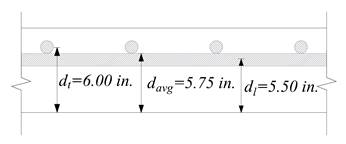
Figure 2 -
Two-Way Flat Concrete Floor System
Factored dead load, 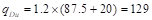 psf
psf
Factored live load, 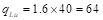 psf
ACI 318-14 (5.3.1)
psf
ACI 318-14 (5.3.1)
Total factored load 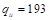 psf
psf
Check the adequacy of slab thickness for beam action (one-way shear) ACI
318-14 (22.5)
at an interior column:
Consider a 12-in. wide
strip. The critical section for one-way shear is located at a distance d,
from the face of support (see Figure 3)
Tributary area for one-way
shear is 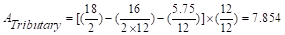 ft2
ft2
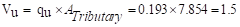 kips
kips
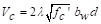 ACI 318-14 (Eq. 22.5.5.1)
ACI 318-14 (Eq. 22.5.5.1)
where 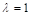 for normal weight concrete
for normal weight concrete
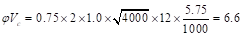 kips
kips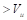
Slab thickness of 7 in.
is adequate for one-way shear.
c.
Slab shear
strength – two-way shear
Check the adequacy of
slab thickness for punching shear (two-way shear) at an interior column (Figure
4):
Tributary area for two-way
shear is 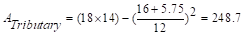 ft2
ft2
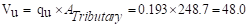 kips
kips
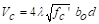 (For square interior column) ACI
318-14 (Table 22.6.5.2(a))
(For square interior column) ACI
318-14 (Table 22.6.5.2(a))
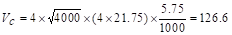 kips
kips
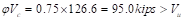
Slab thickness of 7 in.
is adequate for two-way shear.
d. Column dimensions - axial load
Check the adequacy of
column dimensions for axial load:
Tributary area for
interior column is 
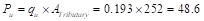 kips
kips
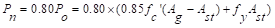 (For square interior column) ACI
318-14 (22.4.2)
(For square interior column) ACI
318-14 (22.4.2)
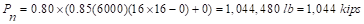
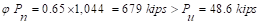
Column dimensions of 16 in. x 16 in.
are adequate for axial load.
ACI 318 states that a slab system
shall be designed by any procedure satisfying equilibrium and geometric
compatibility, provided that strength and serviceability criteria are
satisfied. Distinction of two-systems from one-way systems is given by ACI
318-14 (R8.10.2.3 & R8.3.1.2).
ACI 318 permits the use of Direct
Design Method (DDM) and Equivalent Frame Method (EFM) for the gravity load
analysis of orthogonal frames and is applicable to flat plates, flat slabs, and
slabs with beams. The following sections outline the solution per DDM, EFM, and
spSlab software respectively.
Two-way slabs satisfying the
limits in ACI 318-14 (8.10.2) are permitted to be designed
in accordance with the DDM.
There
is a minimum of three continuous spans in each direction ACI 318-14 (8.10.2.1)
Successive
span lengths are equal
ACI 318-14 (8.10.2.2)
Long-to-short
span ratio is 1.29 < 2
ACI 318-14 (8.10.2.3)
Columns
are not offset
ACI 318-14 (8.10.2.4)
Loads
are uniformly distributed over the entire panel ACI
318-14 (8.10.2.5)
Service
live-to-dead load ratio of 0.37 <
2.0 ACI 318-14 (8.10.2.6)
Slab
system is without beams and this requirement is not applicable ACI 318-14 (8.10.2.7)
Since
all the criteria are met, Direct Design Method can be utilized.
a.
Calculate the
total factored static moment:
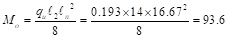 ft-kips
ACI 318-14 (8.10.3.2)
ft-kips
ACI 318-14 (8.10.3.2)
b.
Distribute the
total factored moment, 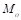 , in an interior and end span:
ACI 318-14
(8.10.4)
, in an interior and end span:
ACI 318-14
(8.10.4)
|
Table 1 - Distribution of Mo
along the span
|
|
Location
|
Total Design Strip Moment,
MDS (ft-kips)
|
|
Exterior Span
|
Exterior Negative
|
0.26 x Mo = 24.3
|
|
Positive
|
0.52 x Mo = 48.7
|
|
Interior Negative
|
0.70 x Mo = 65.5
|
|
Interior Span
|
Positive
|
0.35 x Mo = 32.8
|
c.
Calculate the
column strip moments.
ACI 318-14
(8.10.5)
That
portion of negative and positive total design strip moments not resisted by
column strips shall be proportionally assigned to corresponding two half-middle
strips.
ACI 318-14 (8.10.6.1)
|
Table 2 - Lateral
Distribution of the Total Design Strip Moment, MDS
|
|
Location
|
Total Design Strip
Moment, MDS
(ft-kips)
|
Column Strip
Moment, (ft-kips)
|
Moment in Two
Half Middle Strips,
(ft-kips)
|
|
Exterior Span
|
Exterior
Negative*
|
24.3
|
1.00 x MDS = 24.3
|
0.00 x MDS = 0.0
|
|
Positive
|
48.7
|
0.60 x MDS = 29.2
|
0.40 x MDS = 19.5
|
|
Interior
Negative*
|
65.5
|
0.75 x MDS = 49.1
|
0.25 x MDS = 16.4
|
|
Interior Span
|
Positive
|
32.8
|
0.60 x MDS = 19.7
|
0.40 x MDS = 13.1
|
|
* All negative
moments are at face of support.
|
a.
Determine
flexural reinforcement required for column and middle strips at all critical
sections
The following calculation is
for the exterior span exterior negative location of the column strip.
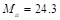 ft-kips
ft-kips
Use average davg = 5.75 in.
To
determine the area of steel, assumptions have to be made whether the section is
tension or compression controlled, and regarding the distance between the
resultant compression and tension forces along the slab section (jd). In
this example, tension-controlled section will be assumed so the reduction factor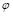 is equal to 0.9, and jd will be taken equal to 0.95d.
The assumptions will be verified once the area of steel in finalized.
is equal to 0.9, and jd will be taken equal to 0.95d.
The assumptions will be verified once the area of steel in finalized.
Assume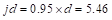 in.
in.
Column
strip width, 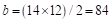 in.
in.
Middle
strip width, 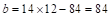 in.
in.
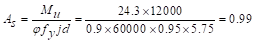 in2
in2
Recalculate ‘a’ for the
actual As = 0.99 in.2:
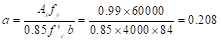 in
in
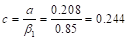 in
in
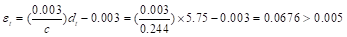
Therefore, the assumption that section is tension-controlled
is valid.
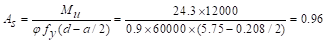 in2
in2
Min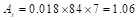 in2
in2 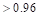 in2
ACI 318-14 (24.4.3.2)
in2
ACI 318-14 (24.4.3.2)
Maximum spacing 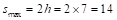 in
in 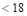 in ACI
318-14 (8.7.2.2)
in ACI
318-14 (8.7.2.2)
Provide 6 - #4 bars with 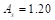 in2 and
in2 and 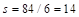 in
in 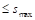
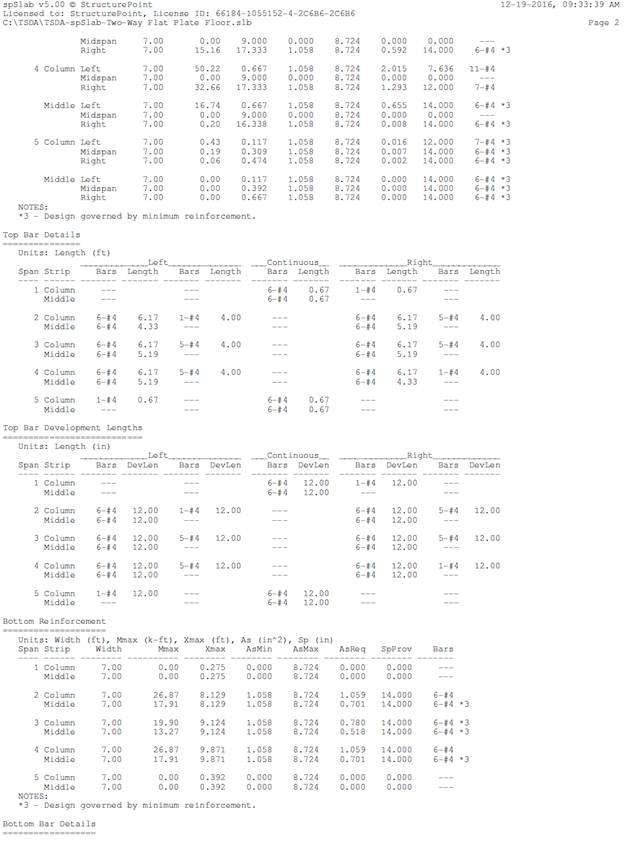
Based on the procedure outlined above, values for all
span locations are given in Table 3.
|
Table 3 -
Required Slab Reinforcement for Flexure (DDM)
|
|
Span
Location
|
Mu
(ft-kips)
|
b
(in.)
|
d
(in.)
|
As Req’d
for
flexure (in2)
|
Min As
(in2)
|
Reinforcement
Provided
|
As Prov.
for
flexure (in2)
|
|
End Span
|
|
Column
Strip
|
Exterior Negative
|
24.3
|
84
|
5.75
|
0.96
|
1.06
|
6-#4
|
1.2
|
|
Positive
|
29
|
84
|
5.75
|
1.15
|
1.06
|
6-#4
|
1.2
|
|
Interior Negative
|
49.6
|
84
|
5.75
|
1.99
|
1.06
|
10-#4
|
2
|
|
Middle
Strip
|
Exterior Negative
|
0
|
84
|
5.75
|
0
|
1.06
|
6-#4
|
1.2
|
|
Positive
|
19.7
|
84
|
5.75
|
0.77
|
1.06
|
6-#4
|
1.2
|
|
Interior Negative
|
15.9
|
84
|
5.75
|
0.62
|
1.06
|
6-#4
|
1.2
|
|
Interior
Span
|
|
Column
Strip
|
Positive
|
19.7
|
84
|
5.75
|
0.77
|
1.06
|
6-#4
|
1.2
|
|
Middle
Strip
|
Positive
|
13.1
|
84
|
5.75
|
0.51
|
1.06
|
6-#4
|
1.2
|
b.
Calculate
additional slab reinforcement at columns for moment transfer between slab and
column
The factored slab moment
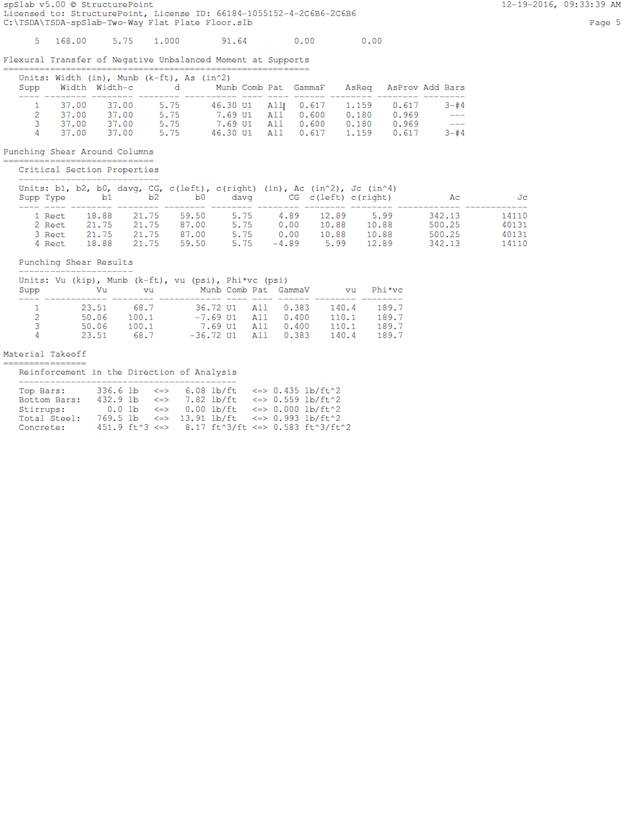
resisted by the column (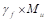 ) shall be assumed to be transferred by flexure.
Concentration of reinforcement over the column by closer spacing or additional
reinforcement shall be used to resist this moment. The fraction of slab moment
not calculated to be resisted by flexure shall be assumed to be resisted by
eccentricity of shear. ACI
318-14 (8.4.2.3)
) shall be assumed to be transferred by flexure.
Concentration of reinforcement over the column by closer spacing or additional
reinforcement shall be used to resist this moment. The fraction of slab moment
not calculated to be resisted by flexure shall be assumed to be resisted by
eccentricity of shear. ACI
318-14 (8.4.2.3)
Portion of the unbalanced
moment transferred by flexure is 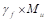 ACI 318-14 (8.4.2.3.1)
ACI 318-14 (8.4.2.3.1)
Where
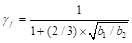 ACI 318-14 (8.4.2.3.2)
ACI 318-14 (8.4.2.3.2)
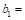 Dimension of the critical section
Dimension of the critical section 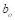 measured in the direction of the span for which
moments are determined in ACI 318, Chapter 8 (see Figure 5).
measured in the direction of the span for which
moments are determined in ACI 318, Chapter 8 (see Figure 5).
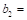 Dimension of the critical section
Dimension of the critical section 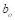 measured in the direction perpendicular to
measured in the direction perpendicular to 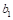 in ACI 318, Chapter 8 (see Figure 5).
in ACI 318, Chapter 8 (see Figure 5).
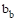 = Effective slab width =
= Effective slab width =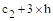 ACI 318-14 (8.4.2.3.3)
ACI 318-14 (8.4.2.3.3)
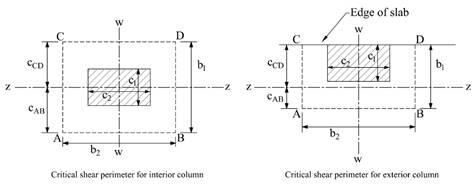
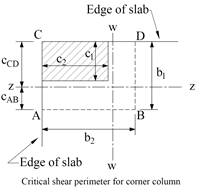
Figure 5 – Critical Shear Perimeters for Columns
|
Table 4 -
Additional Slab Reinforcement required for moment transfer between slab and
column (DDM)
|
|
Span
Location
|
Mu*
(ft-kips)
|
γf
|
γf
Mu
(ft-kips)
|
Effective
slab
width, bb
(in.)
|
d
(in.)
|
As
req’d
within bb
(in2)
|
As
prov. For
flexure
within bb
(in2)
|
Add’l
Reinf.
|
|
End Span
|
|
Column Strip
|
Exterior
Negative
|
24.3
|
0.62
|
15.1
|
37
|
5.75
|
0.6
|
0.53
|
1-#4
|
|
Interior
Negative
|
0.0
|
0.60
|
0.0
|
37
|
5.75
|
0.0
|
0.97
|
-
|
|
*Mu is taken at the centerline
of the support in Equivalent Frame Method solution.
|
a.
Interior columns:
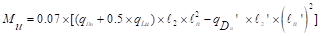 ACI 318-14 (8.10.7.2)
ACI 318-14 (8.10.7.2)
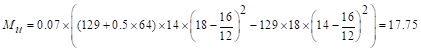 ft-kips
ft-kips
With the same column size and length above and below
the slab,
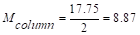 ft-kips
ft-kips
b. Exterior Columns:
Total exterior negative
moment from slab must be transferred directly to the column: 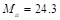 ft-kips. With the same column size and length above
and below the slab,
ft-kips. With the same column size and length above
and below the slab,
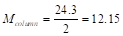 ft-kips
ft-kips
The
moments determined above are combined with the factored axial loads (for each
story) for design of column sections as shown later in this example.
EFM is the
most comprehensive and detailed procedure provided by the ACI 318 for the analysis
and design of two-way slab systems where the structure is modeled by a series
of equivalent frames (interior and exterior) on column lines taken
longitudinally and transversely through the building.
The equivalent frame consists of three
parts:
1) Horizontal slab-beam strip, including
any beams spanning in the direction of the frame. Different values of moment of
inertia along the axis of slab-beams should be taken into account where the
gross moment of inertia at any cross section outside of joints or column
capitals shall be taken, and the moment of inertia of the slab-beam at the
face of the column, bracket or capital divide by the quantity (1-c2/l2)2
shall be assumed for the calculation of the moment of inertia of slab-beams
from the center of the column to the face of the column, bracket or capital. ACI
318-14 (8.11.3)
2) Columns or other vertical supporting
members, extending above and below the slab. Different values of moment of
inertia along the axis of columns should be taken into account where the moment
of inertia of columns from top and bottom of the slab-beam at a joint shall be
assumed to be infinite, and the gross cross section of the concrete is
permitted to be used to determine the moment of inertia of columns at any cross
section outside of joints or column capitals. ACI
318-14 (8.11.4)
3) Elements of the structure (Torsional
members) that provide moment transfer between the horizontal and vertical
members. These elements shall be assumed to have a constant cross section
throughout their length consisting of the greatest of the following: (1)
portion of slab having a width equal to that of the column, bracket, or capital
in the direction of the span for which moments are being determined, (2)
portion of slab specified in (1) plus that part of the transverse beam above
and below the slab for monolithic or fully composite construction, (3) the
transverse beam includes that portion of slab on each side of the beam
extending a distance equal to the projection of the beam above or below the
slab, whichever is greater, but not greater than four times the slab
thickness. ACI 318-14 (8.11.5)
In
EFM, live load shall be arranged in accordance with 6.4.3 which requires slab
systems to be analyzed and designed for the most demanding set of forces
established by investigating the effects of live load placed in various
critical patterns. ACI 318-14 (8.11.1.2 & 6.4.3)
Complete
analysis must include representative interior and exterior equivalent frames in
both the longitudinal and transverse directions of the floor
ACI
318-14 (8.11.2.1)
Panels shall be rectangular, with
a ratio of longer to shorter panel dimensions, measured center-to-center of
supports, not to exceed 2. ACI 318-14 (8.10.2.3)
Determine moment distribution factors and fixed-end
moments for the equivalent frame members. The moment distribution procedure
will be used to analyze the equivalent frame. Stiffness factors 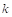 , carry over factors COF, and fixed-end moment factors
FEM for the slab-beams and column members are determined using the design aids tables
at Appendix 20A of PCA Notes on ACI 318-11. These
calculations are shown below.
, carry over factors COF, and fixed-end moment factors
FEM for the slab-beams and column members are determined using the design aids tables
at Appendix 20A of PCA Notes on ACI 318-11. These
calculations are shown below.
a.
Flexural
stiffness of slab-beams at both ends, 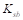 .
.
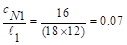 ,
, 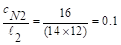
For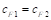 , stiffness factors,
, stiffness factors, 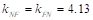 PCA Notes on
ACI 318-11 (Table A1)
PCA Notes on
ACI 318-11 (Table A1)
Thus,
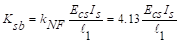 PCA
Notes on ACI 318-11 (Table A1)
PCA
Notes on ACI 318-11 (Table A1)
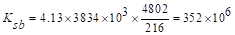 in.-lb
in.-lb
where,
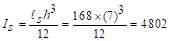 in4
in4
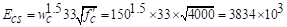 psi
ACI 318-14 (19.2.2.1.a)
psi
ACI 318-14 (19.2.2.1.a)
Carry-over factor COF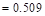 PCA Notes on ACI 318-11 (Table A1)
PCA Notes on ACI 318-11 (Table A1)
Fixed-end moment FEM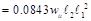 PCA
Notes on ACI 318-11 (Table A1)
PCA
Notes on ACI 318-11 (Table A1)
b.
Flexural
stiffness of column members at both ends, 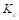 .
.
Referring
to Table A7, Appendix 20A, 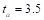 in.,
in.,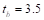 in.,
in.,
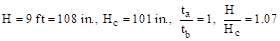
Thus,
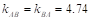 by interpolation.
by interpolation.
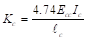 PCA Notes on ACI 318-11 (Table A7)
PCA Notes on ACI 318-11 (Table A7)
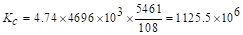 in.-lb
in.-lb
Where 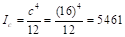 in.
in.
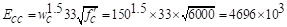 psi ACI
318-14 (19.2.2.1.a)
psi ACI
318-14 (19.2.2.1.a)
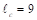 ft
ft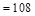 in.
in.
c.
Torsional
stiffness of torsional members,  .
.
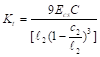 ACI 318-14 (R.8.11.5)
ACI 318-14 (R.8.11.5)
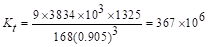 in.-lb
in.-lb
Where 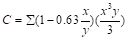 ACI 318-14 (Eq. 8.10.5.2b)
ACI 318-14 (Eq. 8.10.5.2b)
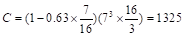 in4.
in4.
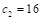 in., and
in., and 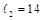 ft
ft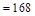 in.
in.
d.
Equivalent column
stiffness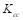 .
.
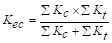
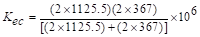

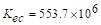
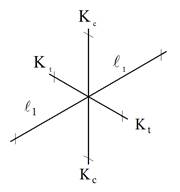 in.-lb
in.-lb
Where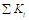 is for two torsional members one on each side of the
column, and
is for two torsional members one on each side of the
column, and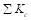 is for the upper and lower columns at the slab-beam
joint of an intermediate floor.
is for the upper and lower columns at the slab-beam
joint of an intermediate floor.
e.
Slab-beam joint
distribution factors, DF.
At
exterior joint,
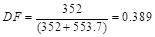
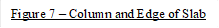
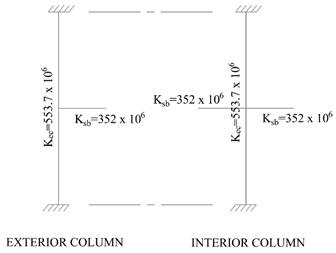
At
interior joint,
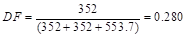
COF
for slab-beam 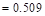
Determine negative and positive
moments for the slab-beams using the moment distribution method. Since the
unfactored live load does not exceed three-quarters of the unfactored dead
load, design moments are assumed to occur at all critical sections with full
factored live on all spans. ACI 318-14 (6.4.3.2)
a. Factored load and Fixed-End Moments
(FEM’s).
Factored
dead load 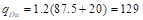 psf
psf
Factored
live load 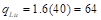 psf
psf
Factored load 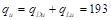 psf
psf
FEM’s for slab-beams 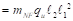 PCA Notes on ACI 318-11 (Table A1)
PCA Notes on ACI 318-11 (Table A1)
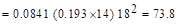 ft-kips
ft-kips
b. Moment distribution. Computations are
shown in Table 5. Counterclockwise rotational moments acting on the member ends
are taken as positive. Positive span moments are determined from the following
equation:
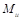 (midspan)
(midspan)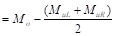
Where
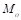 is the moment at the midspan for a simple beam.
is the moment at the midspan for a simple beam.
When
the end moments are not equal, the maximum moment in the span does not occur at
the midspan, but its value is close to that midspan for this example.
Positive
moment in span 1-2:
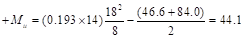 ft-kips
ft-kips
|
Positive moment span
2-3:
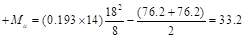 ft-kips ft-kips
|
|
Table 5 – Moment Distribution for Equivalent Frame
|
|

|
|
Joint
|
1
|
2
|
3
|
4
|
|
Member
|
1-2
|
2-1
|
2-3
|
3-2
|
3-4
|
4-3
|
|
DF
|
0.389
|
0.280
|
0.280
|
0.280
|
0.280
|
0.389
|
|
COF
|
0.509
|
0.509
|
0.509
|
0.509
|
0.509
|
0.509
|
|
FEM
|
+73.8
|
-73.8
|
+73.8
|
-73.8
|
+73.8
|
-73.8
|
|
Dist
CO
Dist
CO
Dist
CO
Dist
CO
Dist
|
-28.7
0.0
0.0
2.1
-0.8
0.3
-0.1
0.1
0.0
|
0.0
-14.6
4.1
0.0
0.6
-0.4
0.2
-0.1
0.0
|
0.0
0.0
4.1
-2.1
0.6
-0.3
0.2
-0.1
0.0
|
0.0
0.0
-4.1
2.1
-0.6
0.3
-0.2
0.1
0.0
|
0.0
14.6
-4.1
0.0
-0.6
0.4
-.02
0.1
0.0
|
28.7
0.0
0.0
-2.1
0.8
-0.3
0.1
-0.1
0.0
|
|
Neg. M
|
46.6
|
-84.0
|
76.2
|
-76.2
|
84.0
|
-46.6
|
|
M at midspan
|
44.1
|
33.2
|
44.1
|
Positive and negative factored
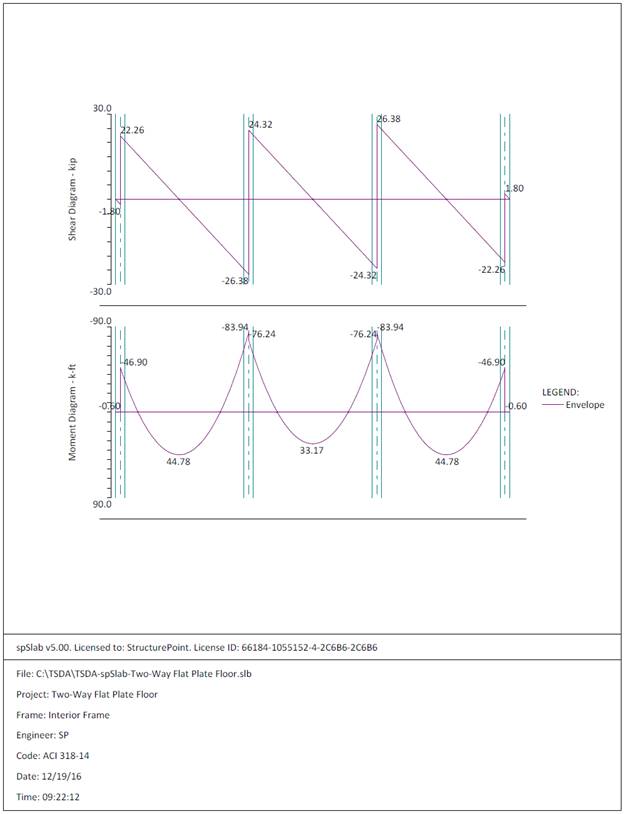
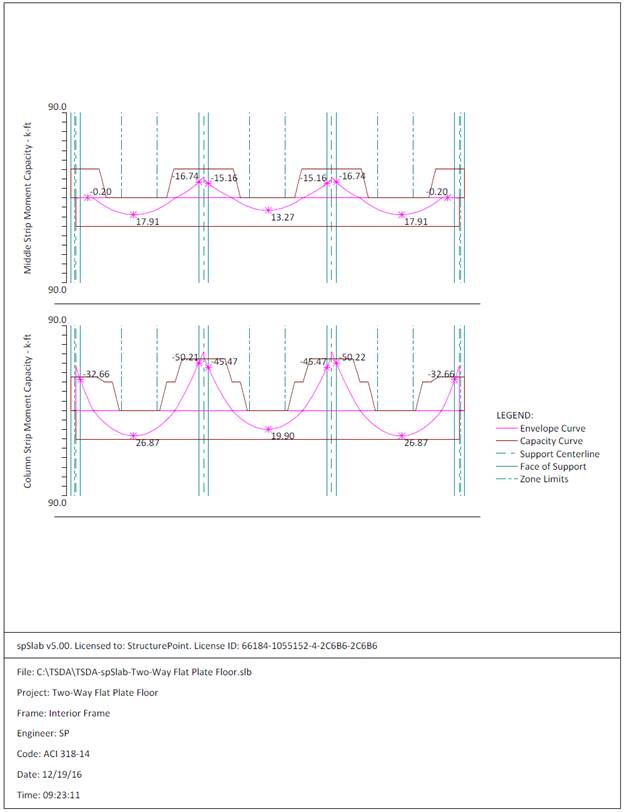
moments for the slab system in the direction of analysis are plotted in Figure 9.
The negative moments used for design are taken at the faces of supports
(rectangle section or equivalent rectangle for circular or polygon sections) but
not at distances greater than 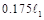 from the centers of supports.
ACI
318-14 (8.11.6.1)
from the centers of supports.
ACI
318-14 (8.11.6.1)
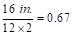 ft
ft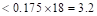 ft (use face of support location)
ft (use face of support location)
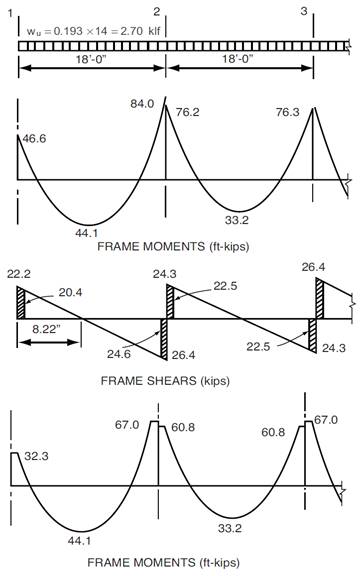
Figure 9 - Positive and
Negative Design Moments for Slab-Beam (All Spans Loaded with Full Factored Live
Load)
a. Check whether the moments calculated above can take
advantage of the reduction permitted by ACI 318-14 (8.11.6.5):
If the slab system analyzed using EFM within the
limitations of ACI 318-14 (8.10.2), it is permitted by the
ACI code to reduce the calculated moments obtained from EFM in such proportion
that the absolute sum of the positive and average negative design moments need
not exceed the value obtained from the following equation:
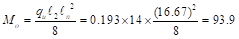 ft-kips ACI
318-14 (Eq. 8.10.3.2)
ft-kips ACI
318-14 (Eq. 8.10.3.2)
End
spans: 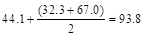 ft-kips
ft-kips
Interior
span: 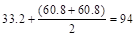 ft-kips
ft-kips
The
total design moments from the Equivalent Frame Method yield a static moment
equal to that given by the Direct Design Method and no appreciable reduction
can be realized.
b.
Distribute factored moments to column and middle strips:
After the negative and positive moments have been
determined for the slab-beam strip, the ACI code permits the distribution of
the moments at critical sections to the column strips, beams (if any), and
middle strips in accordance with the DDM.
ACI 318-14 (8.11.6.6)
Distribution
of factored moments at critical sections is summarized in Table 6.
|
Table 6 - Distribution of
factored moments
|
|
|
Slab-beam Strip
|
Column Strip
|
Middle Strip
|
|
Moment
(ft-kips)
|
Percent
|
Moment
(ft-kips)
|
Percent
|
Moment
(ft-kips)
|
|
End Span
|
Exterior Negative
|
32.3
|
100
|
32.3
|
0
|
0
|
|
Positive
|
44.1
|
60
|
26.5
|
40
|
17.7
|
|
Interior Negative
|
67
|
75
|
50.3
|
25
|
16.7
|
|
Interior Span
|
Negative
|
60.8
|
75
|
45.6
|
25
|
15.2
|
|
Positive
|
33.2
|
60
|
19.9
|
40
|
13.2
|
a. Determine flexural reinforcement required for strip
moments
The
flexural reinforcement calculation for the column strip of end span – exterior
negative location is provided below.
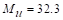 ft-kips
ft-kips
Use
average davg = 5.75 in.
To determine the area of steel, assumptions have to be
made whether the section is tension or compression controlled, and regarding
the distance between the resultant compression and tension forces along the
slab section (jd). In this example, tension-controlled section will be
assumed so the reduction factor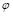 is equal to 0.9, and jd will be taken equal to 0.95d.
The assumptions will be verified once the area of steel in finalized.
is equal to 0.9, and jd will be taken equal to 0.95d.
The assumptions will be verified once the area of steel in finalized.
Assume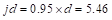 in.
in.
Column
strip width, 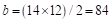 in.
in.
Middle
strip width, 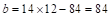 in.
in.
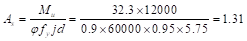 in.2
in.2
Recalculate
‘a’ for the actual As = 1.31 in.2: 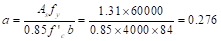 in.
in.
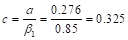 in.
in.
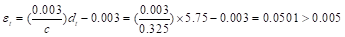
Therefore,
the assumption that section is tension-controlled is valid.
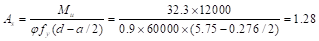 in.2
in.2
Min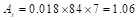 in2
in2 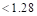 in.2 ACI
318-14 (24.4.3.2)
in.2 ACI
318-14 (24.4.3.2)
Maximum spacing 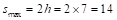 in.
in. 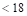 in. ACI
318-14 (8.7.2.2)
in. ACI
318-14 (8.7.2.2)
Provide
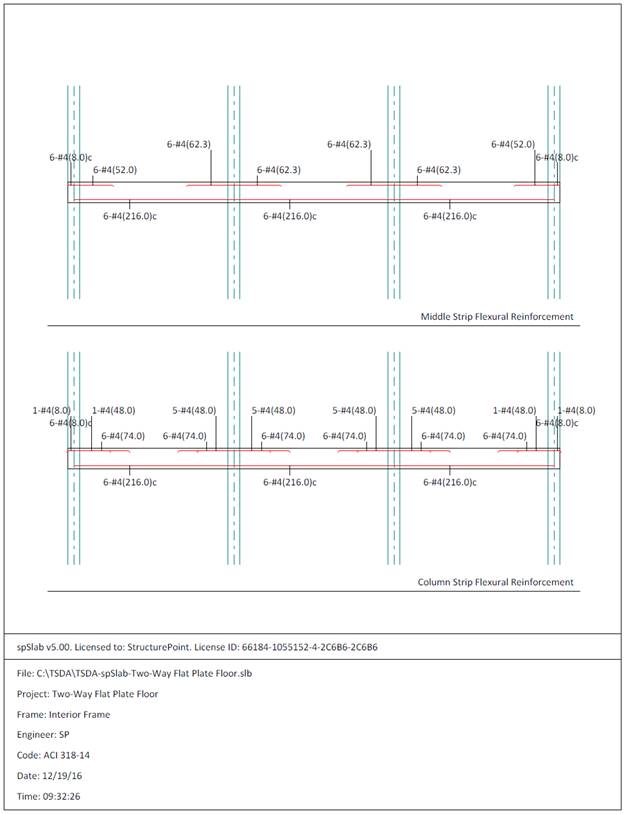
7 - #4 bars with As = 1.40 in.2 and s = 84/7 = 12 in. 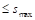
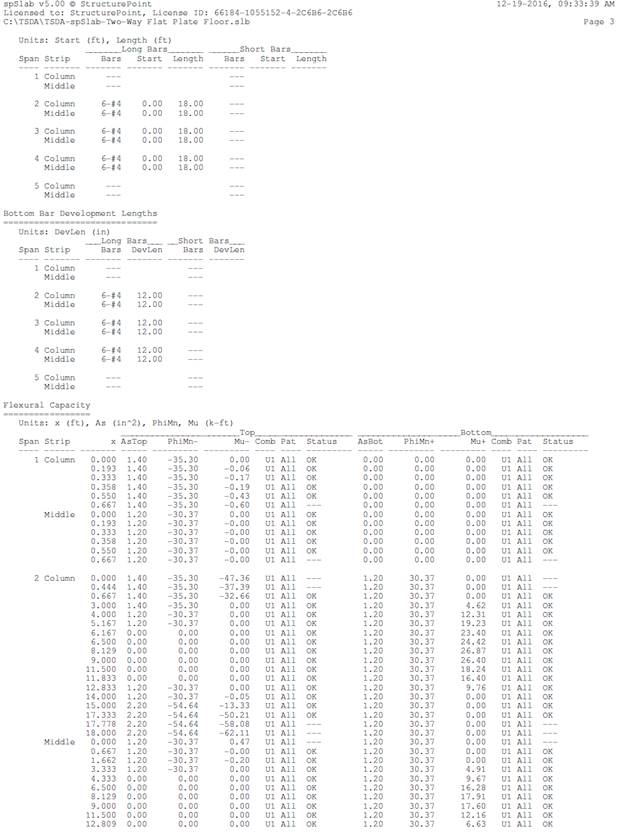
Based
on the procedure outlined above, values for all span locations are given in
Table 7.
|
Table 7 -
Required Slab Reinforcement for Flexure [Equivalent Frame Method (EFM)]
|
|
Span
Location
|
Mu
(ft-kips)
|
b *
(in.)
|
d **
(in.)
|
As Req’d
for flexure (in2)
|
Min As†
(in2)
|
Reinforcement
Provided‡
|
As Prov.
for flexure (in2)
|
|
End Span
|
|
Column Strip
|
Exterior Negative
|
32.3
|
84
|
5.75
|
1.28
|
1.06
|
7-#4
|
1.4
|
|
Positive
|
26.5
|
84
|
5.75
|
1.04
|
1.06
|
6-#4
|
1.2
|
|
Interior Negative
|
50.3
|
84
|
5.75
|
2.02
|
1.06
|
11-#4
|
2.2
|
|
Middle Strip
|
Exterior Negative
|
0
|
84
|
5.75
|
0
|
1.06
|
6-#4
|
1.2
|
|
Positive
|
17.7
|
84
|
5.75
|
0.69
|
1.06
|
6-#4
|
1.2
|
|
Interior Negative
|
16.7
|
84
|
5.75
|
0.65
|
1.06
|
6-#4
|
1.2
|
|
Interior
Span
|
|
Column Strip
|
Positive
|
19.9
|
84
|
5.75
|
0.78
|
1.06
|
6-#4
|
1.2
|
|
Middle Strip
|
Positive
|
13.2
|
84
|
5.75
|
0.51
|
1.06
|
6-#4
|
1.2
|
b. Calculate additional slab reinforcement at columns
for moment transfer between slab and column by flexure
The
factored slab moment resisted by the column (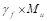 ) shall be assumed to be transferred by flexure.
Concentration of reinforcement over the column by closer spacing or additional
reinforcement shall be used to resist this moment. The fraction of slab moment
not calculated to be resisted by flexure shall be assumed to be resisted by
eccentricity of shear. ACI
318-14 (8.4.2.3)
) shall be assumed to be transferred by flexure.
Concentration of reinforcement over the column by closer spacing or additional
reinforcement shall be used to resist this moment. The fraction of slab moment
not calculated to be resisted by flexure shall be assumed to be resisted by
eccentricity of shear. ACI
318-14 (8.4.2.3)
Portion
of the unbalanced moment transferred by flexure is 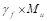 ACI 318-14 (8.4.2.3.1)
ACI 318-14 (8.4.2.3.1)
Where
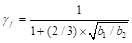 ACI
318-14 (8.4.2.3.2)
ACI
318-14 (8.4.2.3.2)
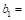 Dimension of the critical section
Dimension of the critical section 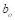 measured in the direction of the span for which
moments are determined in ACI 318, Chapter 8 (see Figure 5).
measured in the direction of the span for which
moments are determined in ACI 318, Chapter 8 (see Figure 5).
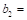 Dimension of the critical section
Dimension of the critical section 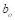 measured in the direction perpendicular to
measured in the direction perpendicular to 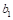 in ACI 318, Chapter 8 (see Figure 5).
in ACI 318, Chapter 8 (see Figure 5).
 = Effective slab width =
= Effective slab width = ACI 318-14 (8.4.2.3.3)
ACI 318-14 (8.4.2.3.3)
|
Table 8 -
Additional Slab Reinforcement required for moment transfer between slab and
column (EFM)
|
|
Span
Location
|
Mu*
(ft-kips)
|
γf
|
γf
Mu
(ft-kips)
|
Effective
slab
width, bb
(in.)
|
d
(in.)
|
As
req’d
within bb
(in2)
|
As
prov. For
flexure
within bb
(in2)
|
Add’l
Reinf.
|
|
End Span
|
|
Column Strip
|
Exterior
Negative
|
46.6
|
0.60
|
28.9
|
37
|
5.75
|
1.17
|
0.62
|
3-#4
|
|
Interior
Negative
|
7.8
|
0.60
|
4.7
|
37
|
5.75
|
0.18
|
0.97
|
-
|
|
*Mu is taken at the centerline
of the support in Equivalent Frame Method solution.
|
The
unbalanced moment from the slab-beams at the supports of the equivalent frame
are distributed to the support columns above and below the slab-beam in
proportion to the relative stiffness of the support columns. Referring to Figure
9, the unbalanced moment at joints 1 and 2 are:
Joint
1= +46.6 ft-kips
Joint
2= -84.0 + 76.2 = -7.8 ft-kips
The
stiffness and carry-over factors of the actual columns and the distribution of
the unbalanced slab moments (Msc) to the exterior and interior
columns are shown in Figure 10a.
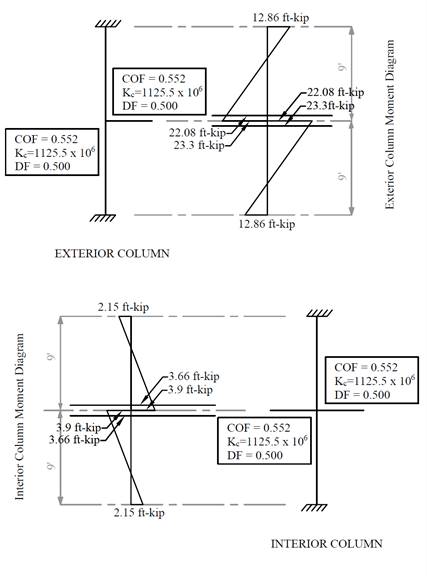
Figure 10a - Column Moments (Unbalanced Moments from
Slab-Beam)
In summary:
Mcol,Exterior= 22.08 ft-kips
Mcol,Interior = 3.66 ft-kips
The
moments determined above are combined with the factored axial loads (for each
story) and factored moments in the transverse direction for design of column
sections. Figure 10b shows the moment diagrams in the longitudinal and
transverse direction for the interior and exterior equivalent frames. Following
the previous procedure, the moment values at the face of interior, exterior,
and corner columns from the unbalanced moment values can be obtained. These
values are shown in the following table.
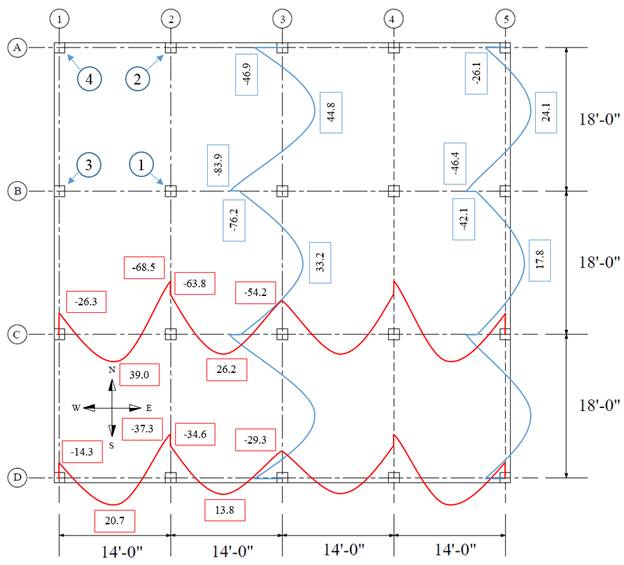
Figure 10b – Moment Diagrams (kips-ft)
|
Mu
kips-ft
|
Column number (See Figure
10b)
|
|
1
|
2
|
3
|
4
|
|
Mux
|
3.66
|
22.08
|
2.04
|
12.39
|
|
Muy
|
2.23
|
1.28
|
12.49
|
6.79
|
This section
includes the design of interior, edge, and corner columns using spColumn
software. The preliminary dimensions for these columns were calculated previously
in section one. The reduction of live load per ASCE 7-10
will be ignored in this example. However, the detailed procedure to calculate
the reduced live loads is explained in the “wide-Module Joist System”
example.
Interior Column (Column #1):
Assume 4 story building
Tributary area for
interior column is 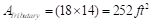
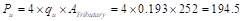 kips
kips
Mu,x = 3.66 ft-kips (see the previous Table)
Mu,y = 2.23 ft-kips
(see the previous Table)
Edge (Exterior) Column (Column #2):
Tributary area for
interior column is 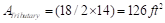
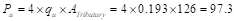 kips
kips
Mu,x = 22.08 ft-kips (see the previous Table)
Mu,y = 1.28 ft-kips
(see the previous Table)
Edge (Exterior) Column (Column #3):
Tributary area for
interior column is 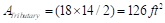
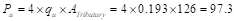 kips
kips
Mu,x = 2.04 ft-kips (see the previous Table)
Mu,y = 12.49 ft-kips
(see the previous Table)
Corner Column (Column #4):
Tributary area for
interior column is 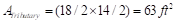
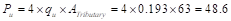 kips
kips
Mu,x = 12.39 ft-kips (see the previous Table)
Mu,y = 6.79 ft-kips
(see the previous Table)
The factored loads are then input into
spColumn to construct the axial load – moment interaction diagram.
Interior Column (Column #1):

Edge Column (Column #2):
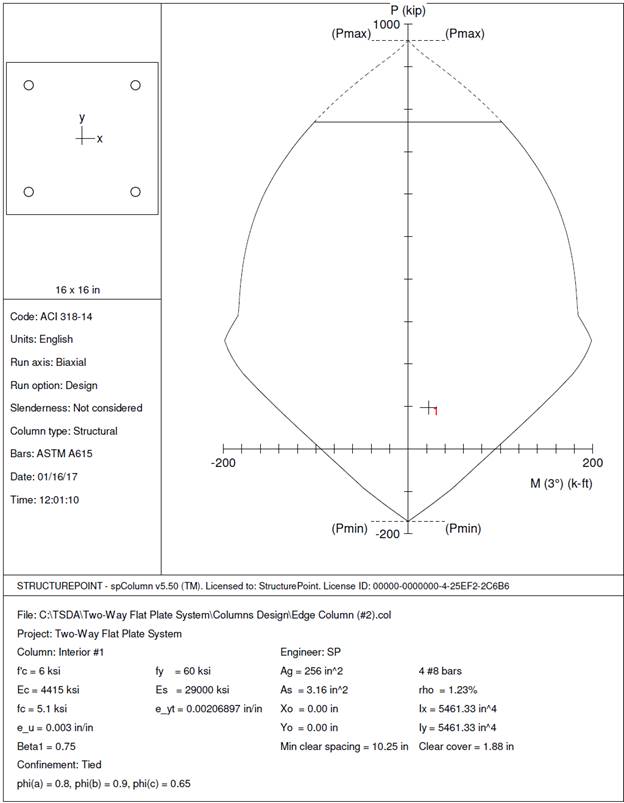
Edge Column (Column #3):
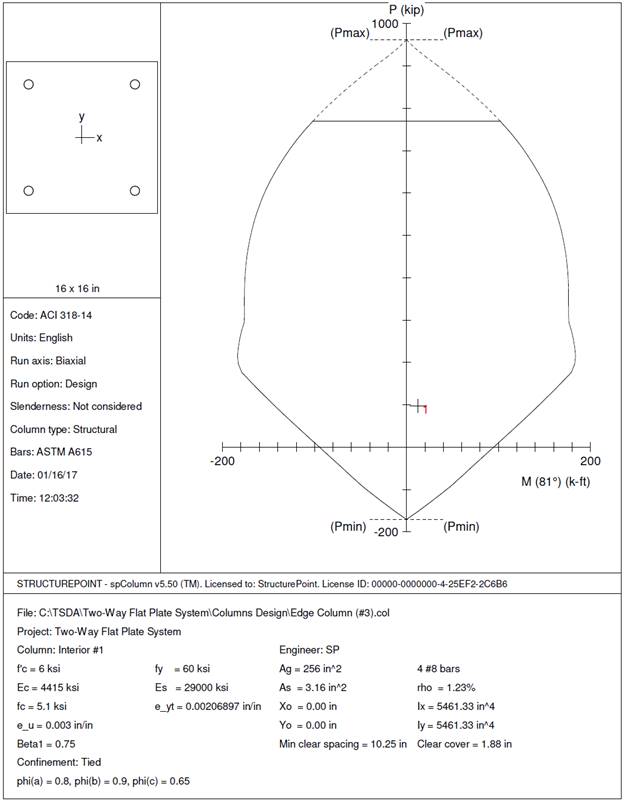
Corner Column (Column #4):

Shear strength of the slab in the vicinity
of columns/supports includes an evaluation of one-way shear (beam action) and
two-way shear (punching) in accordance with ACI 318 Chapter 22.
ACI 318-14 (22.5)
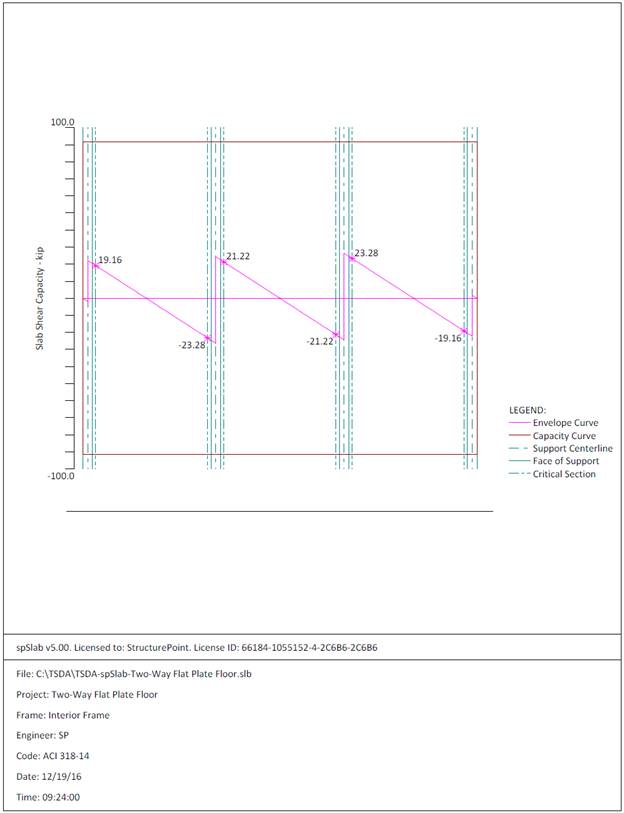
One-way
shear is critical at a distance d from the face of the column as shown in
Figure 3. Figure 11 shows the factored shear forces (Vu) at
the critical sections around each column. In members without shear
reinforcement, the design shear capacity of the section equals to the design
shear capacity of the concrete:
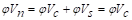 ,
, 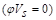 ACI 318-14 (Eq. 22.5.1.1)
ACI 318-14 (Eq. 22.5.1.1)
Where:
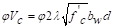 ACI 318-14 (Eq. 22.5.5.1)
ACI 318-14 (Eq. 22.5.5.1)
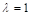 for normal weight concrete
for normal weight concrete
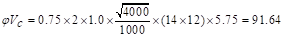 kips
kips
Because 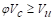 at all the critical sections, the slab has adequate
one-way shear strength.
at all the critical sections, the slab has adequate
one-way shear strength.
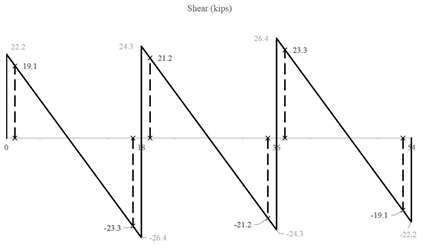
Figure 11 – One-way shear at critical sections (at
distance d from the face of the supporting column)
ACI 318-14 (22.6)
Two-way shear is critical on
a rectangular section located at d/2 away from the face of the column as shown
in Figure 5.
a. Exterior
column:
The factored shear force (Vu)
in the critical section is computed as the reaction at the centroid of the
critical section minus the self-weight and any superimposed surface dead and
live load acting within the critical section (d/2 away from column face).
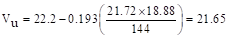 kips
kips
The factored unbalanced
moment used for shear transfer, Munb, is computed as the sum of the
joint moments to the left and right. Moment of the vertical reaction with
respect to the centroid of the critical section is also taken into account.
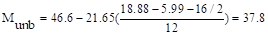 kips-ft
kips-ft
For the exterior column in
Figure 5, the location of the centroidal axis z-z is:
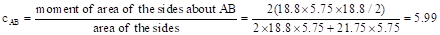 in.
in.
The polar moment Jc
of the shear perimeter is:
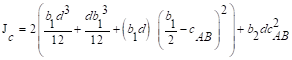
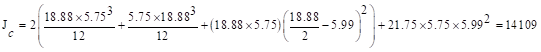 in.4
in.4
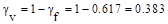 ACI 318-14 (Eq. 8.4.4.2.2)
ACI 318-14 (Eq. 8.4.4.2.2)
The length of the critical
perimeter for the exterior column:
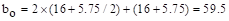 in.
in.
The two-way shear stress (vu)
can then be calculated as:
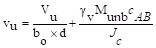 ACI 318-14 (R.8.4.4.2.3)
ACI 318-14 (R.8.4.4.2.3)
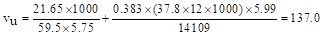 psi
psi
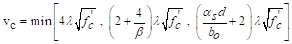 ACI 318-14 (Table 22.6.5.2)
ACI 318-14 (Table 22.6.5.2)
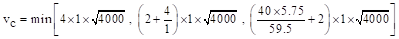
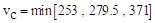 psi
psi 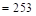 psi
psi
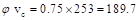 psi
psi
Since 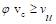 at
the critical section, the slab has adequate two-way shear strength at this
joint.
at
the critical section, the slab has adequate two-way shear strength at this
joint.
b. Interior
column:
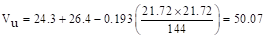 kips
kips
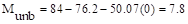 kips-ft
kips-ft
For the interior column in
Figure 5, the location of the centroidal axis z-z is:
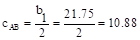 in.
in.
The polar moment Jc
of the shear perimeter is:
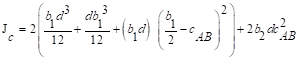
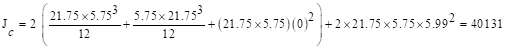 in.4
in.4
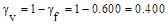 ACI 318-14 (Eq. 8.4.4.2.2)
ACI 318-14 (Eq. 8.4.4.2.2)
The length of the critical
perimeter for the interior column:
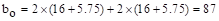 in.
in.
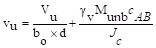 ACI 318-14 (R.8.4.4.2.3)
ACI 318-14 (R.8.4.4.2.3)
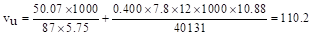 psi
psi
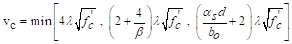 ACI 318-14 (Table 22.6.5.2)
ACI 318-14 (Table 22.6.5.2)
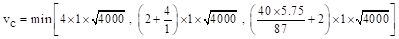
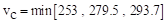 psi
psi 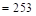 psi
psi
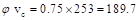 psi
psi
Since 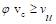 at
the critical section, the slab has adequate two-way shear strength at this
joint.
at
the critical section, the slab has adequate two-way shear strength at this
joint.
c. Corner
column:
In this
example, interior equivalent frame strip was selected where it only have
exterior and interior supports (no corner supports are included in this strip).
However, the two-way shear strength of corner supports usually governs. Thus,
the two-way shear strength for the corner column in this example will be
checked for educational purposes. Same procedure is used to find the reaction
and factored unbalanced moment used for shear transfer at the centroid of the critical
section for the corner support for the exterior equivalent frame strip.
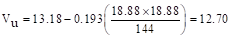 kips
kips
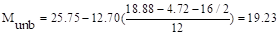 kips-ft
kips-ft
For the corner column in
Figure 5, the location of the centroidal axis z-z is:
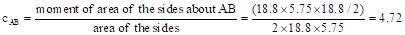 in.
in.
The polar moment Jc
of the shear perimeter is:
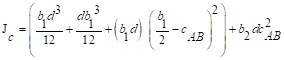
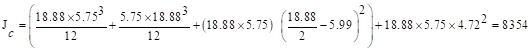 in.4
in.4
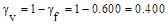 ACI
318-14 (Eq. 8.4.4.2.2)
ACI
318-14 (Eq. 8.4.4.2.2)
Where:
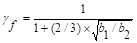 ACI 318-14 (8.4.2.3.2)
ACI 318-14 (8.4.2.3.2)
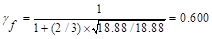
The length of the critical
perimeter for the exterior column:
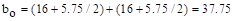 in.
in.
The two-way shear stress (vu)
can then be calculated as:
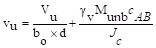 ACI 318-14 (R.8.4.4.2.3)
ACI 318-14 (R.8.4.4.2.3)
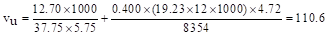 psi
psi
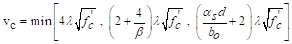 ACI 318-14 (Table 22.6.5.2)
ACI 318-14 (Table 22.6.5.2)
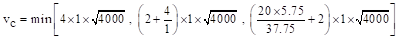
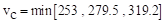 psi = 253 psi
psi = 253 psi
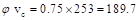 psi
psi
Since 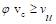 at
the critical section, the slab has adequate two-way shear strength at this
joint.
at
the critical section, the slab has adequate two-way shear strength at this
joint.
Since the slab
thickness was selected based on the minimum slab thickness tables in ACI
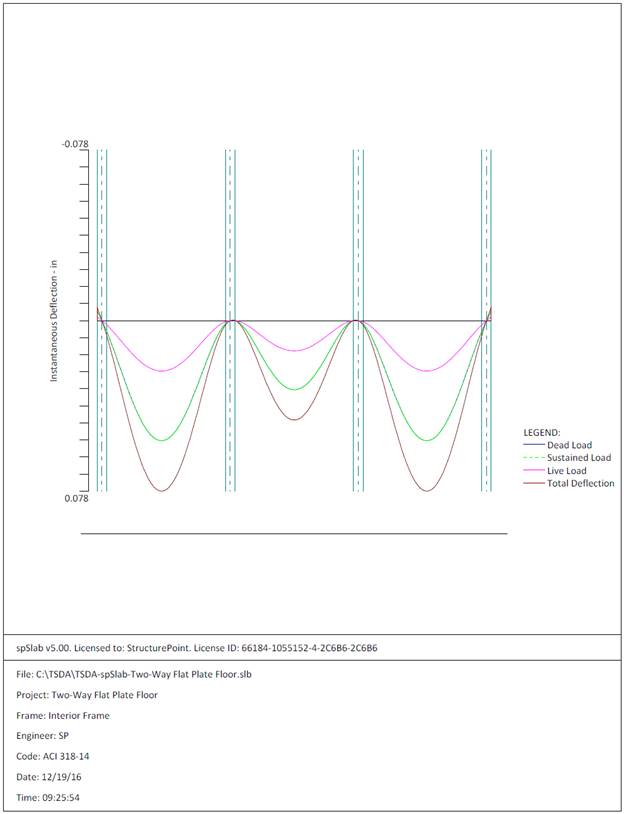
318-14, the deflection calculations are not required. However, the calculations
of immediate and time-dependent deflections are covered in this section for illustration
and comparison with spSlab model results.
The calculation of
deflections for two-way slabs is challenging even if linear elastic behavior
can be assumed. Elastic analysis for three service load levels (D, D + Lsustained,
D+LFull) is used to obtain immediate deflections of the two-way
slab in this example. However, other procedures may be used if they result in
predictions of deflection in reasonable agreement with the results of
comprehensive tests. ACI 318-14 (24.2.3)
The
effective moment of inertia (Ie) is used to account for the
cracking effect on the flexural stiffness of the slab. Ie for
uncracked section (Mcr > Ma) is equal to Ig.
When the section is cracked (Mcr < Ma), then
the following equation should be used:
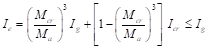 ACI 318-14 (Eq. 24.2.3.5a)
ACI 318-14 (Eq. 24.2.3.5a)
Where:
Ma = Maximum moment in member due to service loads at stage deflection is
calculated.
The
values of the maximum moments for the three service load levels are calculated
from structural analysis as shown previously in this document. These moments are
shown in Figure 12.
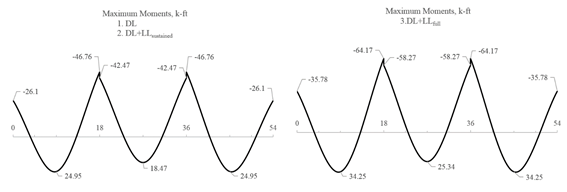
Figure 12 – Maximum Moments for the
Three Service Load Levels
Mcr = cracking moment.
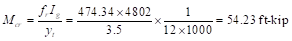 ACI
318-14 (Eq. 24.2.3.5b)
ACI
318-14 (Eq. 24.2.3.5b)
fr = Modulus of
rapture of concrete.
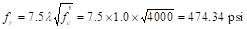 ACI
318-14 (Eq. 19.2.3.1)
ACI
318-14 (Eq. 19.2.3.1)
Ig = Moment of inertia of the gross uncracked concrete
section
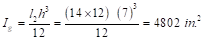
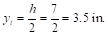
Icr
= moment of inertia of the cracked section
transformed to concrete. PCA Notes on ACI 318-11 (9.5.2.2)
The
calculations shown below are for the design strip (frame strip). The values of
these parameters for column and middle strips are shown in Table 9.
As
calculated previously, the exterior span frame strip near the interior support is
reinforced with 17 #4 bars located at 1.25 in. along the section from the top
of the slab. Figure 13 shows all the parameters needed to calculate the moment
of inertia of the cracked section transformed to concrete.

Figure 13 – Cracked Transformed
Section
Ecs = Modulus of elasticity of slab
concrete.
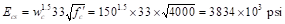 ACI
318-14 (19.2.2.1.a)
ACI
318-14 (19.2.2.1.a)
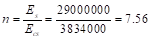 PCA Notes on ACI 318-11 (Table 10-2)
PCA Notes on ACI 318-11 (Table 10-2)
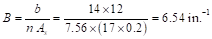 PCA Notes on ACI 318-11 (Table 10-2)
PCA Notes on ACI 318-11 (Table 10-2)
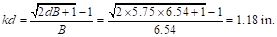 PCA Notes on
ACI 318-11 (Table 10-2)
PCA Notes on
ACI 318-11 (Table 10-2)
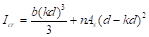 PCA
Notes on ACI 318-11 (Table 10-2)
PCA
Notes on ACI 318-11 (Table 10-2)
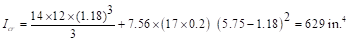
The effective moment of inertia procedure described in
the Code is considered sufficiently accurate to estimate deflections. The
effective moment of inertia, Ie, was developed to provide a
transition between the upper and lower bounds of Ig and Icr
as a function of the ratio Mcr/Ma. For conventionally
reinforced (nonprestressed) members, the effective moment of inertia, Ie, shall
be calculated by Eq. (24.2.3.5a) unless obtained by a more comprehensive
analysis.
Ie shall be permitted to be
taken as the value obtained from Eq. (24.2.3.5a) at midspan for simple and
continuous spans, and at the support for cantilevers. ACI
318-14 (24.2.3.7)
For continuous one-way slabs
and beams. Ie shall be permitted to be taken as the average of values
obtained from Eq. (24.2.3.5a) for the critical positive and negative moment
sections. ACI 318-14 (24.2.3.6)
For the exterior span
(span with one end continuous) with service load level (D+LLfull):
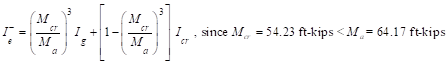
ACI
318-14 (24.2.3.5a)
Where
Ie- is the effective moment of inertia for the
critical negative moment section (near the support).
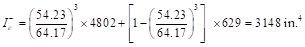
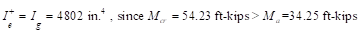
Where
Ie+ is
the effective moment of inertia for the critical positive moment section
(midspan).
Since midspan stiffness
(including the effect of cracking) has a dominant effect on deflections,
midspan section is heavily represented in calculation of Ie and this
is considered satisfactory in approximate deflection calculations. The averaged effective moment of inertia (Ie,avg)
is given by:
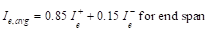 PCA
Notes on ACI 318-11 (9.5.2.4(1))
PCA
Notes on ACI 318-11 (9.5.2.4(1))
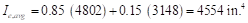
Where:
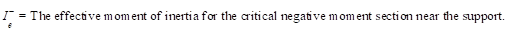
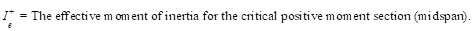
For the interior span (span
with both ends continuous) with service load level (D+LLfull):
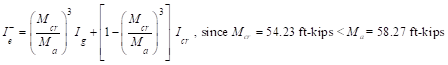
ACI
318-14 (24.2.3.5a)
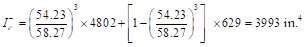
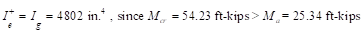
The averaged effective
moment of inertia (Ie,avg) is given by:
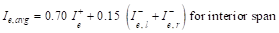 PCA Notes on ACI 318-11 (9.5.2.4(2))
PCA Notes on ACI 318-11 (9.5.2.4(2))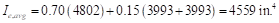
Where:
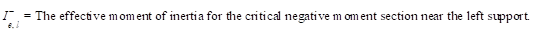
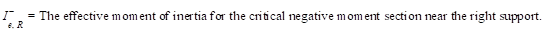
Table 9
provides a summary of the required parameters and calculated values needed for
deflections for exterior and interior equivalent frame. It also provides a
summary of the same values for column strip and middle strip to facilitate
calculation of panel deflection.
|
Table 9 –
Averaged Effective Moment of Inertia Calculations
|
|
For Frame
Strip
|
|
Span
|
zone
|
Ig,
in.4
|
Icr,
in.4
|
Ma,
ft-kip
|
Mcr,
k-ft
|
Ie,
in.4
|
Ie,avg,
in.4
|
|
D
|
D +
LLSus
|
D +
Lfull
|
D
|
D +
LLSus
|
D +
Lfull
|
D
|
D +
LLSus
|
D +
Lfull
|
|
Ext
|
Left
|
4802
|
499
|
-26.10
|
-26.10
|
-35.78
|
54.23
|
4802
|
4802
|
4802
|
4802
|
4802
|
4554
|
|
Midspan
|
465
|
24.95
|
24.95
|
34.25
|
4802
|
4802
|
4802
|
|
Right
|
629
|
-46.76
|
-46.76
|
-64.17
|
4802
|
4802
|
3148
|
|
Int
|
Left
|
629
|
-42.47
|
-42.47
|
-58.27
|
4802
|
4802
|
3993
|
4802
|
4802
|
4559
|
|
Mid
|
465
|
18.47
|
18.47
|
25.34
|
4802
|
4802
|
4802
|
|
Right
|
629
|
-42.47
|
-42.47
|
-58.27
|
4802
|
4802
|
3993
|
Deflections in two-way slab systems shall be
calculated taking into account size and shape of the panel, conditions of
support, and nature of restraints at the panel edges. For immediate deflections
two-way slab systems the midpanel deflection
is computed as the sum of deflection at midspan of the column strip or column
line in one direction (Δcx or Δcy)
and deflection at midspan of the middle strip in the orthogonal direction (Δmx
or Δmy). Figure 14 shows the deflection computation for
a rectangular panel. The average Δ for panels that have different
properties in the two direction is calculated as follows:
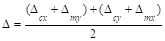 PCA
Notes on ACI 318-11 (9.5.3.4 Eq. 8)
PCA
Notes on ACI 318-11 (9.5.3.4 Eq. 8)
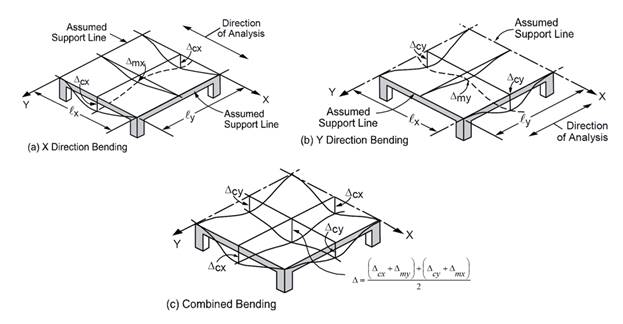
Figure 14 – Deflection Computation
for a rectangular Panel
To
calculate each term of the previous equation, the following procedure should be
used. Figure 15 shows the procedure of calculating the term Δcx.
same procedure can be used to find the other terms.
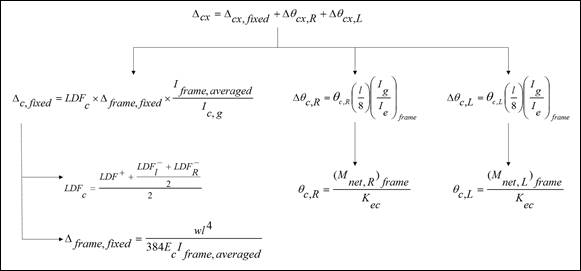
Figure 15 –Δcx calculation
procedure
For exterior span - service
dead load case:
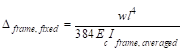 PCA
Notes on ACI 318-11 (9.5.3.4 Eq. 10)
PCA
Notes on ACI 318-11 (9.5.3.4 Eq. 10)
Where:

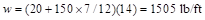
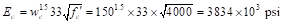 ACI
318-14 (19.2.2.1.a)
ACI
318-14 (19.2.2.1.a)
Iframe,averaged =
The averaged effective moment of inertia (Ie,avg)
for the frame strip for service dead load case from Table 9 = 4802 in.4
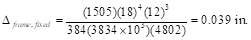
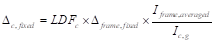 PCA
Notes on ACI 318-11 (9.5.3.4 Eq. 11)
PCA
Notes on ACI 318-11 (9.5.3.4 Eq. 11)
Where LDFc
is the load distribution factor for the column strip. The load distribution
factor for the column strip can be found from the following equation:
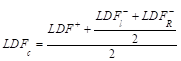
And the load distribution
factor for the middle strip can be found from the following equation:
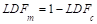
For the
end span, LDF for exterior negative region (LDFL¯), interior
negative region (LDFR¯), and positive region (LDFL+) are 1.00, 0.75, and 0.60, respectively (From Table 6 of this document).
Thus, the load distribution factor for the column strip for the end span is
given by:
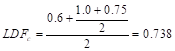
Ic,g
= The gross moment of inertia (Ig)
for the column strip for service dead load = 2401 in.4
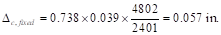
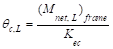 PCA
Notes on ACI 318-11 (9.5.3.4 Eq. 12)
PCA
Notes on ACI 318-11 (9.5.3.4 Eq. 12)
Where:
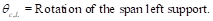
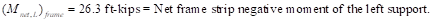
Kec = effective column stiffness =
553.7 x 106 in.-lb (calculated
previously).
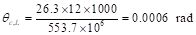
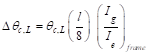 PCA
Notes on ACI 318-11 (9.5.3.4 Eq. 14)
PCA
Notes on ACI 318-11 (9.5.3.4 Eq. 14)
Where:
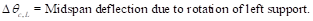
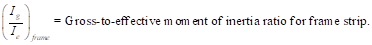
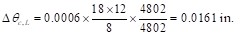
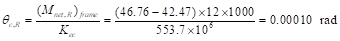
Where
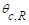 =
rotation of the span right support.
=
rotation of the span right support.
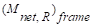 =
Net frame strip negative moment of the right support.
=
Net frame strip negative moment of the right support.
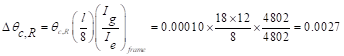 in.
in.
Where:
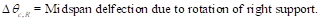
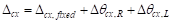 PCA
Notes on ACI 318-11 (9.5.3.4 Eq. 9)
PCA
Notes on ACI 318-11 (9.5.3.4 Eq. 9)
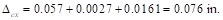
Following
the same procedure, Δmx can be calculated for the middle
strip. This procedure is repeated for the equivalent frame in the orthogonal
direction to obtain Δcy, and Δmy
for the end and middle spans for the other load levels (D+LLsus
and D+LLfull).
Assuming
square panel, Δcx = Δcy=
0.076 in. and Δmx = Δmy=
0.039 in.
The average Δ for the corner panel is
calculated as follows: