Interaction Diagram - Tied Reinforced Concrete Column (Using CSA A23.3-14)

Interaction Diagram - Tied Reinforced Concrete Column

Develop an interaction diagram for the square tied concrete column shown in the figure below about the x-axis using CSA A23.3-14 provisions. Determine six control points on the interaction diagram and compare the calculated values in the Reference and with exact values from the complete interaction diagram generated by spColumn engineering software program from StructurePoint.

Figure 1 – Reinforced Concrete Column Cross-Section

Contents

1. Pure Compression. 3

1.1. Nominal axial resistance at zero eccentricity. 3

1.2. Factored axial load resistance at zero eccentricity. 3

1.3. Maximum factored axial load resistance. 3

2. Bar Stress Near Tension Face of Member Equal to Zero, ( ε_s = f_s = 0 ) 4

2.1. c, a, and strains in the reinforcement 4

2.2. Forces in the concrete and steel 4

2.3. P_r and M_r 5

3. Bar Stress Near Tension Face of Member Equal to 0.5 f_y, ( f_s = - 0.5 f_y ) 6

3.1. c, a, and strains in the reinforcement 6

3.2. Forces in the concrete and steel 6

3.3. P_r and M_r 7

4. Bar Stress Near Tension Face of Member Equal to f_y, ( f_s = - f_y ) 8

4.1. c, a, and strains in the reinforcement 8

4.2. Forces in the concrete and steel 9

4.3. P_r and M_r 9

5. Pure Bending. 10

5.1. c, a, and strains in the reinforcement 10

5.2. Forces in the concrete and steel 10

5.3. P_r and M_r 11

6. Pure Tension. 12

6.1. Strength under pure axial tension (P_rt) 12

6.2. Corresponding Moment (M_rt) 12

7. Column Interaction Diagram - spColumn Software. 13

8. Summary and Comparison of Design Results. 19

9. Conclusions & Observations. 20

Code

Design of Concrete Structures (CSA A23.3-14)

Reference

Reinforced Concrete Mechanics and Design, 1^st Canadian Edition, 2000, James MacGregor and Fred Michael Bratlett, Prentice Hall Canada Inc.

Design Data

f_c’ = 35 MPa

f_y = 400 MPa

Cover = 55 mm to the center of the reinforcement

Column 400 mm x 400 mm

Top reinforcement = 4 No. 30

Bottom reinforcement = 4 No. 30

Solution

Use the traditional hand calculations approach to generate the interaction diagram for the concrete column section shown above by determining the following six control points:

Point 1: Pure compression

Point 2: Bar stress near tension face of member equal to zero, ( f_s = 0 )

Point 3: Bar stress near tension face of member equal to 0.5 f_y ( f_s = - 0.5 f_y )

Point 4: Bar stress near tension face of member equal to f_y ( f_s = - f_y )

Point 5: Pure bending 

Point 6: Pure tension

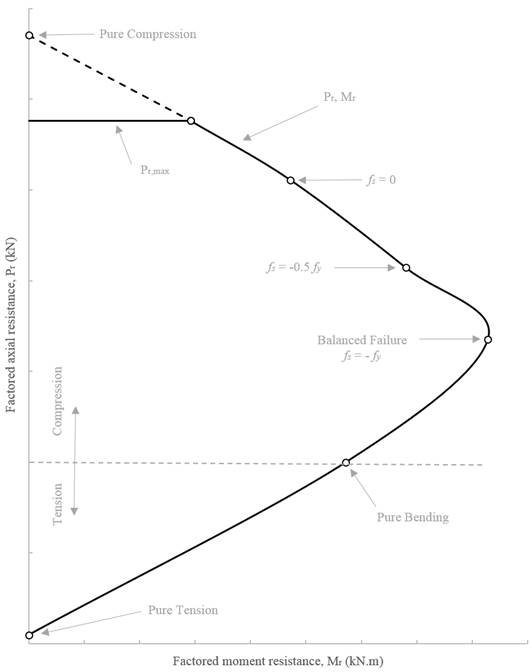
Figure 2 – Control Points

1. Pure Compression

1.1. Nominal axial resistance at zero eccentricity

CSA A23.3-14 (Equation 10.1)

1.2. Factored axial load resistance at zero eccentricity

Since this column is a tied column with steel strain in compression:

CSA A23.3-14 (Equation 10.11)

Where:

CSA A23.3-14 (8.4.2)

CSA A23.3-14 (8.4.3(a))

1.3. Maximum factored axial load resistance

CSA A23.3-14 (Equation 10.9)

2. Bar Stress Near Tension Face of Member Equal to Zero, ( ε_s = f_s = 0 )

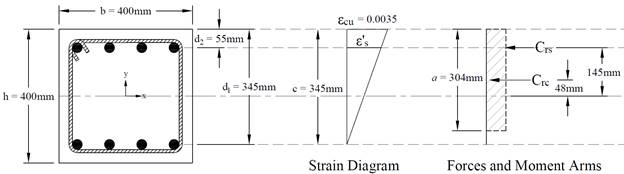
Figure 3 – Strains, Forces, and Moment Arms (ε_t = f_s = 0)

Strain ε_s is zero in the extreme layer of tension steel. This case is considered when calculating an interaction diagram because it marks the change from compression lap splices being allowed on all longitudinal bars, to the more severe requirement of tensile lap splices. CSA A23.3-14 (12.15 and 16)

2.1. c, a, and strains in the reinforcement

Where c is depth of the neutral axis measured from the compression edge of the column section.

CSA A23.3-14 (3.2)

CSA A23.3-14 (10.1.7)

Where:

a = Depth of equivalent rectangular stress block                                                                         CSA A23.3-14 (3.2)

CSA A23.3-14 (Equation 10.2)

CSA A23.3-14 (8.4.2)

CSA A23.3-14 (8.4.3(a))

CSA A23.3-14 (10.1.3)

2.2. Forces in the concrete and steel

CSA A23.3-14 (10.1.7)

The area of the reinforcement in this layer has been included in the area (ab) used to compute C_c. As a result, it is necessary to subtract α₁ϕ_cf_c’ from ϕ_sf_s’ before computing C_rs:

2.3. P_r and M_r

3. Bar Stress Near Tension Face of Member Equal to 0.5 f_y, ( f_s = - 0.5 f_y )

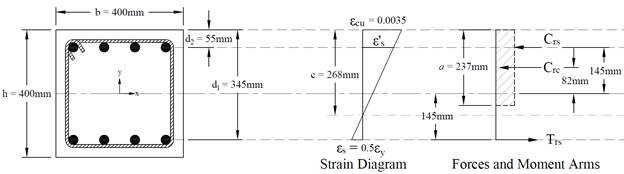
Figure 4 – Strains, Forces, and Moment Arms (f_s = - 0.5 f_y)

3.1. c, a, and strains in the reinforcement

CSA A23.3-14 (8.4.2)

CSA A23.3-14 (8.4.3(a))

CSA A23.3-14 (10.1.3)

Where c is depth of the neutral axis measured from the compression edge of the column section.

CSA A23.3-14 (3.2)

CSA A23.3-14 (10.1.7)

Where:

a = Depth of equivalent rectangular stress block                                                                         CSA A23.3-14 (3.2)

CSA A23.3-14 (Equation 10.2)

3.2. Forces in the concrete and steel

CSA A23.3-14 (10.1.7)

The area of the reinforcement in this layer has been included in the area (ab) used to compute C_c. As a result, it is necessary to subtract α₁ϕ_cf_c’ from ϕ_sf_s’ before computing C_rs:

3.3. P_r and M_r

4. Bar Stress Near Tension Face of Member Equal to f_y, ( f_s = - f_y )

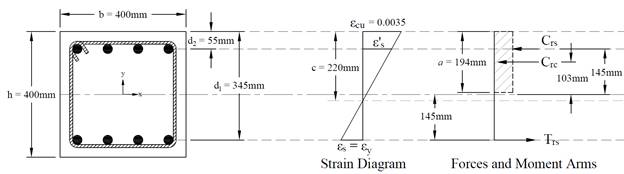
Figure 5 – Strains, Forces, and Moment Arms (f_s = - f_y)

This strain distribution is called the balanced failure case and the compression-controlled strain limit. It marks the change from compression failures originating by crushing of the compression surface of the section, to tension failures initiated by yield of longitudinal reinforcement.

4.1. c, a, and strains in the reinforcement

CSA A23.3-14 (8.4.2)

CSA A23.3-14 (8.4.3(a))

CSA A23.3-14 (10.1.3)

Where c is depth of the neutral axis measured from the compression edge of the column section.

CSA A23.3-14 (3.2)

CSA A23.3-14 (10.1.7)

Where:

a = Depth of equivalent rectangular stress block                                                                         CSA A23.3-14 (3.2)

CSA A23.3-14 (Equation 10.2)

4.2. Forces in the concrete and steel

CSA A23.3-14 (10.1.7)

The area of the reinforcement in this layer has been included in the area (ab) used to compute C_c. As a result, it is necessary to subtract α₁ϕ_cf_c’ from ϕ_sf_s’ before computing C_rs:

4.3. P_r and M_r

5. Pure Bending

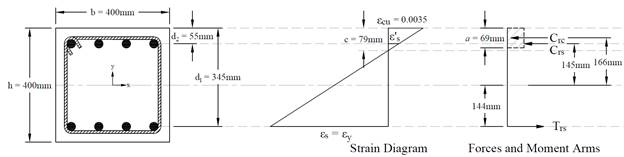
Figure 6 – Strains, Forces, and Moment Arms (Pure Moment)

This corresponds to the case where the factored axial load resistance, P_r, is equal to zero. Iterative procedure is used to determine the factored moment resistance as follows:

5.1. c, a, and strains in the reinforcement

Where c is depth of the neutral axis measured from the compression edge of the column section.

CSA A23.3-14 (3.2)

CSA A23.3-14 (10.1.7)

Where:

CSA A23.3-14 (Equation 10.2)

CSA A23.3-14 (10.1.3)

CSA A23.3-14 (8.4.2)

CSA A23.3-14 (8.4.3(a))

5.2. Forces in the concrete and steel

CSA A23.3-14 (10.1.7)

The area of the reinforcement in this layer has been included in the area (ab) used to compute C_c. As a result, it is necessary to subtract α₁ϕ_cf_c’ from ϕ_sf_s’ before computing C_rs:

5.3. P_r and M_r

The assumption that c = 78.55 mm is correct

6. Pure Tension

The final loading case to be considered is concentric axial tension. The strength under pure axial tension is computed by assuming that the section is completely cracked through and subjected to a uniform strain greater than or equal to the yield strain in tension. The strength under such a loading is equal to the yield strength of the reinforcement in tension.

6.1. Strength under pure axial tension (P_rt)

6.2. Corresponding Moment (M_rt)

Since the section is symmetrical

7. Column Interaction Diagram - spColumn Software

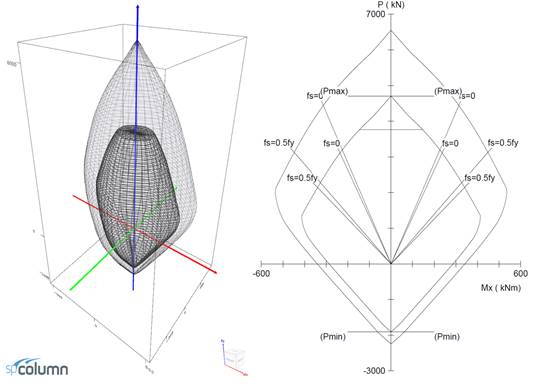
spColumn program performs the analysis of the reinforced concrete section conforming to the provisions of the Strength Design Method and Unified Design Provisions with all conditions of strength satisfying the applicable conditions of equilibrium and strain compatibility. For this column section, we ran in investigation mode with control points using the CSA A23.3-14. In lieu of using program shortcuts, spSection (Figure 9) was used to place the reinforcement and define the cover to illustrate handling of irregular shapes and unusual bar arrangement.

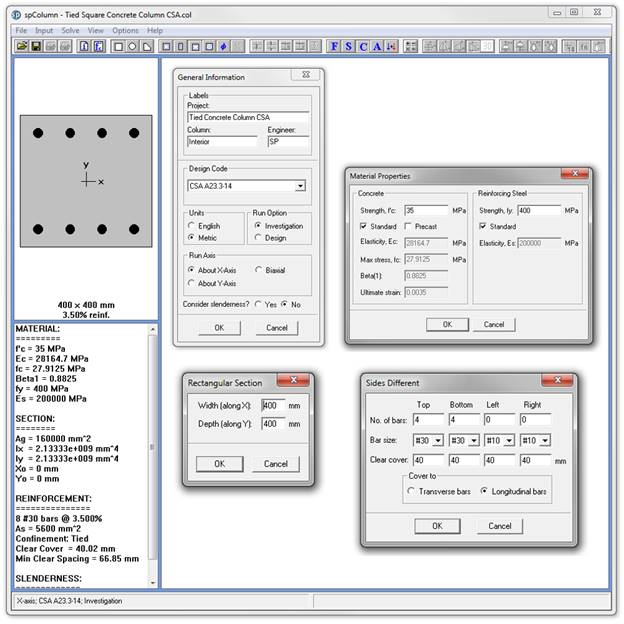
Figure 7 – Generating spColumn Model

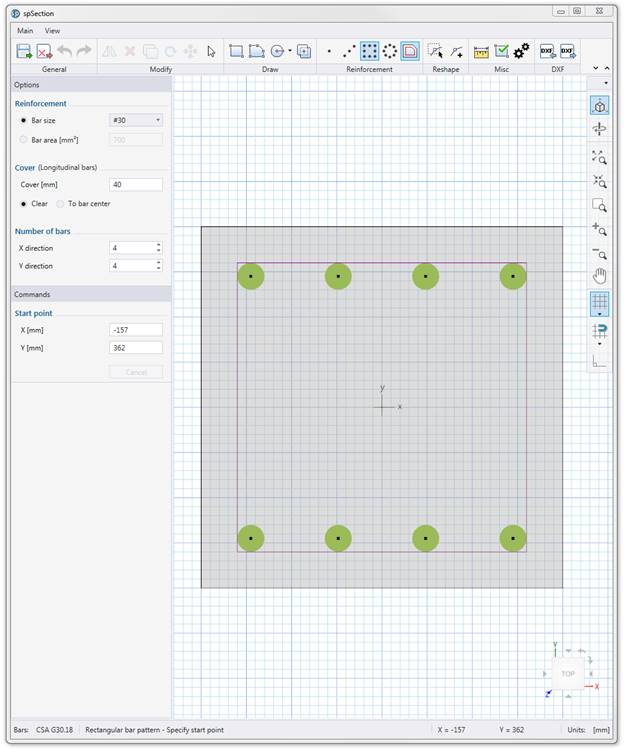
Figure 8 – spColumn Model Editor (spSection)

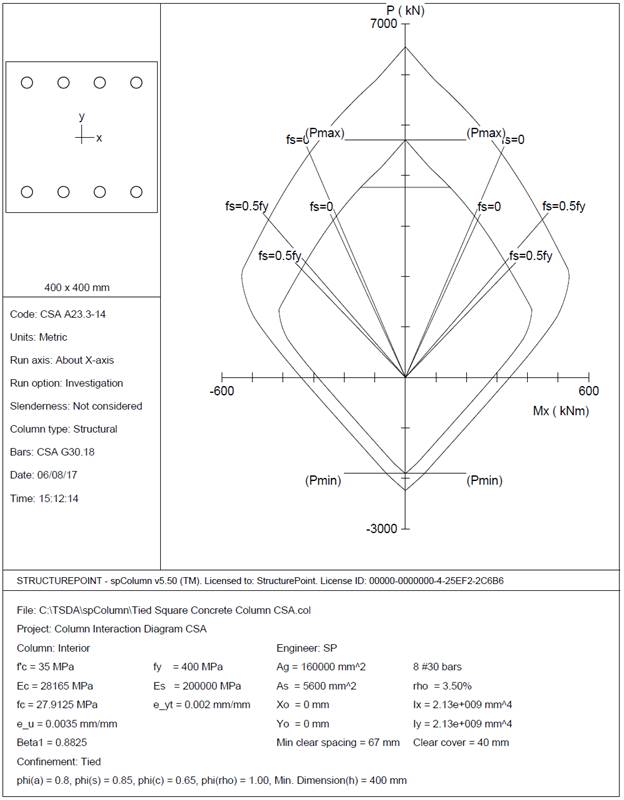
Figure 9 – Column Section Interaction Diagram about the X-Axis (spColumn)

8. Summary and Comparison of Design Results

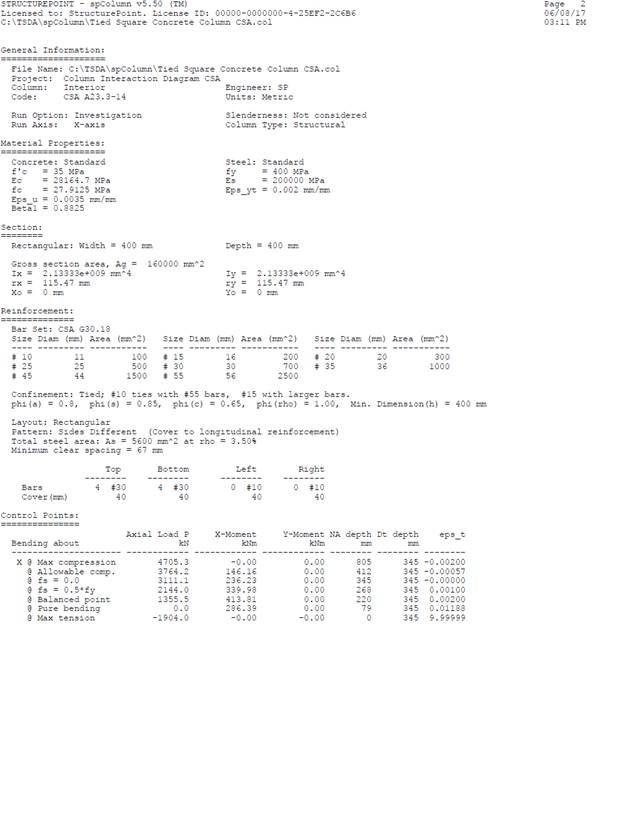
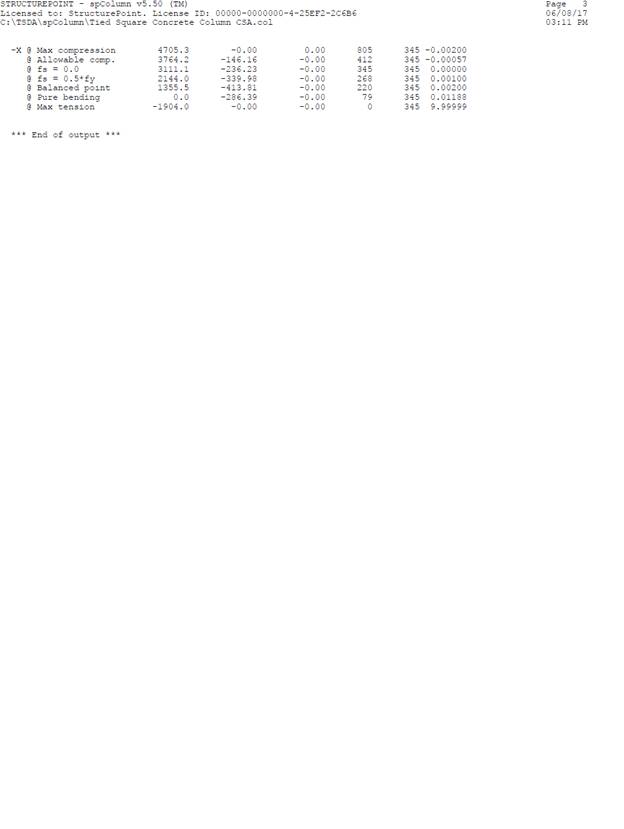
Table 1 - Comparison of Results
Support	Pr, kN			Mr, kN.m
	Hand	Reference^*^**	spColumn	Hand	Reference^* **	spColumn
Max compression	4705	4490	4705	0	0	0
Allowable compression	3764	3592	3764	---	---	---
fs = 0.0	3111	2945	3111	236	229	236
fs = 0.5 fy	2144	2015	2144	340	330	340
Balanced point	1355	1253	1355	414	403	414
Pure bending	0	0	0	286	285	286
Max tension	1904	1904	1904	0	0	0
^* Reinforced Concrete Mechanic and Design, 1^st Canadian Edition, James MacGregor and Fred Bartlett – Example 11-1 **  The reference used CSA A23.3-94 where the resistance factor for concrete (ϕc) is 0.60. The hand calculation and spColumn used CSA A23.3-14 where the resistance factor for concrete (ϕc) is 0.65. (Check Column Interaction Diagram Using CSA A23.3-94 Example)

9. Conclusions & Observations

The analysis of the reinforced concrete section performed by spColumn conforms to the provisions of the Strength Design Method and Unified Design Provisions with all conditions of strength satisfying the applicable conditions of equilibrium and strain compatibility.

In the calculation shown above a P-M interaction diagram was generated with moments about the X-Axis (Uniaxial bending). Since the reinforcement in the section is not symmetrical, a different P-M interaction diagram is needed for the other orthogonal direction about the Y-Axis (See the following Figure for the case where f_s = f_y).

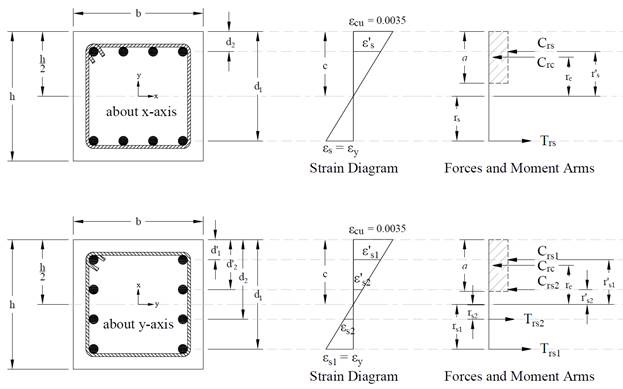
Figure 10 – Strains, Forces, and Moment Arms (f_s = - f_y Moments About x- and y-axis)

When running about the Y-Axis, we have 2 bars in 4 layers instead of 4 bars in just 2 layers (about X-Axis) resulting in a completely different interaction diagram as shown in the following Figure.

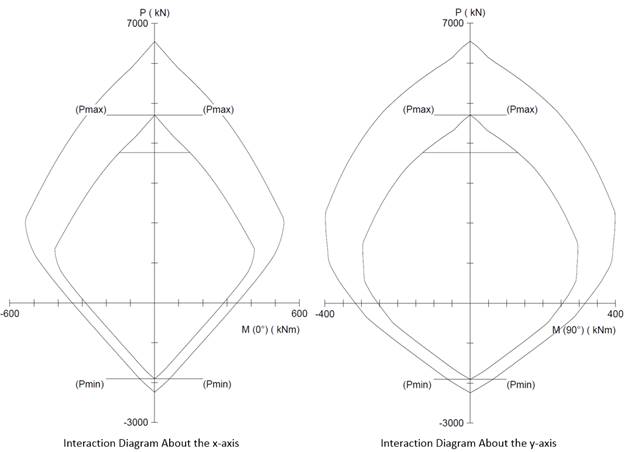
Figure 11 – Comparison of Column Interaction Diagrams about X-Axis and Y-Axis (spColumn)

Further differences in the interaction diagram in both directions can result if the column cross section geometry is irregular.

In most building design calculations, such as the examples shown for flat plate or flat slab concrete floor systems, all building columns are subjected to M_x and M_y due to lateral forces and unbalanced moments from both directions of analysis. This requires an evaluation of the column P-M interaction diagram in two directions simultaneously (biaxial bending).

StucturePoint’s spColumn program can also evaluate column sections in biaxial mode to produce the results shown in the following Figure for the column section in this example.

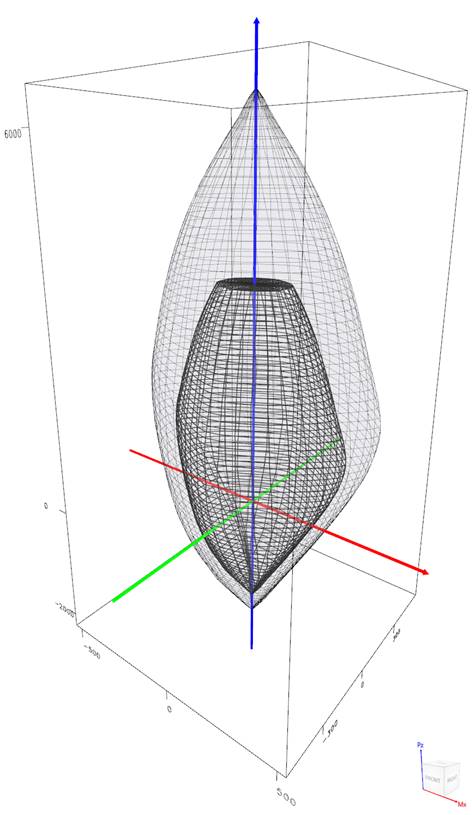
Figure 12 – Nominal & Design Interaction Diagram in Two Directions (Biaxial) (spColumn)