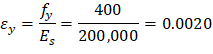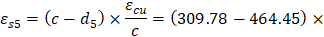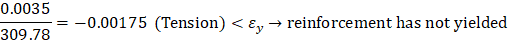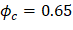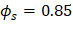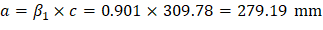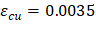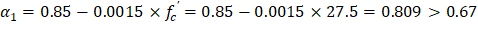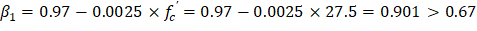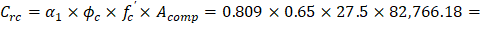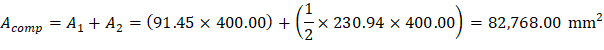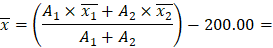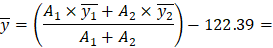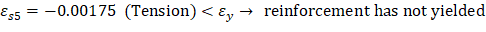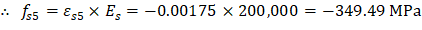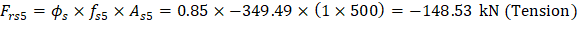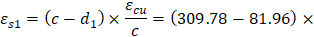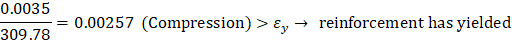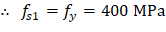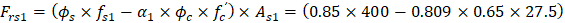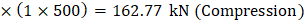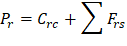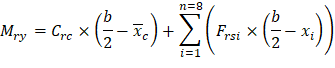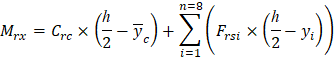1. Concrete Column Biaxial Resistance Calculations
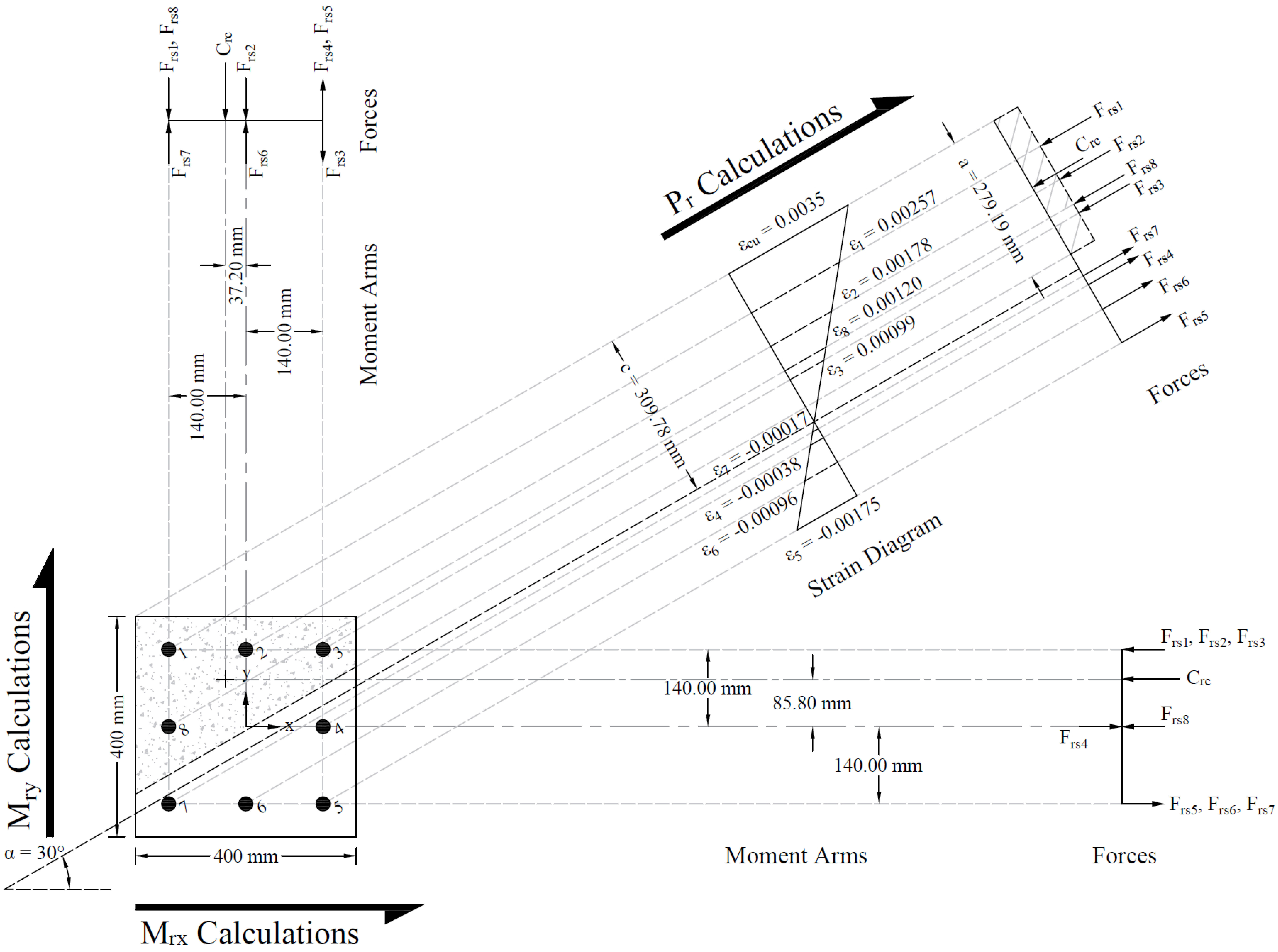
Figure 4 - Strains, Forces, and Moment Arms Diagram
1.1. Location of Neutral Axis and Concrete Compression Force
The trial-and-error process for calculating the neutral axis depth and angle α is not required in this example since these values are given (c = 309.78 mm and α = 30.0o). Where c is the distance from the fiber of maximum compressive strain to the neutral axis and α is the angle of the neutral axis.
CSA A23.3-19 (3.2)
| |
| |
| CSA A23.3-19 (8.4.2) |
| CSA A23.3-19 (8.4.3(a)) |
| CSA A23.3-19 (10.1.7) |
| CSA A23.3-19 (10.1.3) |
Where: | |
a = Depth of equivalent rectangular stress block | |
| CSA A23.3-19 (Equation 10.1) |
| CSA A23.3-19 (Equation 10.2) |
| CSA A23.3-19 (10.1.7) |
Where (see the following figure): | |
| |
| |
| |
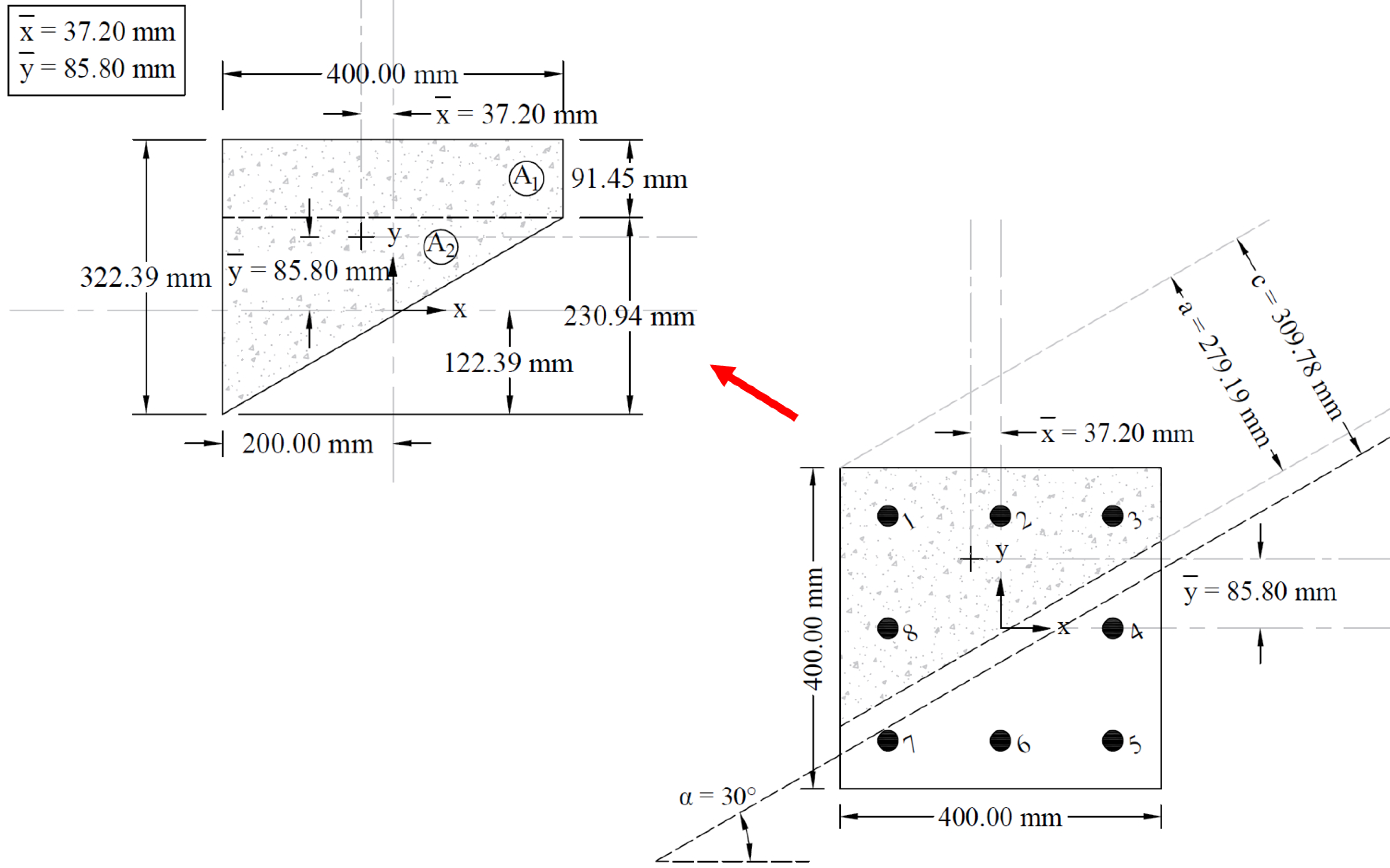
Figure 5 - Cracked Concrete Column Section Centroid Calculations
1.2. Strains and Forces Determination in Reinforcement Layers
The following shows the calculations of forces in the reinforcement layers with the extreme tension (at bar 5) and extreme compression (at bar 1) strains. The calculations for the rest of layers are shown the table at the end of this section.
For extreme tension reinforcement layer (at bar 5): | |
| |
| |
| |
For extreme compression reinforcement layer (at bar 1): | |
| |
| |
The area of the reinforcement in this layer is included in the area used to compute Crc (a = 279.19 mm > d1 = 81.96 mm). As a result, it is necessary to subtract α1ϕcfc’ from ϕsfs1 before computing Frs1: | |
| |
The same procedure shown above can be repeated to calculate the forces in the remaining reinforcement locations, results are summarized in the following table: | |
Table 1 - Strains, internal force resultants and Moments | |||||||||
Location | d, mm | ε, mm/mm | fs, MPa | Frs, kN | Crc, kN | Moment arm (x), mm | Mry, kN-m | Moment arm (y), mm | Mrx, kN-m |
Concrete | --- | 0.00350 | --- | --- | 1196.53 | 37.20 | 44.52 | 85.80 | 102.66 |
Bar 1 | 81.962 | 0.00257 | 400.00 | 162.77* | --- | 140.00 | 22.79 | 140.00 | 22.79 |
Bar 2 | 151.962 | 0.00178 | 356.62 | 144.34* | --- | 0.00 | 0.00 | 140.00 | 20.21 |
Bar 3 | 221.962 | 0.00099 | 198.45 | 77.11* | --- | -140.00 | -10.80 | 140.00 | 10.80 |
Bar 4 | 343.205 | -0.00038 | -75.52 | -32.1 | --- | -140.00 | 4.49 | 0.00 | 0.00 |
Bar 5 | 464.449 | -0.00175 | -349.49 | -148.53 | --- | -140.00 | 20.79 | -140.00 | 20.79 |
Bar 6 | 394.449 | -0.00096 | -191.31 | -81.31 | --- | 0.00 | 0.00 | -140.00 | 11.38 |
Bar 7 | 324.449 | -0.00017 | -33.14 | -14.08 | --- | 140.00 | -1.97 | -140.00 | 1.97 |
Bar 8 | 203.205 | 0.00120 | 240.83 | 95.12* | --- | 140.00 | 13.32 | 0.00 | 0.00 |
Axial Load and Biaxial Bending Moments Resistance | Pr, kN | 1399.85 | Mry, kN-m | 93.14 | Mrx, kN-m | 190.60 | |||
* The area of the reinforcement in this layer has been included in the area used to compute Crc. As a result, α1ϕcfc’ is subtracted from ϕsfs in the computation of Frs. | |||||||||
1.3. Calculation of Pr, Mrx and Mry