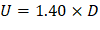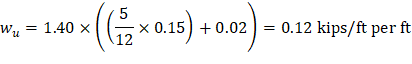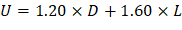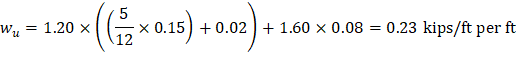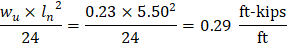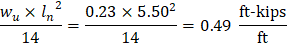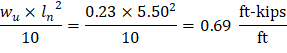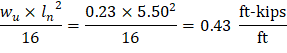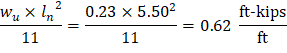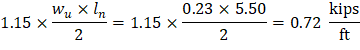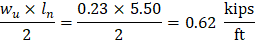2. Design of Structural Members
The design of the following structural members is performed and compared with results of the engineering software program spBeam:
2.1. One-Way Slab
2.2. One-Way Joist
2.3. Interior Beam
2.4. Exterior Beam
2.5. Interior Column
A unit strip of 1 ft is considered for the design of slab spanning between ribs. Note that ACI 318-14 does not allow live load reduction for one-way slabs.
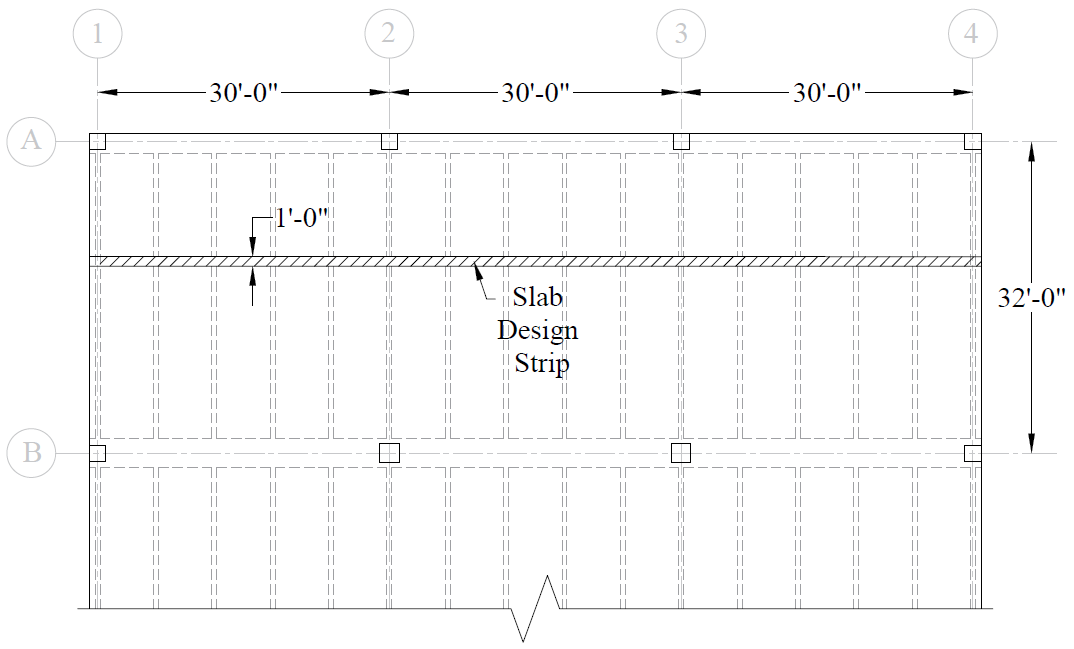
Figure 3 – Partial Plan View Illustrating Slab Design Strip
Slab design involves the following steps:
2.1.1. Determination of span loads
2.1.2. Determination of design moments and shears
2.1.3. Flexural Design
2.1.4. Shear Design
2.1.5. Deflections
2.1.6. Computer Program Solution
2.1.7. Summary and comparison of design results
2.1.8. Conclusions and observations
2.1.1. Determination of span loads
The following gravity load combinations are considered: | |
| ACI 318-14 (Eq. 5.3.1a) |
| |
| ACI 318-14 (Eq. 5.3.1b) |
| |
Span loads are governed by the second load combination. |
2.1.2. Determination of design moment and shear
The factored moment and shear can be determined using the simplified method if the requirements are satisfied:
ACI 318-14 (6.5.1)
✓ Members are prismatic.
✓ Loads are uniformly distributed.
✓ L ≤ 3D (0.08 kips/ft per ft ≤ 3 × 0.0825 kips/ft per ft)
✓ There are at least two spans.
✓ The longer of two adjacent spans does not exceed the shorter by more than 20 percent.
Thus, the approximate coefficients can be used. The factored moments and shears are determined and summarized in the following tables.
ACI 318-14 (Table 6.5.2 and Table 6.5.3)
Table 1 - One-Way Slab Design Moment Values | ||
Location | Design Moment Value | |
End Spans | Exterior Support Negative |
|
Mid-span |
| |
Interior Support Negative |
| |
Interior Spans | Mid-span Positive |
|
Support Negative |
| |
Table 2 - One-Way Slab Design Shear Values | |
Location | Design Shear Value |
End Span at Face of First Interior Support |
|
At Face of all other Supports |
|
For the one-way slab of a wide-module joist system, a single layer of longitudinal reinforcement is provided. The first interior support negative moment governs the design as tabulated in Table 1. Therefore, it is favorable to place the single layer reinforcement closer to the top fiber of the concrete slab. The required reinforcement shall be calculated for the first interior support negative moment first. The required reinforcement for the end span positive moment shall also be calculated as the low effective depth due to the reinforcement location may govern the required reinforcement amount. Finally, the required reinforcement for design shall be checked against the minimum shrinkage and temperature reinforcement requirement per ACI 318-14 (24.4.3.2).
Calculate the required reinforcement to resist the first interior support negative moment:
Mu = 0.69 ft-kips/ft
Use welded wire fabric reinforcement, 6 × 6-W5.5 × W5.5 with 1.5 in. concrete cover. The distance from extreme compression fiber to the centroid of longitudinal tension reinforcement, d, is calculated below:
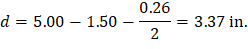
To determine the area of steel, assumptions have to be made whether the section is tension or compression controlled, and regarding the distance between the resultant compression and tension forces along the slab section (jd). In this example, tension-controlled section will be assumed so the reduction factor ϕ is equal to 0.9, and jd will be taken equal to 0.992 × d. The assumptions will be verified once the area of steel is finalized.
Assume
Unit strip width, b = 12 in.
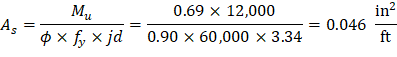
Recalculate ‘a’ for the actual As = 0.046 in.2 per ft:
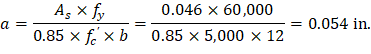
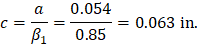
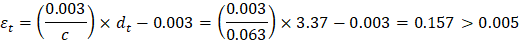
Therefore, the assumption that section is tension-controlled is valid.
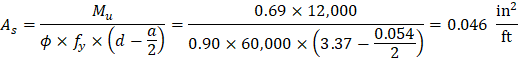
Calculate the required reinforcement to resist the positive moment:
Mu = 0.49 ft-kips/ft
The distance from extreme compression fiber to the centroid of longitudinal tension reinforcement:
d = 5.00 – 3.37 = 1.63 in.
To determine the area of steel, assumptions have to be made whether the section is tension or compression controlled, and regarding the distance between the resultant compression and tension forces along the slab section (jd). In this example, tension-controlled section will be assumed so the reduction factor ϕ is equal to 0.9, and jd will be taken equal to 0.975 × d. The assumptions will be verified once the area of steel is finalized.
Assume
Unit strip width, b = 12 in.
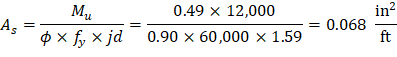
Recalculate ‘a’ for the actual As = 0.068 in.2:
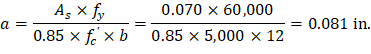
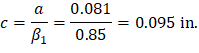
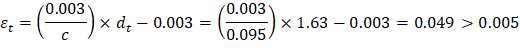
Therefore, the assumption that section is tension-controlled is valid.
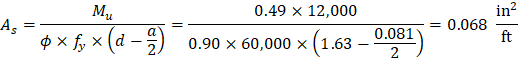
Check the shrinkage and temperature reinforcement requirement:
ACI 318-14 (Table 24.4.3.2)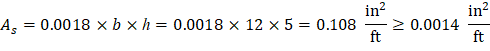
Check reinforcement spacing for crack control:
The maximum spacing of the flexural reinforcement closest to the tension face of the slab shall be:
ACI 318-14 (Table 24.4.3.2) Where: s = Maximum reinforcement spacing for crack control, in. fs = Calculated stress in reinforcement closest to the tension face at service load, ksi cc = The least distance from surface of reinforcement to the tension face, in. Use ACI 318-14 (24.3.2.1) cc = 1.50 in. for reinforcement resisting negative moment at supports (i.e. tension at the top) cc = 3.24 in. for reinforcement resisting positive moment at mid-span (i.e. tension at the bottom)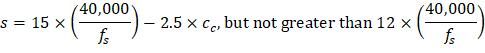
Thus,
At supports
(governs @ support)
But not greater than
At mid-span
(governs @ mid-span)
But not greater than
Therefore, for this one-way slab, the shrinkage and temperature reinforcement requirement per ACI 318-14 (Table 24.4.3.2) governs the required reinforcement area (As = 0.108 in2/ft) and crack control requirement per ACI 318-14 (Table 24.3.2) governs the reinforcement spacing (s = 6.90 in.).
The most feasible reinforcement solution that meets both requirements mentioned above is to provide welded wire fabric reinforcement, 6 × 6 -W5.5 × W5.5. Note that the welded wire reinforcement selected provides minimum shrinkage and temperature reinforcement in the slab direction parallel to the joists as well. Alternately, deformed bars can be utilized in lieu of welded wire fabric. It should be noted that two conditions specific to this design contribute to having such a stringent spacing requirement.
These are listed below:
• The 5 in. slab has a single layer reinforcement that is placed near the top surface (i.e. clear cover from the top surface to the reinforcement is 1.50 in. This result in a high cc value for the calculation of reinforcement spacing for crack control due to positive moment.
• The stress in reinforcement closest to the tension face at service load, fs, is taken as 2/3 fy as permitted by ACI 318-14 without calculation. It is very likely that under the loading considered, the stress in the steel will be lower than 2/3 fy. The fs value is expected to be in the range of 1/3 fy to 1/2 fy. Even if it is assumed to be 1/2 fy, s value will be 12 in.
From Table 2 above, the shear value in end span at face of first interior support governs. The design shear at a distance, d, away from the face of support, Shear strength provided by concrete ACI 318-14 (Eq. 22.5.5.1) Therefore, the slab shear capacity is adequate.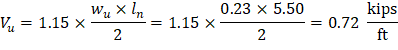
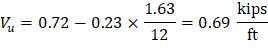
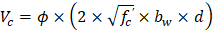
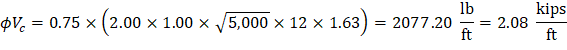
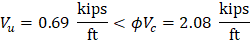
Since the preliminary slab thickness met minimum thickness requirement, the deflection calculations are not required. Unless governed by fire rating requirements; as in this example; lesser thicknesses and consequently cost savings can be achieved through deflection computations. Deflection values are calculated and provided for every model created by spBeam Program and can be used by the engineer to make additional optimization decisions.
2.1.6. Computer Program Solution
spBeam Program can be utilized to analysis and design beams and one-way slab systems. The one-way slab is modeled as 1-ft unit strip supported on ribs. The ribs provide some rotational stiffness at the supports. In spBeam solution, the rotational stiffness is assumed as 32,000* kip-in./rad for modeling the joist supports. Also, for one-way slab run, the rib widths assumed as 6 in. and modeled through dummy columns of 6 in. × 12 in. with zero height (i.e. column stiffness is zero, but the 6 in. dimension of the column is utilized to push the design moments 3 in. from the support centerline). In this example, user-defined bar size #2 is defined in spBeam to represent welded wire fabric, W5.5, with the cross-sectional area of 0.055 in2 (see Figure 4).
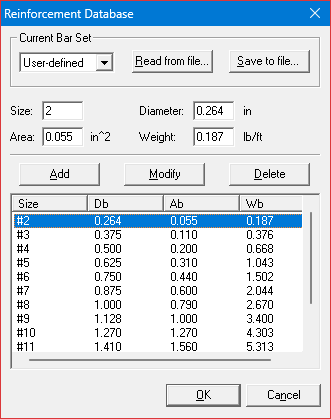
Figure 4 – spBeam Reinforcement Database – User-defined Bar Set
The program calculates the internal forces (shear force and bending moment), moment and shear capacities, immediate and long-term deflections, and required reinforcements. The graphical and text results are provided below for input and output of the spBeam program. The graphical and text results are provided here for both input and output of the spBeam model.

Figure 5 – spBeam Model - Isometric View of 15 Span - 1ft Wide Unit Strip of One-Way Slab
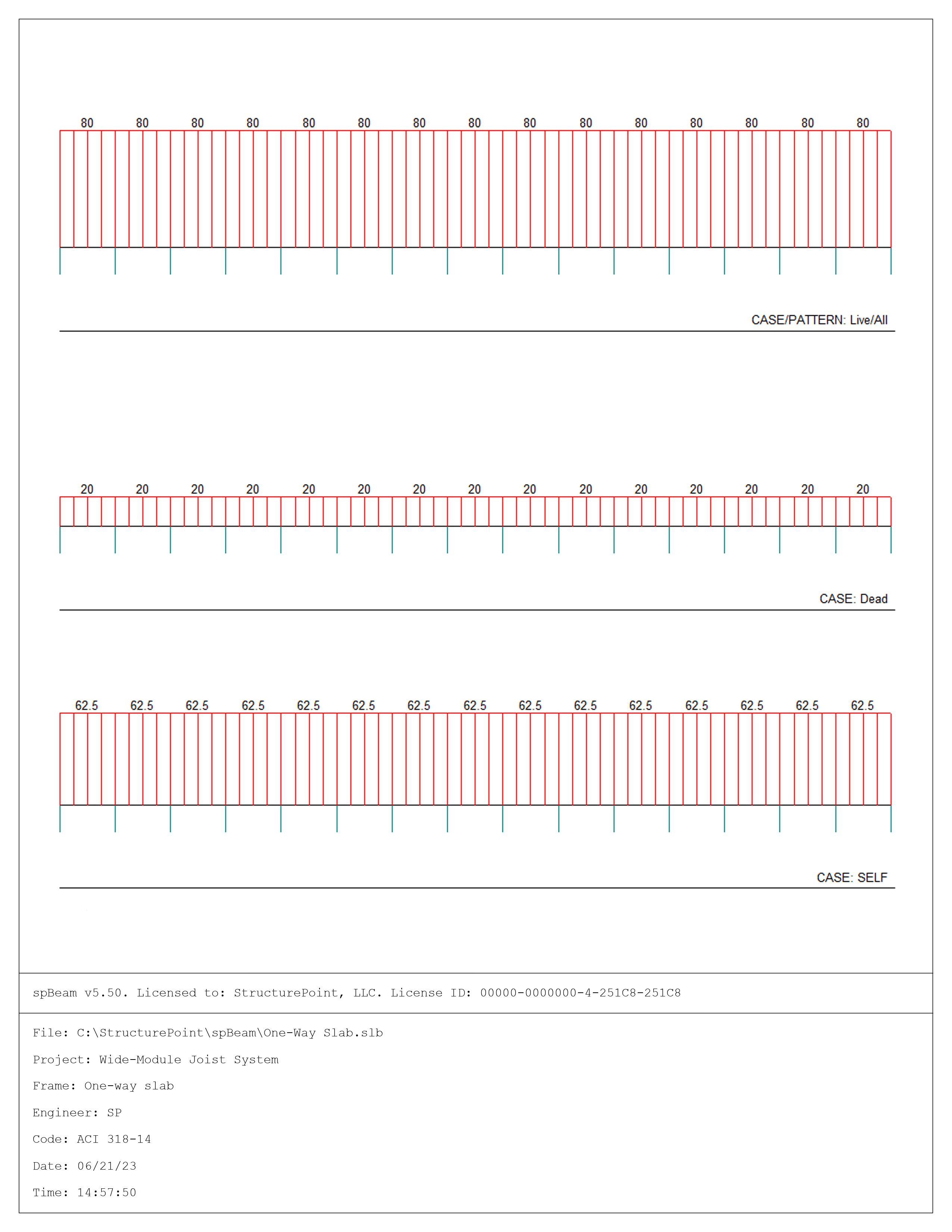
Figure 6 – spBeam Model – Loads (Including Live Load Patterning) units in lb/ft2
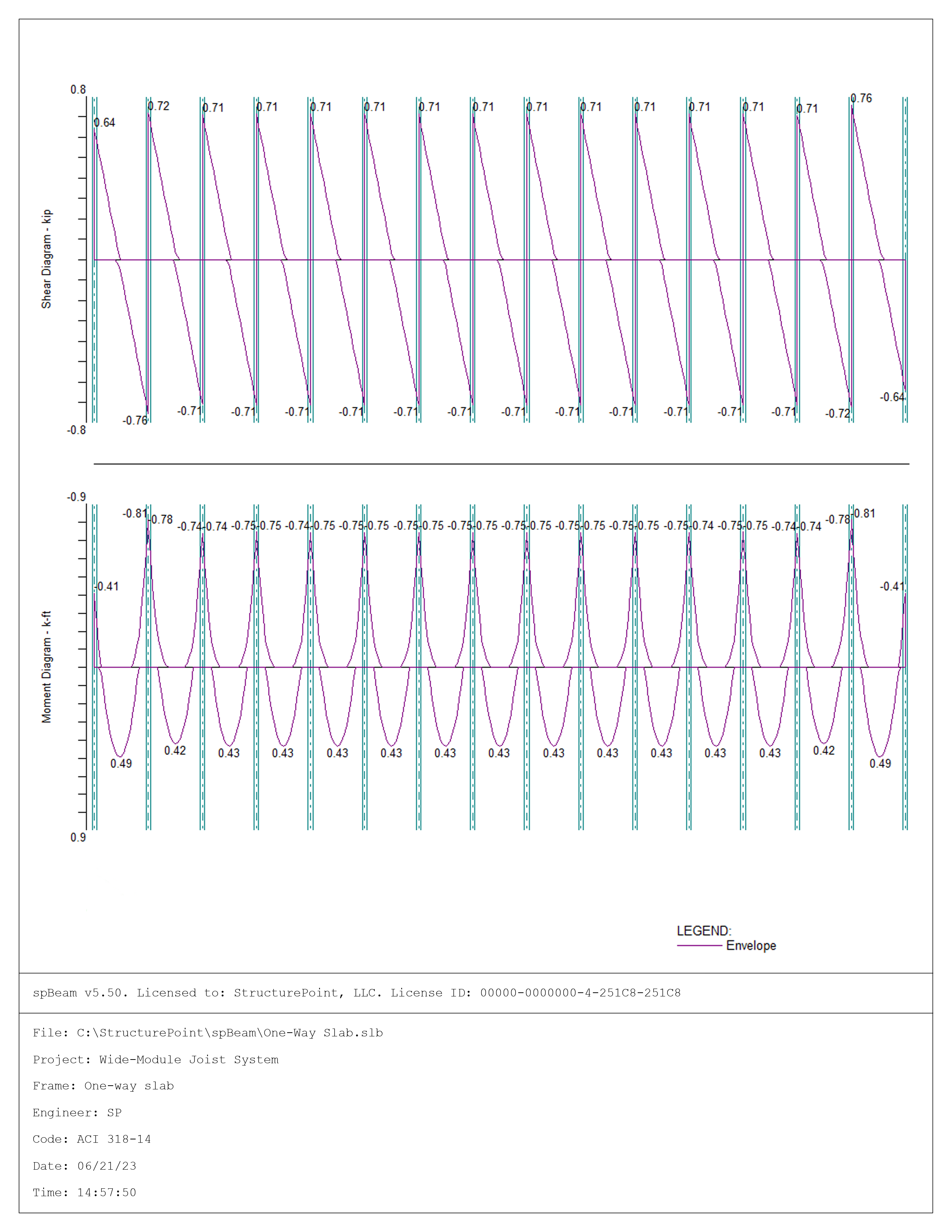
Figure 7 – spBeam Model - Internal Forces (Shear Force Diagram and Bending Moment Diagram)
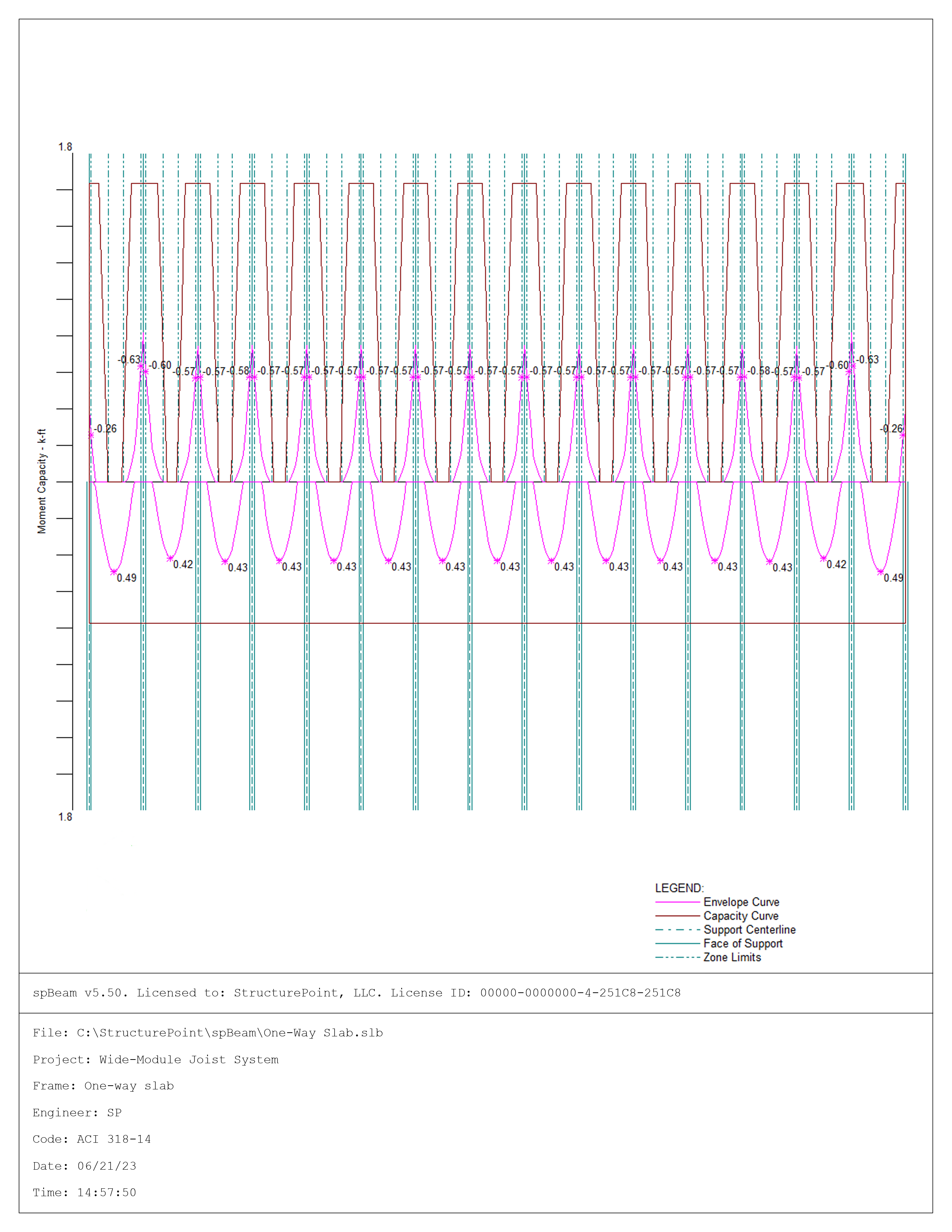
Figure 8 – spBeam Model - Moment Capacity Diagram
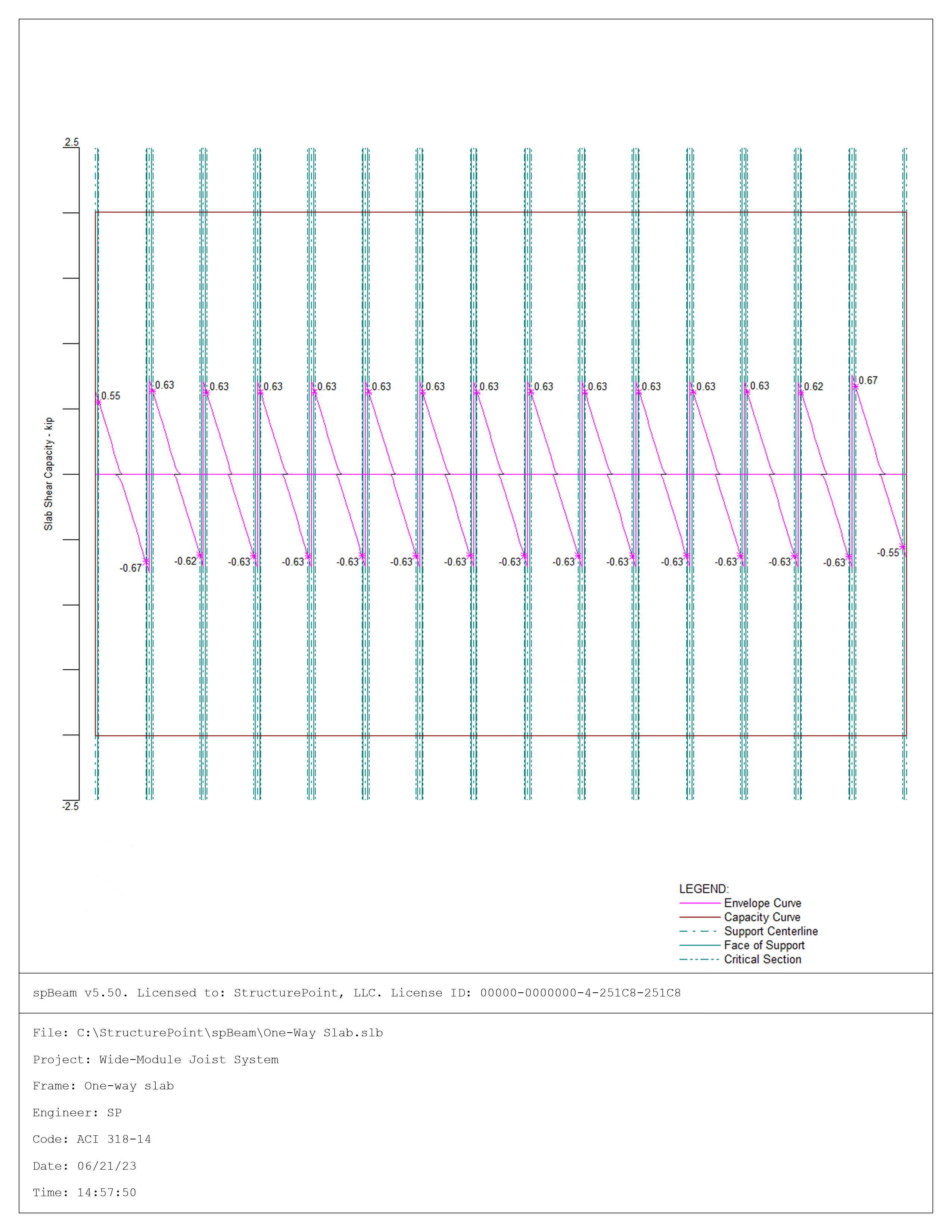
Figure 9 – spBeam Model - Shear Capacity Diagram
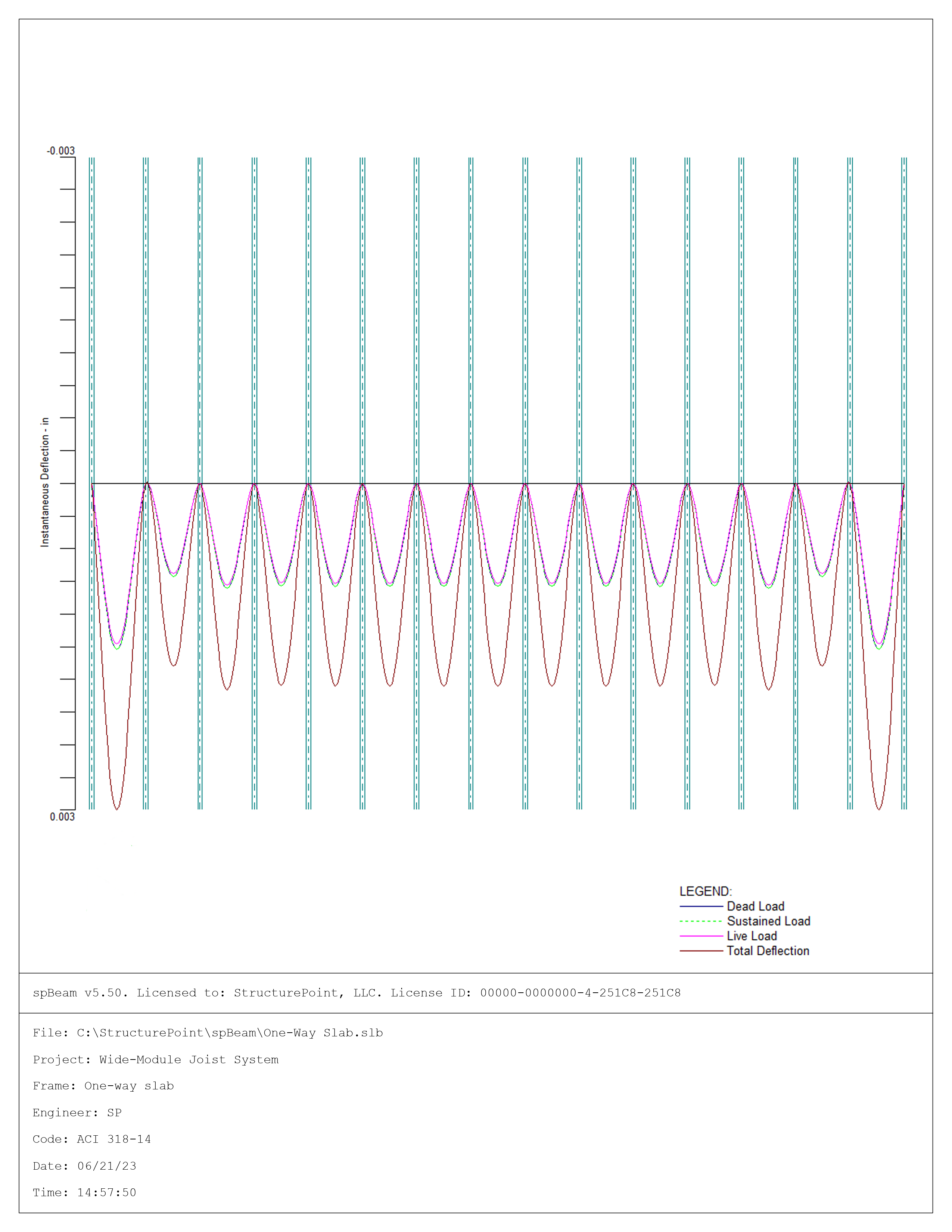
Figure 10 – spBeam Model - Immediate Deflection Diagram

Figure 11 – spBeam Model - Reinforcement Diagram
2.1.7. Summary and Comparison of Results
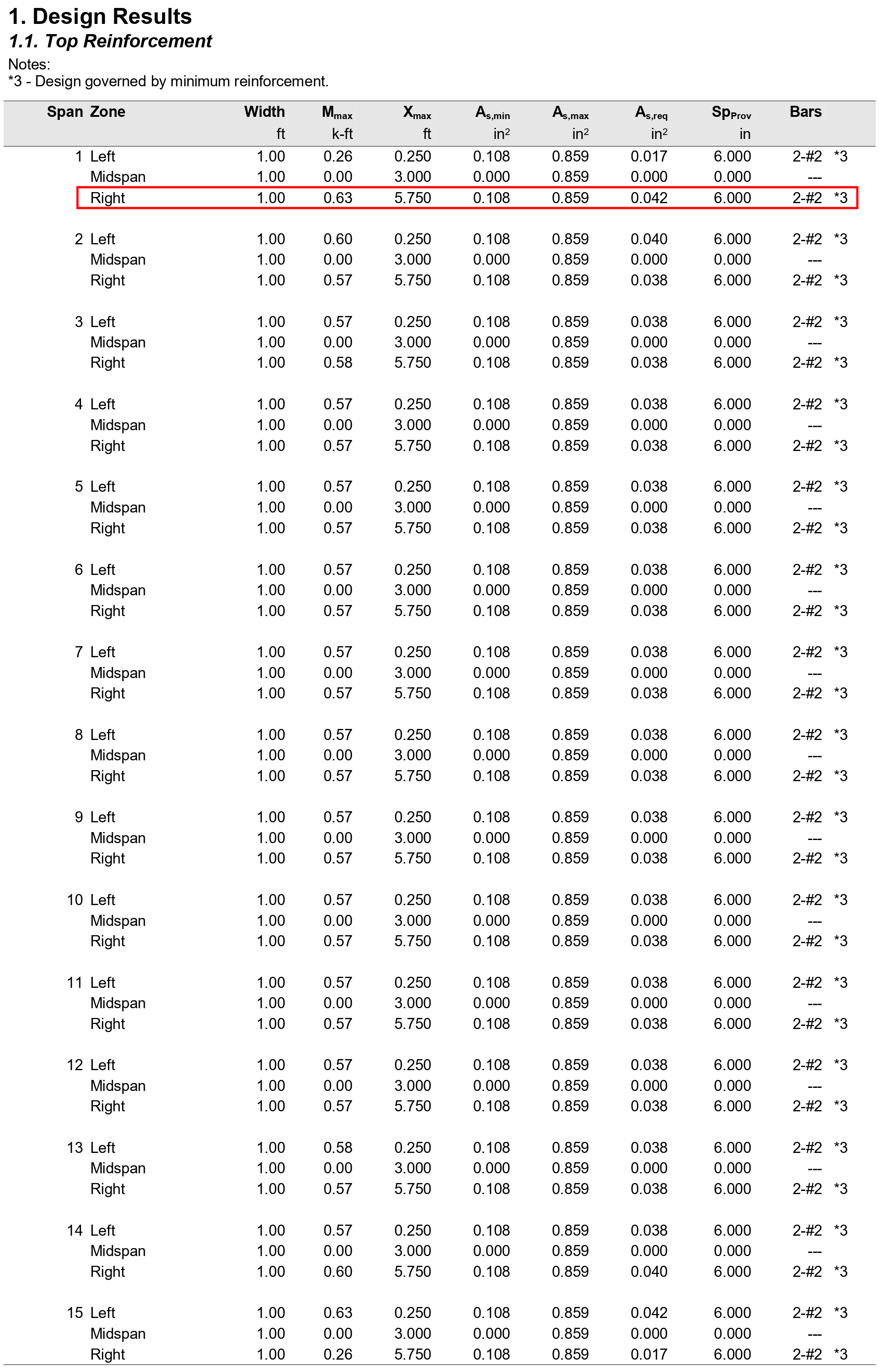
Table 3 - Comparison of Hand Solution with spBeam Solution for One-Way Slab | ||||||
Flexural Design | ||||||
Span Location | Design Moment (ft-kips/ft) | Reinforcement Required for Flexure (in2/ft) | Minimum Reinforcement (in2/ft) (Shrinkage & Temperature Reinforcement) | |||
End Span | Hand | spBeam | Hand | spBeam | Hand | spBeam |
Interior Negative | 0.69 | 0.63 | 0.046 | 0.042 | 0.108 (2-#2) | 0.108 (2-#2) |
Positive | 0.49 | 0.49 | 0.068 | 0.069 | 0.108 (2-#2) | 0.108 (2-#2) |
Shear Design | ||||||
Span Location | Vu (kips/ft) | ϕVn (kips/ft) | ||||
End Span | Hand | spBeam | Hand | spBeam | ||
Interior Negative | 0.69 | 0.67 | 2.08 | 2.08 | ||
2.1.8. Conclusions and Observations
Minimum reinforcement requirement governed flexural design in this example. spBeam program enables the user to enter the rotational support springs as boundary conditions for joist supports and evaluate various analysis and design options beyond the limitations of the simplified method. The coefficients traditionally used to determine moments do not address various types of support and geometry.
Typically, in wide-module joist construction, one-way slab is reinforced with single layer reinforcement placed near the top in the primary direction. As seen in this example, this may cause crack control criteria to govern the reinforcement spacing and consequently, it may warrant the use of welded wire fabric reinforcement instead of deformed bar.
The maximum calculated total immediate (instantaneous) deflection (DL + LL) = 0.003 in., this value can be compared with maximum permissible calculated deflection limitation per project criteria in accordance to ACI 318-14.
ACI 318-14 (Table 24.2.2)
In addition to deflection results, parametric studies can be performed in spBeam to optimize design and detailing results. Note in the reinforcement diagram (Figure 11) 2-#2 for top reinforcement in the span left and right zones as well as span bottom reinforcement. One layer is suitable by inspection (Figure 8) to meet the required area of steel for top and bottom reinforcement.
* Refer to spBeam manual (Chapter 2 – Special Considerations for One and Two-Way Joist Systems)
* Refer to spBeam manual (Chapter 4 – Defining Boundary Conditions, Rotational Stiffness