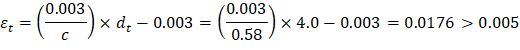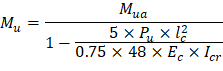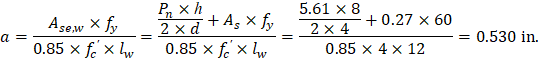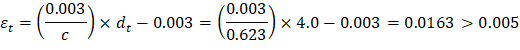Using 14.8 provisions, calculate factored loads as follows for each of the considered load combinations:
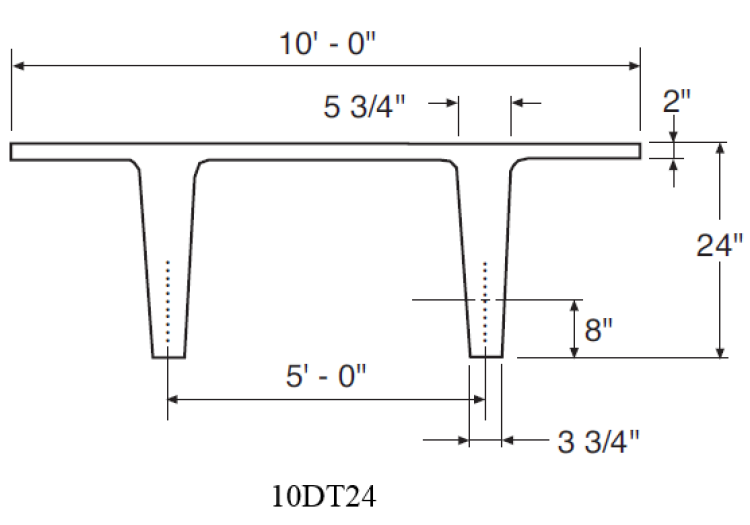
3.1. Roof load per foot width of wall
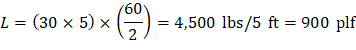
3.2. Calculation of maximum wall forces
The calculation of maximum factored wall forces in accordance with 11.8 is summarized in Figure 2 including moment magnification due to second order (P-Δ) effects.
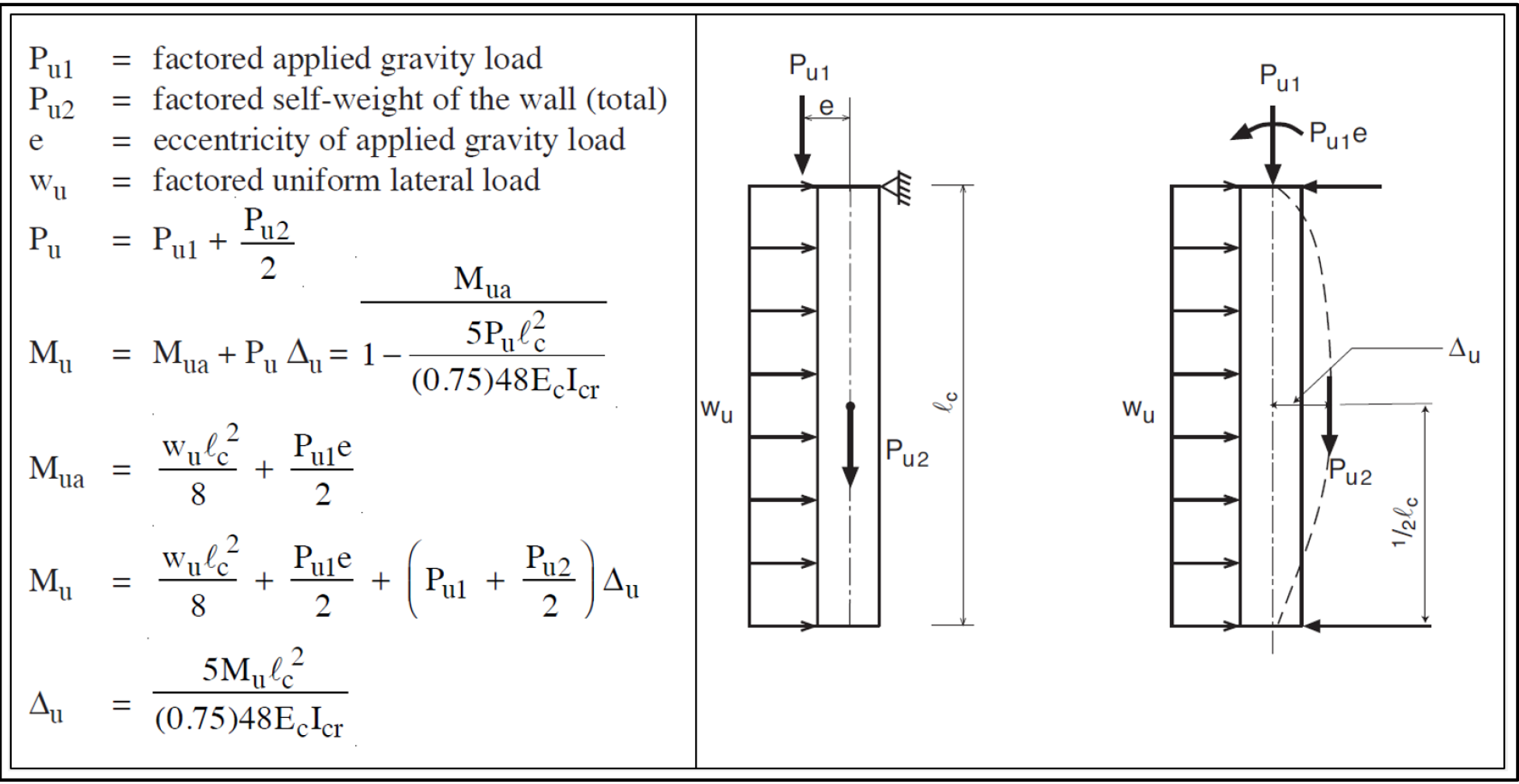
Figure 2 - Wall Structural Analysis According to the Alternative Design of Slender Walls Method (PCA Notes)
For load combination #1 (U = 1.4 D):
ACI 318-14 (11.8.3.1d) Where Mua is the maximum factored moment at midheight of wall due to lateral and eccentric vertical loads, not including PΔ effects. ACI 318-14 (11.8.3.1) ACI 318-14 (19.2.2.1.b) ACI 318-14 (11.8.3.1c) ACI 318-14 (11.8.3.1) Calculate the effective area of longitudinal reinforcement in a slender wall for obtaining an approximate cracked moment of inertia. ACI 318-14 (R11.8.3.1) The following calculation are performed with the effective area of steel in lieu of the actual area of steel.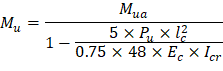
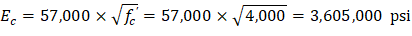
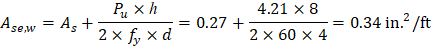
ACI 318-14 (11.8.3.1c) | |
| |
Therefore, section is tension controlled | ACI 318-14 (Table 21.2.2) |
ACI 318-14 (Table 21.2.2) | |
| ACI 318-14 (11.8.3.1d) |
The steps above are repeated for all the considered load combinations, Table 1 shows the factored loads at mid-height of wall for all of these load combinations.
Table 1 - Factored load combinations at mid-height of wall | |||||||||||
Load Combination | Pu, kips | Mua, in.-kips | Ec, ksi | n | Ase,w, in.2/ft | a, in. | c, in. | Icr, in.4 | εt, in./in. | ϕ | Mu, in.-kips |
1.4 D | 4.21 | 3.74 | 3,605 | 8 | 0.34 | 0.50 | 0.58 | 32.4 | 0.0176 | 0.9 | 5.25 |
1.2 D + 1.6 Lr + 0.8 W | 5.04 | 19.53 | 3,605 | 8 | 0.35 | 0.52 | 0.61 | 33.4 | 0.0168 | 0.9 | 29.38 |
1.2 D + 0.5 Lr + 1.6 W | 4.05 | 32.61 | 3,605 | 8 | 0.33 | 0.49 | 0.58 | 32.3 | 0.0178 | 0.9 | 45.22 |
0.9 D + 1.6 W | 2.70 | 31.21 | 3,605 | 8 | 0.31 | 0.46 | 0.54 | 30.7 | 0.0193 | 0.9 | 38.80 |
3.3. Tension-controlled verification
ACI 318-14 (11.8.1.1(b)) | |
For this check use the largest Pu (5.04 kips) from load combination 2 to envelop all the considered combinations. | |
| |
| |
Therefore, section is tension controlled | ACI 318-14 (Table 21.2.2) |