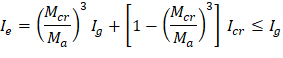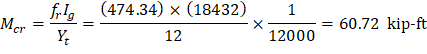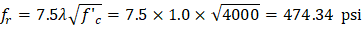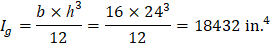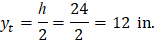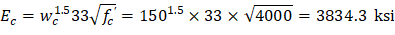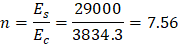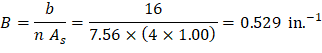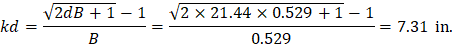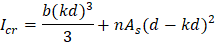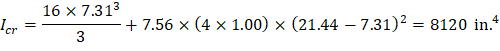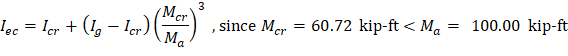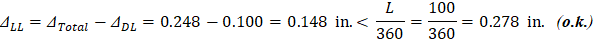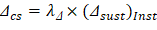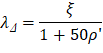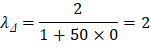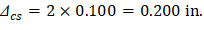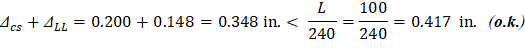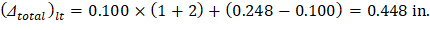6. Deflection Control (Serviceability Requirements)
Since the preliminary beam depth met minimum depth requirement, the deflection calculations are not required. However, the calculations of immediate and time-dependent deflections are covered in detail in this section for illustration and comparison with spBeam model results for cantilever beam.
6.1. Immediate (Instantaneous) Deflections
Elastic analysis for three service load levels (D, D + Lsustained, D + LFull) is used to obtain immediate deflections of the cantilever beam in this example. However, other procedures may be used if they result in predictions of deflection in reasonable agreement with the results of comprehensive tests.
The effective moment of inertia procedure described in the Code is considered sufficiently accurate to estimate deflections. The effective moment of inertia, Ie, was developed to provide a transition between the upper and lower bounds of Ig and Icr as a function of the ratio Mcr/Ma.
Unless deflections are determined by a more comprehensive analysis, immediate deflection shall be computed using elastic deflection equations using Ie from Eq. (24.2.3.5a) at midspan for simple and continuous spans, and at the support for cantilevers.
ACI 318-14 (24.2.3.7)
The effective moment of inertia (Ie) is used to account for the cracking effect on the flexural stiffness of the beam. Ie for uncracked section (Mcr > Ma) is equal to Ig. When the section is cracked (Mcr < Ma), then the following equation should be used:
| ACI 318-14 (Eq. 24.2.3.5a) |
Where:
Ma = Maximum moment in member due to service loads at stage deflection is calculated.
The values of the maximum moments for the three service load levels are calculated from structural analysis as shown previously (sustained live load = 0).
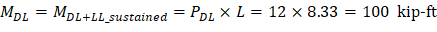
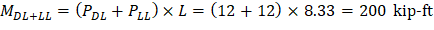
Mcr = cracking moment.
| ACI 318-14 (Eq. 24.2.3.5b) |
fr = Modulus of rapture of concrete | |
| ACI 318-14 (Eq. 19.2.3.1) |
Ig = Moment of inertia of the gross uncracked concrete section | |
| |
| |
Icr = moment of inertia of the cracked section transformed to concrete. | CAC Concrete Design Handbook 4th Edition (5.2.3) |
The critical section at midspan is reinforced with 4 – #9 bars.
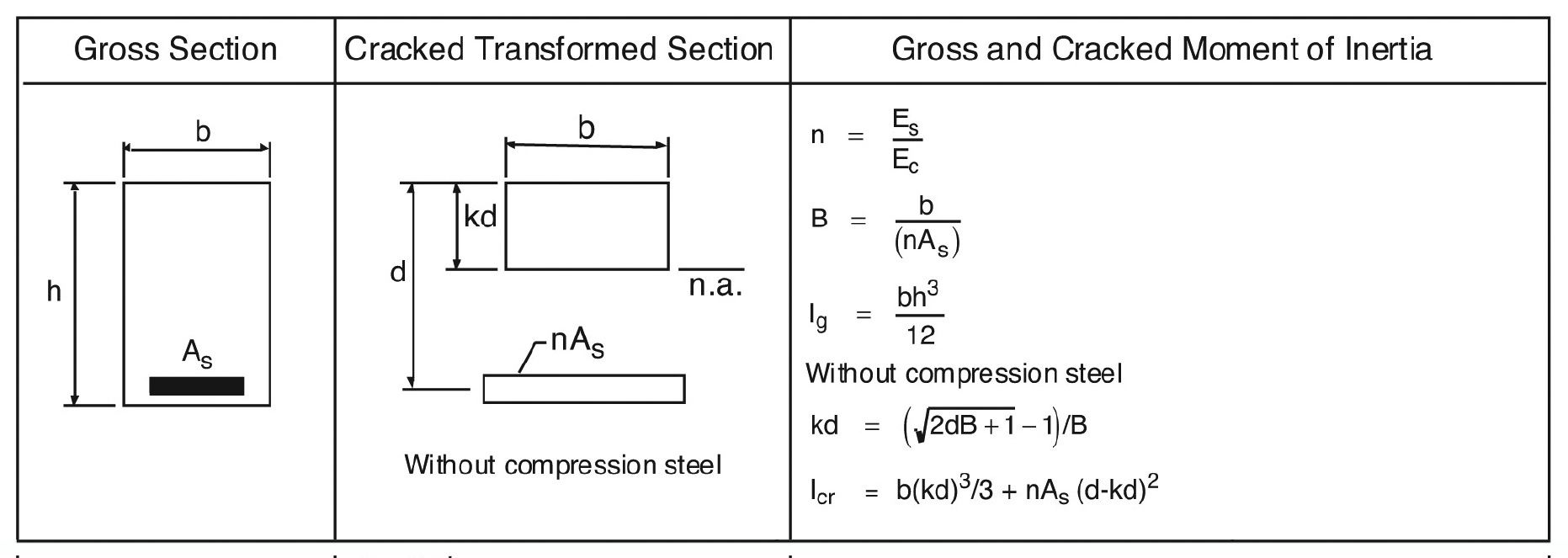
Figure 6 – Gross and Cracked Moment of Inertia of Rectangular Section (PCA Notes Table 10-2)
Ec = Modulus of elasticity of concrete. | |
| ACI 318-14 (19.2.2.1.a) |
| PCA Notes on ACI 318-11 (Table 10-2) |
| PCA Notes on ACI 318-11 (Table 10-2) |
| PCA Notes on ACI 318-11 (Table 10-2) |
| PCA Notes on ACI 318-11 (Table 10-2) |
|
For dead load service load level:
| ACI 318-14 (24.2.3.5a) |
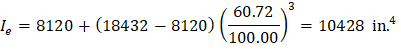
The following Table provides a summary of the required parameters and calculated values needed for deflection calculation.
Table 1 – Effective Moment of Inertia Calculations (at midspan) | ||||||||
Ig, | Icr, | Ma, kip-ft | Mcr, | Ie, in.4 | ||||
D | D + LLSus | D + Lfull | D | D + LLSus | D + Lfull | |||
18432 | 8120 | 100.00 | 100.00 | 200.00 | 62.72 | 10428 | 10428 | 8409 |
After obtaining the effective moment of inertia, the maximum span deflection for the cantilever beam (at the free end) can be obtained from any available procedures or design aids (see Figure 3).
(at the free end)
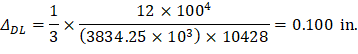
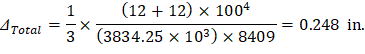
| ACI 318-14 (Table 24.2.2) |
6.2. Time-Dependent (Long-Term) Deflections (Δlt)
The additional time-dependent (long-term) deflection resulting from creep and shrinkage (Δcs) are estimated as follows.
| PCA Notes on ACI 318-11 (9.5.2.5 Eq. 4) |
The total time-dependent (long-term) deflection is calculated as: | |
CSA A23.3-04 (N9.8.2.5) | |
Where: | |
(Δsust)Inst = Immediate (instantaneous) deflection due to sustained load, in. | |
| ACI 318-14 (24.2.4.1.1) |
(Δtotal)lt = Time-dependent (long-term) total deflection, in. | |
(Δtotal)lnst = Total immediate (instantaneous) deflection, in. | |
For the exterior span | |
ξ = 2, consider the sustained load duration to be 60 months or more. | ACI 318-14 (Table 24.2.4.1.3) |
ρ` = 0, conservatively. | |
| |
| |
| ACI 318-14 (Table 24.2.2) |
|