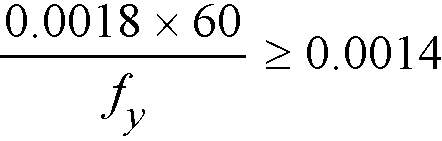2

METHOD OF SOLUTION

 

2.1Introduction

The user should be aware of the assumptions made by the program during the design stage. These include details regarding loading, strip widths, reinforcement selection, deflection computations, material quantities, etc.

2.2Geometric Checks

spSlab and spBeam provide various geometric checks to avoid an analysis with an inconsistent system. Dimensions of slabs, beams, drops, bands and column capitals are checked and modified to produce a code compliant system.

If a slab cantilever length is less than one-half the column dimension in the direction of analysis, c₁, or less than the lateral extension of the transverse beam into the cantilever, the cantilever length will be increased to the larger of these two lengths. If the slab width is less than one-half the column dimension transverse to the direction of analysis, c₂, or less than one-half the longitudinal beam width, the slab width will be increased to the larger of these two widths.

If a drop panel extends beyond the end of a slab cantilever, the drop panel dimensions will be reduced so that it extends only to the cantilever tip.

Guidance is absent from all standards and reference documents regarding continuous extension of drop panels between supports. If a slab band is discontinuous, to model this condition, it must be completed with a user-defined drop panel of corresponding width and thickness on a discontinuous end, as a minimum, in order to complete the analysis.

When a column capital is defined, the program checks if capital side slope (depth/extension ratio) is more than 1, i.e. the angle between capital side and column axis is no greater than 45 degrees¹. The upper limit for the side slope is 50. If a column with capital frames into a drop panel (or a beam), extension of the capital will be automatically adjusted – if necessary – so that projected sides of the capital do not fall outside of the drop panel (or the beam) edges before reaching slab soffit (see Figure 2-1). The modified column capital extension will be used when computing column stiffness and in punching shear calculations.

 

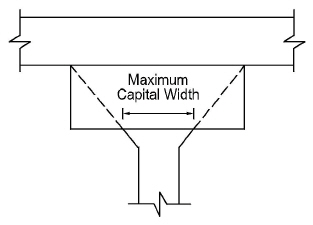
Figure 2.1 Maximum Capital Width

2.3Code Checks

2.3.1Minimum Thickness - One-Way Construction

The program checks beam or one-way slab thickness based on minimum requirement for ACI-318² code as specified in Table 9.5(a) or for CSA code³ according to Table 9.2. For lightweight concrete with density

90 lb/ft³ ≤ w_c ≤ 115 lb/ft³ [1440 kg/m³ ≤ w_c ≤ 1840 kg/m³] for ACI 318-14, ACI 318-11, and ACI 318-08

90 lb/ft³ ≤ w_c ≤ 120 lb/ft³ [1440 kg/m³ ≤ w_c ≤ 1920 kg/m³] for ACI 318-05

90 lb/ft³ ≤ w_c ≤ 120 lb/ft³ [1500 kg/m³ ≤ w_c ≤ 2000 kg/m³] for ACI 318-02, and ACI 318-99,

the minimum slab thickness is additionally increased by adjustment factor (1.65 – 0.005w_c), but not less than 1.09. For CSA standards, the adjustment is calculated as (1.65 – 0.0003w_c), but not less than 1.0, for structural low density (w_c ≤ 1850 kg/m³) and structural semi-low density (1850 kg/m³ ≤ w_c ≤ 2150 kg/m³) concrete⁴.

2.3.2Minimum Slab Thickness - Two-Way Construction

The program checks slab thickness against minimum slab thickness defined by design standards for two-way systems with long to short span ratio not greater than 2.0⁵. Slabs with thickness below the minimum value will be flagged by the program, however, they are allowed provided that calculated deflections do not exceed maximum permissible computed deflections⁶.

For two-way system with a long to short span ratio greater than 2.0, the program will calculate minimum thickness requirements based on the provisions of one-way construction including any cantilevered spans.

Minimum thickness of slabs with beams spanning between supports on all sides is calculated for ACI 318 codes in US customary units from⁷

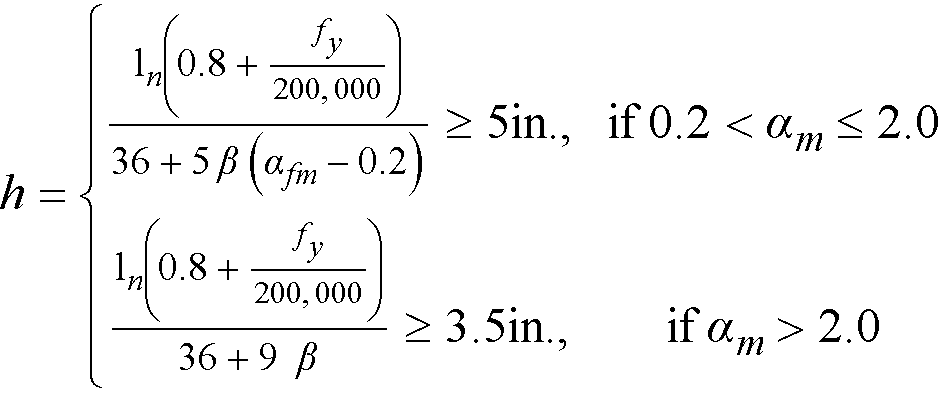      Eq. 2-1

in metric unit system for ACI 318-14, ACI 318-11, ACI 318-08, and ACI 318-05 from⁸

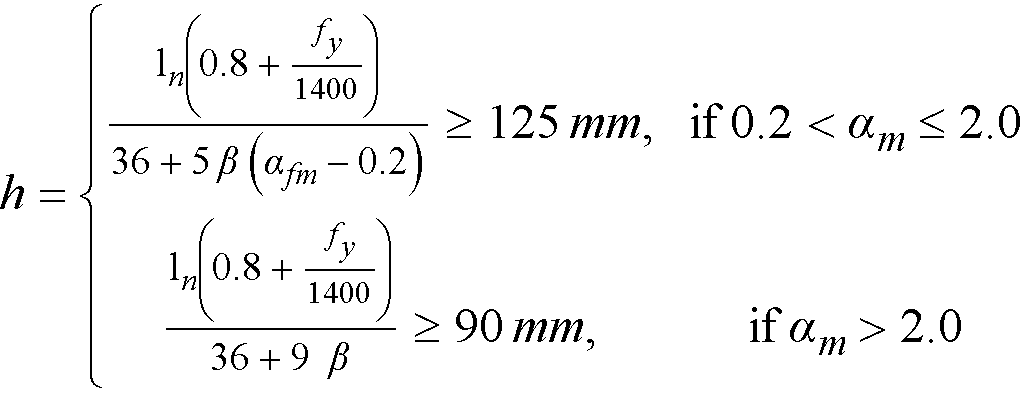      Eq. 2-2

and in metric unit system for ACI 318-02 and ACI 318-99 from⁹

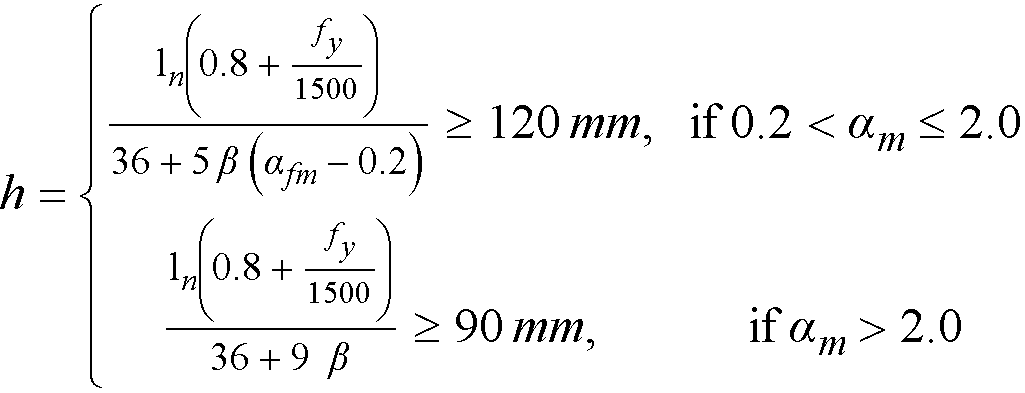      Eq. 2-3

where

l_n   =   longer clear span measured face-to-face of beams,

β   =   ratio of the clear spans in long to short direction,

f_y   =   yield stress of reinforcing steel,

α_m   =   average value of α, the ratio of flexural stiffness of a beam section to the flexural stiffness of a width of slab bounded laterally by centerlines of adjacent panels on either side of the beam, for all beams supporting the edges of a slab panel.

The program assumes that beams are present on all sides of a panel if the span under consideration includes a longitudinal beam and there are transverse beams defined at both ends of the span. If this assumption is satisfied but in reality beams are not present on all sides (e.g. design strip next to the one under consideration has no longitudinal beam) then the user is advised to check deflections even if slab thickness is larger than the minimum slab thickness reported by the program.

For the design of ACI slabs without beams (α_m ≤ 0.2) spanning between interior supports the minimum thickness shall conform to ACI 318 Table 9.5(c) and will not be less than 5.0 in. [125 mm for ACI 318M-11/08/05 or 120 mm for ACI 318M-02/99] for flat plates (slabs without drop panel) and not less than 4.0 in. [100 mm] for two-way flat slab systems (slab with drop panels)¹⁰. For flat slabs that contain valid drop panels (see Figure 2-2), Table 9.5(c) reduces the minimum thickness by approximately 10%. For values of f_y between the ones given in the table, minimum thickness is determined by linear interpolation.

For design strips that have neither beams between all supports nor beams between interior supports (e.g. exterior strips with beams on the outside edges only), the program reports maximum value of minimum slab thickness resulting from both Table 9-5(c) and Equations. However, since this case is not explicitly covered by the ACI code, the user is advised to check deflections even if slab thickness is larger than the minimum slab thickness reported by the program.

For CSA A23.3 standard¹¹, the minimum thickness of slab with beams spanning between all supports is

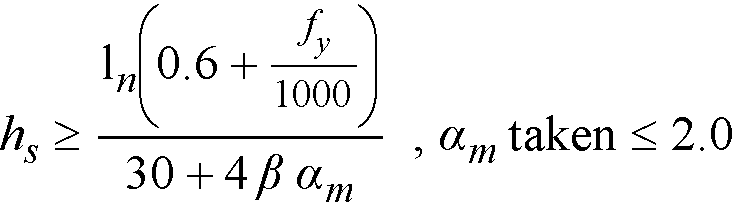      Eq. 2-4

with the value of α_m evaluated for CSA A23.3-04 using the following beam moment of inertia

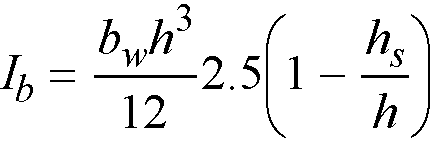      Eq. 2-5

For flat plates and slabs with column capitals¹², the minimum slab thickness is

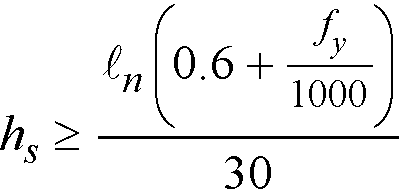      Eq. 2-6

For slabs with drop panels¹³, the minimum slab thickness satisfies the conditions

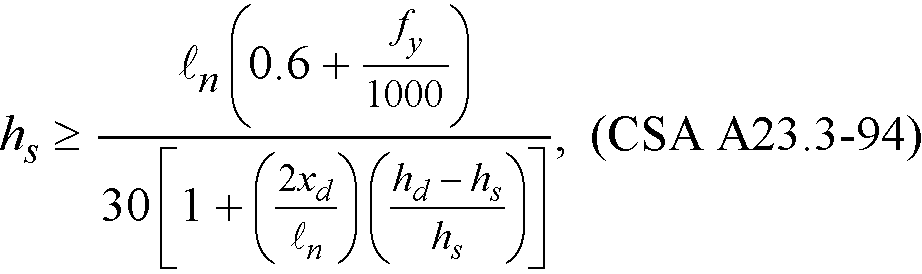      Eq. 2-7

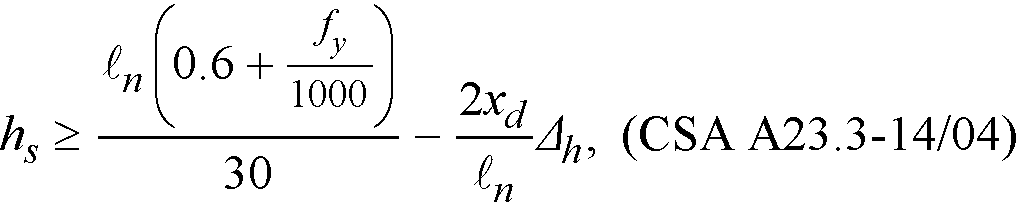      Eq. 2-8

where (h_d − h_s) shall not be greater than h_s and

x_d   =   dimension from face of column to edge of drop panel, but not more than ℓ_n/4

2x_d/ℓ_n   =   the smaller of the values determined in the two directions

D_h    =   additional thickness of the drop panel below the soffit of the slab and shall not be taken more than h_s.

The minimum thickness in a span that contains a discontinuous edge will be increased by 10%, if the edge beam provided has a stiffness ratio, α, of less than 0.80¹⁴. The first and last spans are considered to contain a discontinuous edge as well as a span that contains an exterior edge.

The minimum thickness of slab bands follows the requirements for the beams¹⁵.

2.3.3Drop Panel Dimensions

Per ACI¹⁶, a valid drop must extend in each direction at least one-sixth the center-to-center span length in that direction (Figure 2-2). The depth of an invalid drop will not be used in the calculation of the depth used to reduce the amount of negative reinforcement required over a column¹⁷. If the valid drop depth is greater than one-quarter the distance from the edge of the drop panel to the face of the column (x) the excess depth exceeding ¼x will not be considered in the calculation of the effective depth used to reduce the amount of negative reinforcement required at a column (Figure 2-3)¹⁸. Slabs that contain valid drops are allowed a 10% decrease in minimum slab depth¹⁹.

 

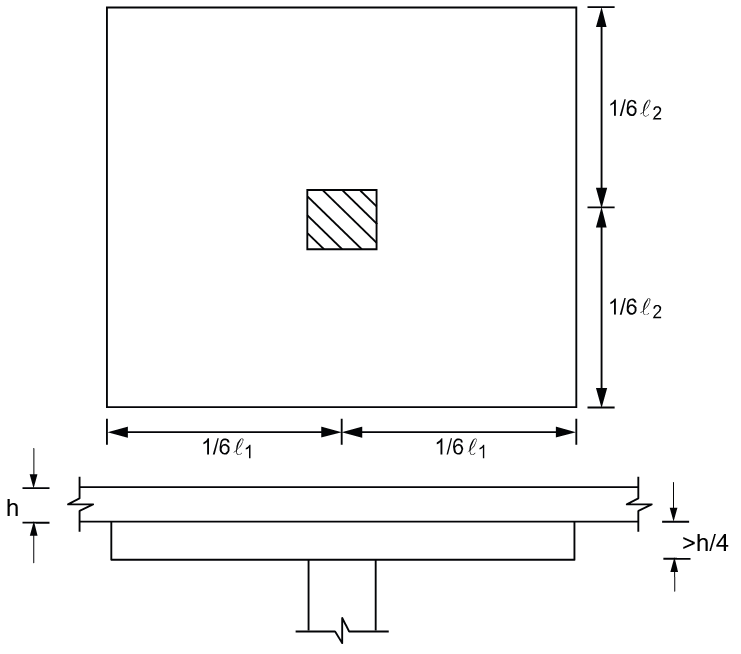
Figure 2.2 Valid Drop Dimensions

The input drop dimensions will be used for self-weight computations, when computing slab stiffness to determine deflections, moments, shears, and when computing punching shear around a column²⁰.

 

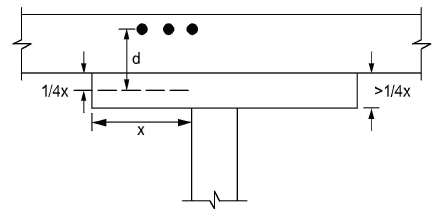
Figure 2.3 Excess Drop Depth

2.3.4Beam Dimensions

The program follows linear distribution of strain (plain section) assumption²¹ for flexure design which is applicable to shallow flexural members. In case of deep beams²², design standards recommend using non-linear distribution of strain or strut-and-tie method. The program checks beam dimensions and if a beam with the following clear span, l_n, to overall depth, h, ratio is found

      Eq. 2-9

a warning is issued alerting the user that additional deep beam design and detailing is required. For cantilevers, the warning is issued only if their clear span is larger than overall depth.

2.4Special Considerations for One and Two-Way Joist Systems

2.4.1Rib Dimensions

Rib dimensions will be considered valid if the rib width is at least 4 in. [100 mm], the depth is no more than 3-1/2 times the rib width, and the clear spacing between ribs does not exceed 30 in. [800 mm]²³. If rib dimensions do not meet these requirements (e.g. wide module joist systems) the code requires such ribs to be designed as beams²⁴. The program treats the design of wide-spaced joists the same way as for valid slabs, regardless of code limitation. If the code limits are exceeded, the condition is flagged and the 10% increase of rib shear capacity is not used. The user is then responsible to validate the resulting design and reconcile the code requirements.

2.4.2Minimum Thickness for Joist Systems

The minimum slab thickness allowed for joist slabs is one-twelfth the clear rib spacing, or 1.5 in [40 mm] for ACI code²⁵ and 50mm for CSA code²⁶.

2.4.3Joist System Analysis and Design

For the purposes of analysis and design, the program replaces the ribbed slab with solid slabs of equivalent moment of inertia, weight, punching shear capacity, and one-way shear capacity.

The equivalent thickness based on system weight is used to compute the system self-weight. This thickness, h_w, is given by

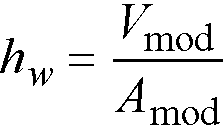      Eq. 2-10

where

V_mod   =   the volume of one joist module,

A_mod   =   the plan area of one joist module.

 

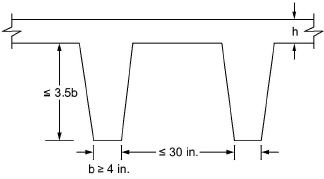
Figure 2.4 Valid Rib Dimensions

The equivalent thickness based on moment of inertia is used to compute slab stiffness. The ribs spanning in the transverse direction are not considered in the stiffness computations. This thickness, h_MI, is given by

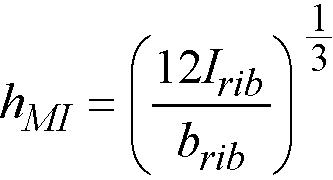      Eq. 2-11

where

I_rib   =   moment of inertia of one joist section between centerlines of ribs.

b_rib   =   the center-to-center distance of two ribs (clear rib spacing plus rib width).

The drop panel depth for two-way joist (waffle) slab systems is set equal to the rib depth. The equivalent drop depth based on moment of inertia, d_MI, is given by

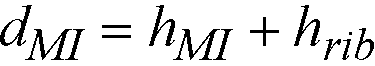      Eq. 2-12

where

h_rib   =   rib depth below slab,

h_MI   =   equivalent slab thickness based on moment of inertia.

A drop depth entered for a waffle slab system other than 0 will be added to d_MI, thus extending below the ribs.

One–way shear capacity, V_c (increased by 10% for ACI code²⁷), is calculated assuming the shear cross-section area consisting of ribs and the portion of slab above, decreased by concrete cover. For such section the equivalent shear width of single rib is calculated from the formula

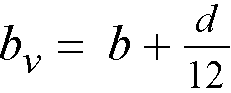      Eq. 2-13

where

b   =   rib width,

d   =   distance from extreme compression fiber to tension reinforcement centroid.

The equivalent thickness based on shear area is used to compute the area of concrete section resisting punching shear transfer, A_c around drop panels in two-way joist (waffle) systems. The equivalent slab thickness, h_V, used to compute A_c, is given by

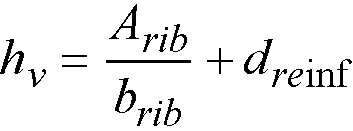      Eq. 2-14

where

A_rib   =   the entire rib area below the slab plus the slab thickness minus the distance to the reinforcement centroid, d_reinf, within the rib width, i.e., the slab depth between the ribs is not considered as contributing to shear capacity,

b_rib   =   the center-to-center distance of two ribs (clear rib spacing plus rib width),

d_reinf   =   the distance to reinforcement centroid from the slab top at the support

When calculating flexural capacity for negative bending moments, the distance between center of top reinforcement to the soffit of the rib is used as an effective depth, d, while assuming the width of compression zone as equal to the center-to-center distance of two ribs (b_rib). This assumption results in higher estimates of negative moment capacity since the space between ribs is void. The user may switch to a single rib design or investigation as a beam in order to consider rib width only in the compression zone.

2.5Material Properties

By entering the concrete density and compressive strength of the members, default values for the other concrete properties are determined. The slabs/beams and columns may have different concrete properties.

The density of concrete is used to determine the type of concrete, modulus of elasticity, and self-weight.

The concrete type is determined in accordance with Table 2-1.

Table 2.1 Concrete Weight Classification

Once the compressive strength of concrete 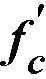 is input, various parameters are set to their default values.

The modulus of elasticity is computed as²⁸

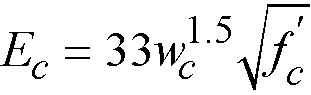      Eq. 2-15

where

w_c   =   the unit weight of concrete.

For CSA A23.3 standard²⁹

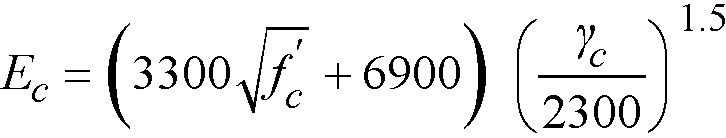      Eq. 2-16

where

γ_c   =   the density of concrete.

The square root of 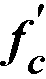is limited to 100 psi for the computation of shear strength provided by concrete, V_c, and development lengths.³⁰

For CSA A23.3-14/04 standard the value of square root of 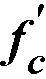 used to calculate factored shear resistance v_r shall not exceed 8MPa.³¹

The modulus of rupture is used to determine the cracking moment when computing the effective moment of inertia in deflection calculations. For ACI 318 code, the default value of modulus of rupture, f_r, is set equal to³²

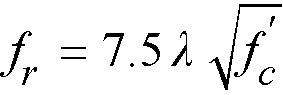      Eq. 2-17

and for the CSA A23.3 standard, the default value of modulus of rupture f_r is³³

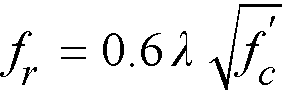      Eq. 2-18

For two-way slabs analyzed in accordance with CSA A23.3-94 as well as for beams, one-way, and two-way slabs analyzed in accordance with CSA A23.3-14/04, the default value is reduced to its half value³⁴, i.e.

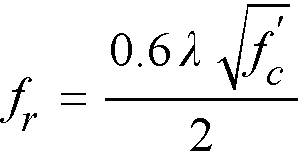      Eq. 2-19

Factor λ reflecting the reduced mechanical properties of lightweight concrete is equal to³⁵ 1.00 for normal density concrete, 0.85 for sand-lightweight (structural semi-low-density) concrete, and 0.75 for all-lightweight (structural low-density) concrete. Refer to Table 2-1 for determination of concrete type.

There is no limit imposed on f_r. Entering a large value of f_r will produce deflections based on gross properties (i.e. uncracked sections).

The default values for the longitudinal reinforcement yield strength, f_y, and shear reinforcement yield strength, f_yv, if applicable, are set equal to 60 ksi [413 MPa] for ACI and 400 MPa for CSA.

2.6Equivalent Frame Method

The equivalent frame method, as described in the code³⁶, is used by spSlab for both analysis and design. The code specifies procedures for the analysis and design of slab systems reinforced for flexure in more than one direction, with or without beams between the supports. A two-way slab³⁷ system, including the slab and its supporting beams, columns, and walls may be designed by either of the following procedures

•The Direct Design Method

•The Equivalent Frame Method

spSlab uses the Equivalent Frame Method of analysis which is based on extensive analytical and experimental studies conducted at the University of Illinois. Note also that there are no restrictions on the number of slab spans or on dead-to-live load ratios in this method of analysis.

The first step in the frame analysis is to divide the three-dimensional building into a series of two-dimensional frames extending to the full height of the building. Horizontal members for each frame are formed by slab strips as shown in Fig. 2-5. For vertical loads, each story (floor and/or roof) may be analyzed separately with the supporting columns being considered fixed at their remote ends (Figure 2-6).

The required reinforcing and resulting deflections for an interior or exterior panel in a floor system shall be combined from the analysis of two equivalent frames in orthogonal directions in order to arrive at the final design.

2.6.1Stiffness Characteristics

The stiffness factors for the horizontal members (the slab beams) and the vertical members (the equivalent columns) are determined using segmental approach.

 

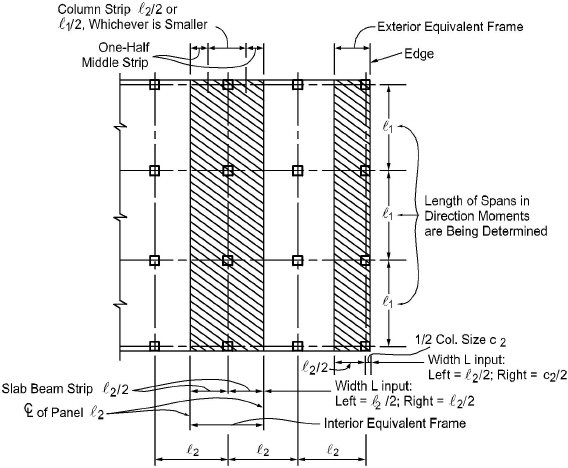
Figure 2.5 Design strips

2.6.2Slab Beams

The moment of inertia of the slab beam elements between the faces of the columns (or column capitals) is based on the uncracked section of the concrete including beams or drop panels. The moment of inertia from the face of the column (or capital) to the centerline of the column (or capital) is considered finite and is dependent on the transverse dimensions of the panel and support. This reduced stiffness (as compared to the infinite stiffness assumed in previous codes) is intended to soften the slab at the joint to account for the flexibility of the slab away from the support. This is consistent with provisions of the code.³⁸ Figure 2-7 shows the changes in stiffness between a slab, and a drop panel, and a column (or capital).

 

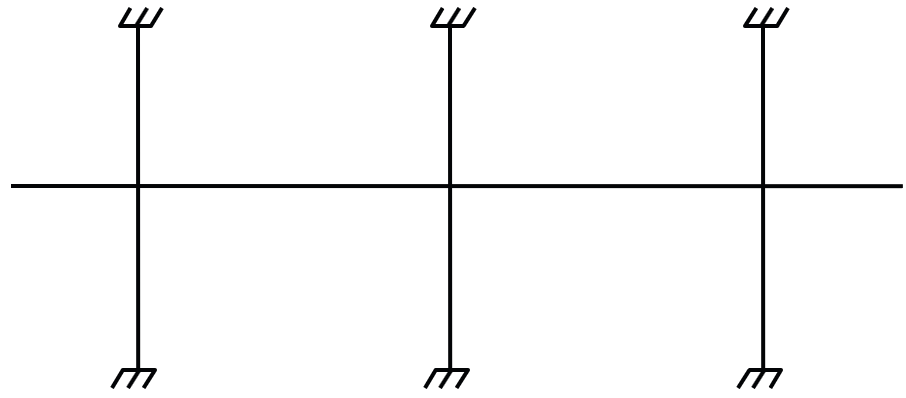
Figure 2.6 Analytical model for vertical loads for a typical story

2.6.3Columns

The computation of the column stiffness is more complicated as it utilizes the concept of an equivalent column. Theoretical slab studies have shown that the positive moment in a slab may increase under pattern loads, even if rigid columns are used, because of the flexibility of the slab away from the column. However, if a two-dimensional frame analysis is applied to a structure with rigid columns, pattern loads will have little effect.

 

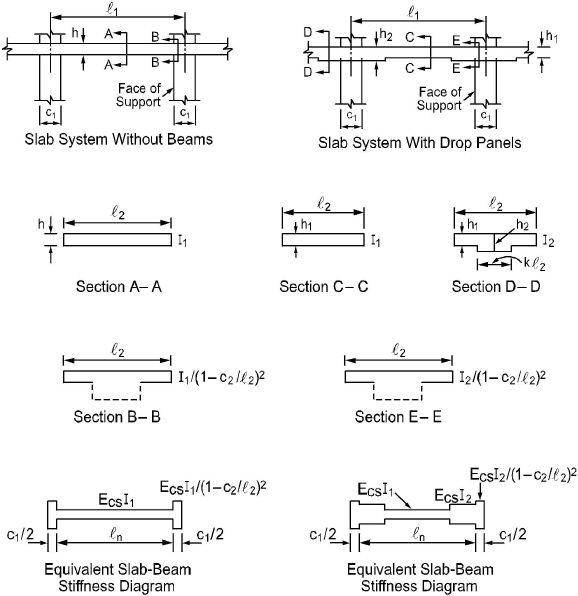
Figure 2.7 Sections for calculating slab-beam stiffness, K_sb

To account for this difference in behavior between slab structures and frames, the equivalent column torsional member, as shown in Figure 2-8, runs transverse to the direction in which the moments are being determined. The transverse slab beam can rotate even though the column may be infinitely stiff, thus permitting moment distribution between adjacent panels. It is seen that the stiffness of the equivalent column is affected by both the flexural stiffness of the columns and the torsional stiffness of the slabs or beams framing into the columns. Note that the method of computation of column stiffness is in accordance with the requirements of the code³⁹. Figure 2-10 shows a schematic representation of the stiffness of typical columns.

 

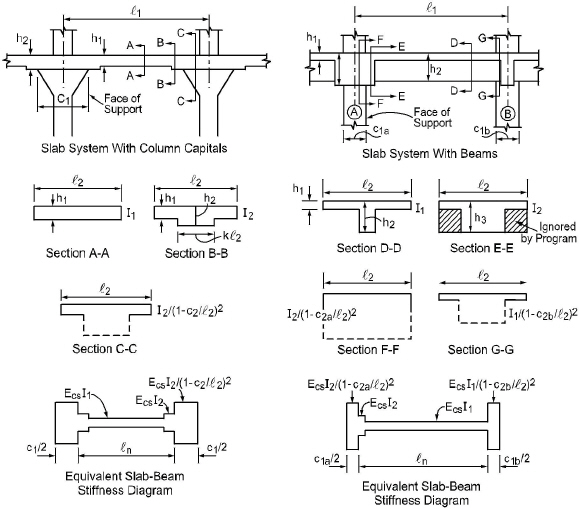
Figure 2.8 continued

The column stiffness is based on the column height, l_c, measured from mid-depth of the slab above, to the mid-depth of the slab below. spSlab calculates the stiffness of the column below the design slab, taking into account the design slab system at its top end. spSlab calculates the stiffness of the column above the design slab taking only the slab depth into account at its bottom end; column capitals, beams, or drops are ignored.

The computation of the torsional stiffness of the member requires several simplifying assumptions. The first step is to assume dimensions of the transverse torsional slab-beam members. Assumptions for dimensions of typical torsional members are shown in Figure 2-9.

The stiffness, K_t, of the torsional member is given by the following expression⁴⁰

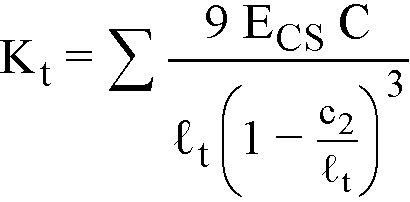      Eq. 2-20

where

S   =   denotes summation over left and right side torsional member,

E_cs   =   modulus of elasticity for slab concrete,

C   =   cross-sectional constant defined in Eq. 2-21

c₂   =   size of rectangular column or capital measured transverse to the direction in which moments are being determined,

l_t   =   l_2L and l_2R, lengths of span transverse to l₁, measured on each side of the column for ACI 318; for CSA A23.3 value of l_t is taken as the smaller of l_1a and l_2a where l_1a is the average l₁ and l_2a is the average l₂ on each side of an interior column. In case of an exterior columns, l_1a and l_2a are taken respectively as l₁ (if the column is exterior with respect to the direction of analysis) and l₂ (if column is exterior in the transverse direction) of the adjacent span, i.e. cantilevers, if any, are neglected.

 

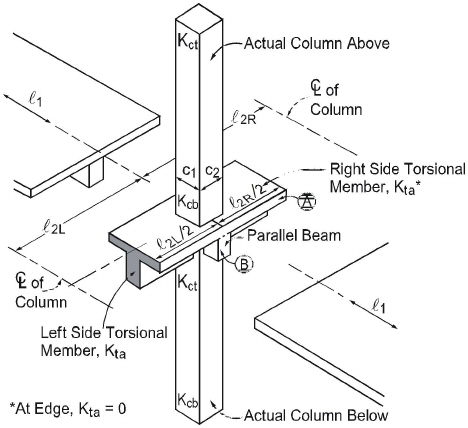
Figure 2.9 Equivalent column

The constant C is evaluated for the cross section by dividing it into separate rectangular parts and by carrying out the following summation⁴¹

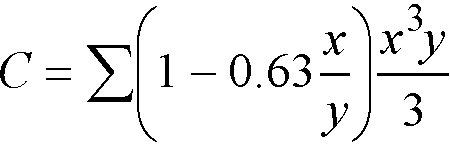      Eq. 2-21

where

x   =   short overall dimension of the rectangular part of a cross section,

y   =   long overall dimension of the rectangular part of a cross section.

The program divides the section into rectangles in such a way that the value of constant C is maximum (see Figure 2-9).

Walls perpendicular to the direction analysis can be modeled as wide columns. If a column/wall runs full length of the total design strip⁴², the program modifies moment distribution factors to achieve uniform distribution of moments along the column and middle strips. If the width of the wall is less than 75% of the total design strip then no modification of distribution factors is applied. For column/wall widths between 75% and 100% of total strip widths, moment distribution factors are linearly interpolated between regular values and uniformly distributed values.

When beams frame into the column in the direction of analysis, the value of K_t as computed in Eq. 2-20 is multiplied by the ratio of the moment of inertia of the slab with the beam (I_sb) to the moment of inertia of the slab without the beam (I_s), as shown

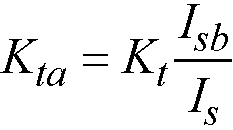      Eq. 2-22

With reference to Figure 2-8, I_s is computed from part A (slab without beam), whereas I_sb is computed from both parts A and B (slab with beam).

 

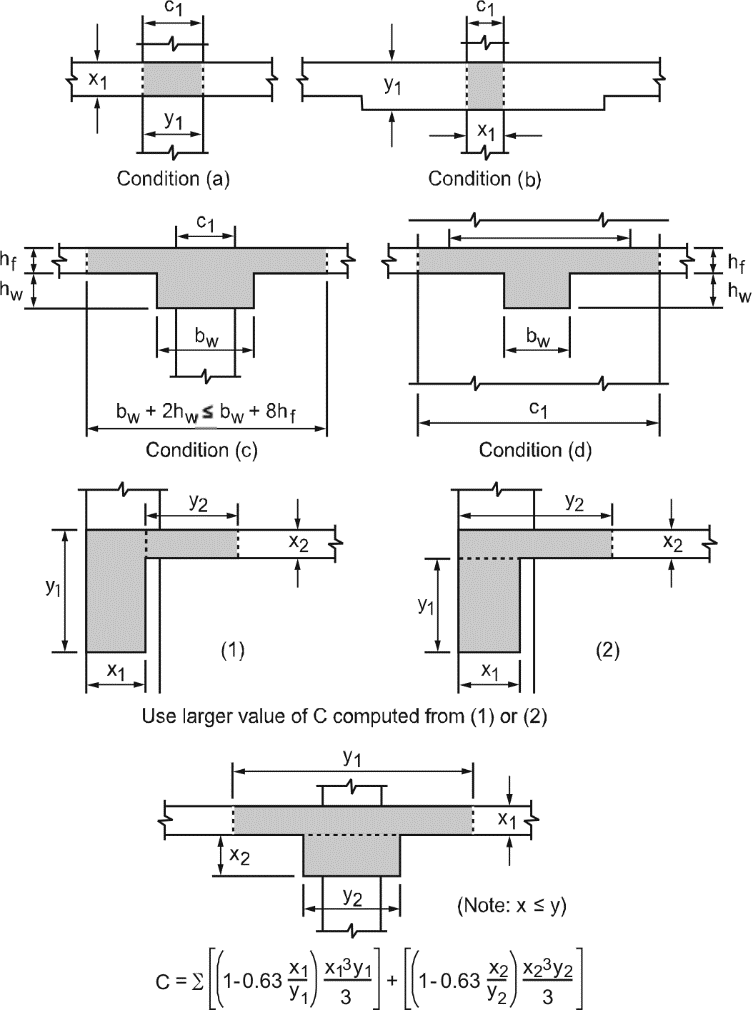
Figure 2.10 Section of the attached torsional members

 

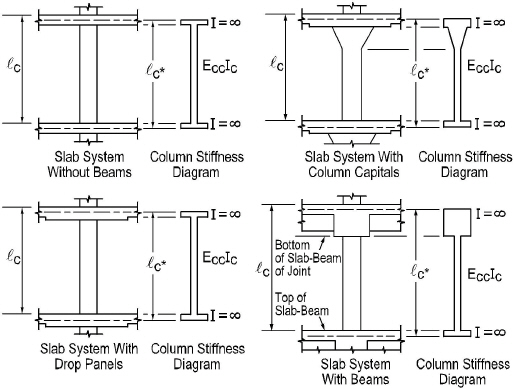
Figure 2.11 Sections for calculating the stiffness (K_c) of the column below the design floor (l_c-input, l_c*-computed)

Having the column stiffness, K_c, and the stiffness of the attached torsional member, K_t, the stiffness of the equivalent column, K_ec, is computed from the equation

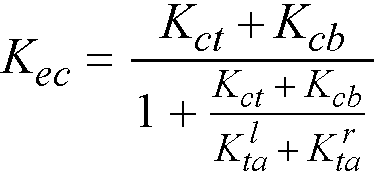      Eq. 2-23

where

K_ct   =   top column stiffness,

K_cb   =   bottom column stiffness,

K_ta   =   torsional stiffness of the left (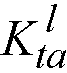) and the right (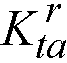) member.

2.7Loading

All applied loads are input as unfactored loads. There are no limitations imposed on the ratio of dead to live loads in the Equivalent Frame Method. Results of gravity load and lateral load analyses may be combined, however, the effects of cracking and reinforcement on stiffness must be accounted for in the lateral load analysis.

2.7.1Self-Weight

The self weight of the system is automatically calculated and assigned to the reserved load selfweight load case, SELF, which is by default defined in all new data files. The weights of the slabs, drops, and longitudinal and transverse beams are considered in the selfweight computations. Only the concrete weight is considered, the reinforcement weight is ignored. The weight of longitudinal beams is ignored starting at the column centerline, for a length equal to one-half c₁, the column dimension in the direction of analysis. This will produce slightly less self-weight than actually present for beams wider than c₂, the column’s transverse dimension.

If load case SELF is removed then the program will ignore self weight in all ultimate load combinations as well as in internally defined service load combination used to calculate displacements.

2.7.2Superimposed Loading

All superimposed vertical loading is considered to act over the entire transverse width of the slab. For slab systems with beams, loads supported directly by the beam (such as the weight of the beam stem or a wall supported directly by the beams) are also assumed to be distributed over the entire transverse width of the strip. An additional analysis may be required, with the beam section designed to carry these loads in addition to the portion of the slab moments assigned to the beam.

2.7.3Lateral Loading

For lateral loads, each frame should be analyzed as a unit for the entire height of the building (Figure 2-11). Computer programs, such as spFrame, are available for performing such analyses. It should be realized that, for lateral load analysis, slab-beam elements may have a reduced stiffness due to cracking as well as other assumptions made for the effective slab width used for the lateral analysis. The moments obtained from such an analysis may then be input into the equivalent frame model using the program to determine the appropriate design moments under combined vertical and lateral loads.

 

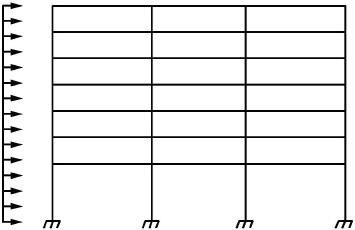
Figure 2.12 Analytical model for lateral loads

The program distributes the effect of the superimposed lateral load moments to the column strip and middle strip according to the moment distribution factors computed for gravity loads (see Table 2-2 through Table 2-4 later in this chapter).

2.7.4Load Patterns

The analysis of floor systems requires the consideration of several loading configurations. For example, the two adjacent spans loaded may produce the maximum shear stress around a column, while the alternate spans loaded may produce the maximum flexural moments. To cover different loading scenarios the program generates live load case based on the following load patterns (Figure 2-12)

•Pattern No. l (All): All spans loaded with live load,

•Pattern No. 2 (Odd): Starting at span 1, alternate spans loaded with live load,

•Pattern No. 3 (Even): Starting at span 2, alternate spans loaded with live load,

•Pattern No. 3+N (SN): Two spans adjacent to support No. N loaded with live load.

 

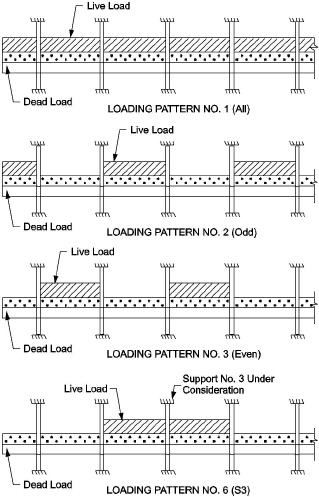
Figure 2.13 Live load patterns

The program reduces the magnitude of live load patterns No. 2 through No. (3+n) by a predefined ratio. For two-way systems, the default live load pattern ratio selected by the program equals 75% as permitted by the code⁴³. The user has the ability to select different value for the pattern ratio within the range 0-100%. If 0% is selected then load patterning effects will be neglected. However, the pattern No. 1 with all spans loaded (as specified by the user) is always considered with full unreduced magnitude.

2.7.5Load Combinations

The program allows defining up to 50 load combinations. The user has full control over the combinations. The program contains predefined (built into the program) default primary load combinations for the supported codes. These default combinations are created when starting a new project.

For the ACI 318-14, ACI 318-11, ACI 318-08, ACI 318-05, and ACI 318-02 codes, the default combinations of the Self-weight (SW), Dead (D), Live (L), Snow (S), Wind (W) and Earthquake (E) loads considered by the program are⁴⁴

U₁   =   1.4SW + 1.4D

U₂   =   1.2SW + 1.2D + 1.6L + 0.5S

U₃   =   1.2SW + 1.2D + 1.0L + 1.6S

U₄   =   1.2SW + 1.2D + 1.6S + 0.8W

U₅   =   1.2SW + 1.2D + 1.6S – 0.8W

U₆   =   1.2SW + 1.2D + 1.0L + 0.5S + 1.6W

U₇   =   1.2SW + 1.2D + 1.0L + 0.5S – 1.6W

U₈   =   0.9SW + 0.9D + 1.6W

U₉   =   0.9SW + 0.9D – 1.6W

U₁₀   =   1.2SW + 1.2D + 1.0L + 0.2S + 1E

U₁₁   =   1.2SW + 1.2D + 1.0L + 0.2S – 1E

U₁₂   =   0.9SW + 0.9D + 1.0E

U₁₃   =   0.9SW + 0.9D – 1.0E

For the ACI 318-99 code, the default combinations of the Self-weight (SW), Dead (D), Live (L), Wind (W) and Earthquake (E) loads considered by the program are⁴⁵

U₁   =   1.4SW + 1.4D + 1.7L

U₂   =   0.75(1.4SW + 1.4D + 1.7L + 1.7W)

U₃   =   0.75(1.4SW + 1.4D + 1.7L – 1.7W)

U₄   =   0.75(1.4SW + 1.4D + 1.7W)

U₅   =   0.75(1.4SW + 1.4D – 1.7W)

U₆   =   0.9 SW + 0.9D + 1.3W

U₇   =   0.9 SW + 0.9D – 1.3W

U₈   =   0.75(1.4SW + 1.4D + 1.7L + 1.7*1.1E)

U₉   =   0.75(1.4SW + 1.4D + 1.7L – 1.7*1.1E)

U₁₀   =   0.75(1.4SW + 1.4D + 1.7*1.1E)

U₁₁   =   0.75(1.4SW + 1.4D – 1.7*1.1E)

U₁₂   =   0.9 SW + 0.9D + 1.43E

U₁₃   =   0.9 SW + 0.9D – 1.43E

For the CSA A23.3-14 code load combinations are compliant with 2015 NBCC. The default combinations of the Self-weight (SW), Dead (D), Live (L), Snow (S), Wind (W) and Earthquake (E) loads considered by the program are⁴⁶

U₁   =   1.4SW + 1.4D

U₂   =   1.25SW + 1.25D + 1.5L

U₃   =   0.9SW + 0.9D + 1.5L

U₄   =   1.25SW + 1.25D + 1.5L + 1.0S

U₅   =   0.9SW + 0.9D + 1.5L + 1.0S

U₆   =   1.25SW + 1.25D + 1.5L + 0.4W

U₇   =   1.25SW + 1.25D + 1.5L – 0.4W

U₈   =   0.9SW + 0.9D + 1.5L + 0.4W

U₉   =   0.9SW + 0.9D + 1.5L – 0.4W

U₁₀   =   1.25SW + 1.25D + 1.5S

U₁₁   =   0.9SW + 0.9D + 1.5S

U₁₂   =   1.25SW + 1.25D + 1.0L + 1.5S

U₁₃   =   0.9SW + 0.9D + 1.0L + 1.5S

U₁₄   =   1.25SW + 1.25D + 0.4W + 1.5S

U₁₅   =   1.25SW + 1.25D – 0.4W + 1.5S

U₁₆   =   0.9SW + 0.9D + 0.4W + 1.5S

U₁₇   =   0.9SW + 0.9D – 0.4W + 1.5S

U₁₈   =   1.25SW + 1.25D + 1.4W

U₁₉   =   1.25SW + 1.25D – 1.4W

U₂₀   =   0.9SW + 0.9D + 1.4W

U₂₁   =   0.9SW + 0.9D – 1.4W

U₂₂   =   1.25SW + 1.25D + 0.5L + 1.4W

U₂₃   =   1.25SW + 1.25D + 0.5L – 1.4W

U₂₄   =   0.9SW + 0.9D + 0.5L + 1.4W

U₂₅   =   0.9SW + 0.9D + 0.5L - 1.4W

U₂₆   =   1.25SW + 1.25D + 1.4W + 0.5S

U₂₇   =   1.25SW + 1.25D – 1.4W + 0.5S

U₂₈   =   0.9SW + 0.9D + 1.4W + 0.5S

U₂₉   =   0.9SW + 0.9D – 1.4W + 0.5S

U₃₀   =   1.0SW + 1.0D + 1.0E

U₃₁   =   1.0SW + 1.0D – 1.0E

U₃₂   =   1.0SW + 1.0D + 0.5L + 1.0E + 0.25S

U₃₃   =   1.0SW + 1.0D + 0.5L – 1.0E + 0.25S

For the CSA A23.3-04 code load combinations are compliant with 2005 NBCC. The default combinations of the Self-weight (SW), Dead (D), Live (L), Snow (S), Wind (W) and Earthquake (E) loads considered by the program are⁴⁷

U₁   =   1.4D

U₂   =   1.25D + 1.5L

U₃   =   0.9D + 1.5L

U₄   =   1.25D + 1.5L + 0.5S

U₅   =   0.9D + 1.5L + 0.5S

U₆   =   1.25D + 1.5L + 0.4W

U₇   =   1.25D + 1.5L – 0.4W

U₈   =   0.9D + 1.5L + 0.4W

U₉   =   0.9D + 1.5L – 0.4W

U₁₀   =   1.25D + 1.5S

U₁₁   =   0.9D + 1.5S

U₁₂   =   1.25D + 0.5L + 1.5S

U₁₃   =   0.9D + 0.5L + 1.5S

U₁₄   =   1.25D + 0.4W + 1.5S

U₁₅   =   1.25D – 0.4W + 1.5S

U₁₆   =   0.9D + 0.4W + 1.5S

U₁₇   =   0.9D – 0.4W + 1.5S

U₁₈   =   1.25D + 1.4W

U₁₉   =   1.25D – 1.4W

U₂₀   =   0.9SW + 0.9D + 1.4W

U₂₁   =   0.9D – 1.4W

U₂₂   =   1.25D + 0.5L + 1.4W

U₂₃   =   1.25D + 0.5L – 1.4W + 0.5S

U₂₄   =   0.9D + 0.5L + 1.4W

U₂₅   =   0.9D + 0.5L - 1.4W

U₂₆   =   1.25D + 1.4W + 0.5S

U₂₇   =   1.25D – 1.4W + 0.5S

U₂₈   =   0.9D + 1.4W + 0.5S

U₂₉   =   0.9D – 1.4W + 0.5S

U₃₀   =   1.0D + 1.0E

U₃₁   =   1.0D – 1.0E

U₃₂   =   1.0D + 0.5L + 1.0E + 0.25S

U₃₃   =   1.0D + 0.5L – 1.0E + 0.25S

For the CSA A23.3-94 code, the default combinations of the Self-weight (SW), Dead (D), Live (L), Wind (W), Earthquake (E), and Snow (S) loads considered by the program are⁴⁸

U₁   =   1.25SW + 1.25D + 1.5L

U₂   =   1.25SW + 1.25D + 1.5L + 1.5S

U₃   =   1.25SW + 1.25D + 0.7(1.5L + 1.5W)

U₄   =   1.25SW + 1.25D + 0.7(1.5L – 1.5W)

U₅   =   1.25SW + 1.25D + 0.7(1.5L + 1.5W+ 1.5S)

U₆   =   1.25SW + 1.25D + 0.7(1.5L – 1.5W+ 1.5S)

U₇   =   1.25SW + 1.25D + 1.5W

U₈   =   1.25SW + 1.25D – 1.5W

U₉   =   0.85SW + 0.85D + 1.5W

U₁₀   =   0.85SW + 0.85D – 1.5W

U₁₁   =   1.0SW + 1.0D + 0.5L + 1.0E

U₁₂   =   1.0SW + 1.0D + 0.5L – 1.0E

U₁₃   =   1.0SW + 1.0D + 0.5L + 1.0E + 0.5S

U₁₄   =   1.0SW + 1.0D + 0.5L – 1.0E + 0.5S

U₁₅   =   1.0SW + 1.0D + 1.0E

U₁₆   =   1.0SW + 1.0D – 1.0E

2.8Column and Middle Strip Widths

The code⁴⁹ defines the width of the column strip on each side of the column centerline as being one-fourth of the smaller of either the transverse or the longitudinal span. These widths are printed as part of the design results.

The strip widths at a support are computed by (see Figure 2-13)

•column strip

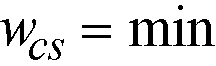
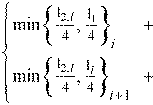
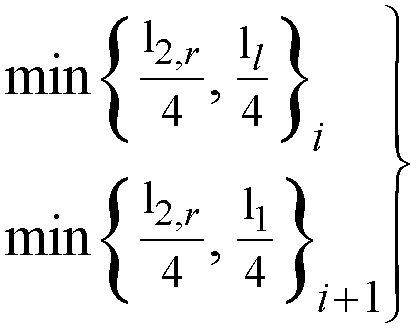      Eq. 2-24

•middle strip

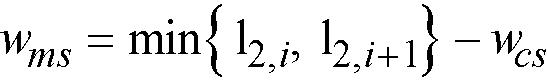      Eq. 2-25

 

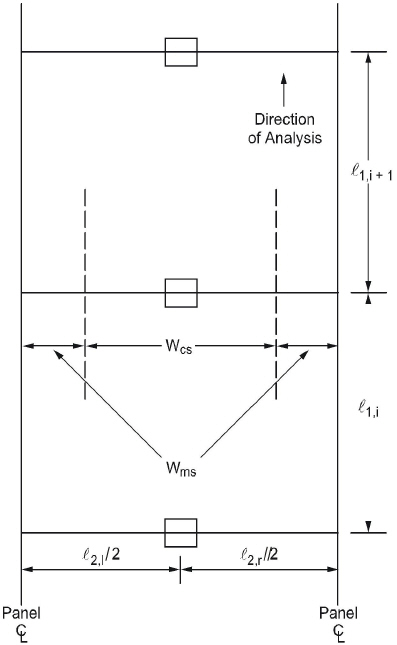
Figure 2.14 Strips widths at support

The strip widths in the span are defined as (see Figure 2-14)

•column strip

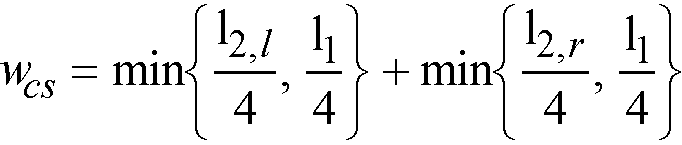      Eq. 2-26

•middle strip

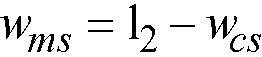      Eq. 2-27

where

l₁   =   span length in the direction of analysis,

l_2,l   =   the input transverse strip widths on the left of column centerline,

l_2,r   =   the input transverse strip widths on the right of column centerline,

l₂   =   l_2,l/2 + l_2,r/2, the total input transverse strip width.

 

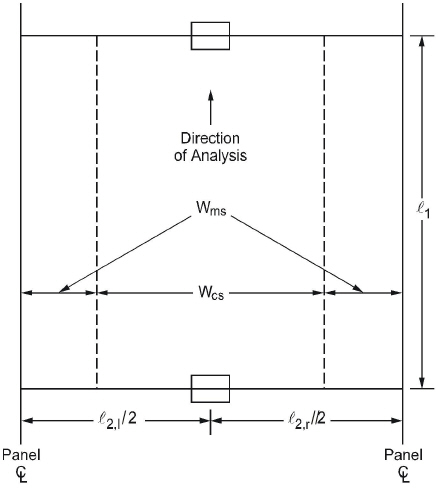
Figure 2.15 Strip widths in span

If a longitudinal slab band is defined (CSA A23.3-14/04 standard only) then the column strip width is automatically adjusted to be equal to the band width

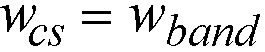      Eq. 2-28

If a longitudinal beam exists then the adjusted column strip width, 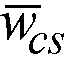, is calculated by subtracting the beam width, w_beam, from the width of the column strip

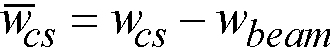      Eq. 2-29

If the user selects the Beam T-Section Design option in Solve Options, the beam width, w_beam, used by the program will include portion of the slab on each side of the beam equal to projection of the beam below the slab, but not greater than slab thickness⁵⁰. Otherwise, only web width is used. If the beam width, w_beam, is greater than the column strip width, w_cs, then the adjusted column strip width is set to zero and moment distribution factors are adjusted to apply all column strip moment to the beam. This may occur when modeling a slab band with a wide longitudinal beam for codes other than CSA A23.3-14/04. In case of CSA A23.3-14/04 standard, the dedicated Longitudinal Slab Band option in General Information dialog window is available to model slab band systems explicitly.

By selecting User Slab Strip Width and User Distribution Factors options in Solve Options dialog window, the user has the ability to manually override strip widths and moment distribution factors calculated automatically by the program and requires engineering judgment.

Note: For exterior frames, the edge width should be specified to the edge of the slab from the column centerline. Entering edge width greater than l₁/4 involves engineering judgment regarding two-way behavior of the system and the applicability of the equivalent frame method.

2.9Strip Design Moments

For design purposes⁵¹, spSlab considers negative moments as those producing tension at the top of the slab and positive moments as those producing tension at the bottom of the slab. The negative design moment is taken at the face of the column below the slab, or at the face of the column capital, but in no case is it considered at a location greater than 0.175 of the longitudinal span length, l₁, away from the center of the column.⁵² This imposes a limit on long narrow supports, in order to prevent undue reduction in the design moment. For slab systems with transverse beams, the face of a beam is not considered as the face of support. For end columns with capitals, the negative moments are taken at the midpoint of the capital extension.⁵³ If a positive moment occurs at a support then its value at the face of the column above the slab is considered (or at the support centerline if there is no column above the slab).

spSlab computes the amount of reinforcement for the moments on the left and the right side of the support. The negative design moment is the moment which requires the most area of reinforcement to be resisted. The location, left or right of the support, of the maximum moment may vary when systems differ on each side of the support (for example, a system with beams on one side only).

spSlab automatically calculates the values of strip moment distribution factors for column strips and longitudinal beams (if present). Portion of the total factor moment not assigned to a column strip or a beam is then proportionally assigned to the remaining middle strip.

Note: By checking User Distribution Factors option in Solve Options dialog window, the user has the ability to manually adjust strip moment distribution factors calculated automatically by the program.

2.9.1ACI 318 and CSA A23.3-94⁵⁴

The column strips are proportioned to resist the portions in percent of interior negative factored moments according to Table2-2.⁵⁵

Table 2.2 Column Strip Percent of Interior Negative Factored Moments at Supports

The column strips are proportioned to resist the portions in percent of exterior negative factored moments according to Table 2-3.⁵⁶

Table 2.3 Column Strip Percent of Exterior Negative Factored Moments at Supports

The values α₁ in Table 2-2 and Table 2-3 and β_t in Table 2-3 are defined as

α_f1   =   ratio of flexural stiffness of the beam section to flexural stiffness of a width of slab bounded by centerlines of adjacent panels (if any) on each side of the beam in the direction of analysis. For flat plates, flat slabs, and waffle (a_f1 l₂/l₁) = 0

β_t   =   ratio of torsional stiffness of an edge beam section to flexural stiffness of a width of slab equal to the span length of the beam, center-to-center of supports.⁵⁷ When no transverse beams are present, β_t = 0, otherwise

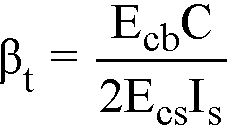      Eq. 2-30

where

E_cb   =   modulus of elasticity of beam concrete,

E_cs   =   modulus of elasticity of slab concrete,

C   =   cross-sectional constant, see Eq. 2-21

I_s   =   moment of inertia of the gross section of the slab about its centroidal axis.

For intermediate values of (l₂/l₁), (a_f1l₂/l₁) and β_t the values in Table 2-2 and Table 2-3 are interpolated using equations Eq. 2-31 and Eq. 2-32.

Percentage of negative factored moment at interior support to be resisted by column strip

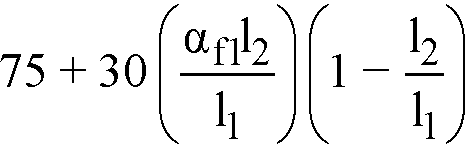      Eq. 2-31

Percentage of negative factored moment at exterior support to be resisted by column strip

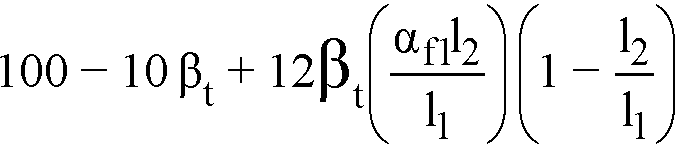      Eq. 2-32

When a column width, c₂, is equal to or greater than 75 percent of the tributary strip width l₂, the distribution factor for negative column strip moment is linearly interpolated between the factor for regular support, and the factor equal 0.50 (moment uniformly distributed across l₂). This extends the requirement of the design code⁵⁸, by providing continuous linear transition between standard and uniform moment distributions, depending on the relative dimension of the support with respect to strip width. User may override software assumptions by selecting user defined distribution factors.

When designing by the CSA A23.3-94 code, a portion of the total positive or interior negative moment equivalent to⁵⁹

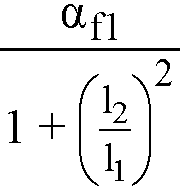      Eq. 2-33

is resisted by the beam. For exterior supports, the beam is proportioned to resist 100% of the negative moment.

That portion of the moment not resisted by the beam is resisted by the slab. The reinforcement required to resist this moment is distributed evenly across the slab.

For ACI designs the longitudinal beams are proportioned to resist 85 percent of the column strip moments if a_f1l₂/l₁ is equal to or greater than 1.0. For values of a_f1l₂/l₁ between 0 and 1.0, the beam is designed to resist a proportionate percentage of the column strip moment between 0 and 85.⁶⁰

The middle strips are proportioned to resist the portion of the total factored moments that is not resisted by the column strips.

The column strips are proportioned to resist the portions in percent of positive factored moments according to Table 2-4.⁶¹

For intermediate values of (l₂/l₁) and (a_f1l₂/l₁) the values in Table 2-4 are interpolated using Eq. 2-34 follows

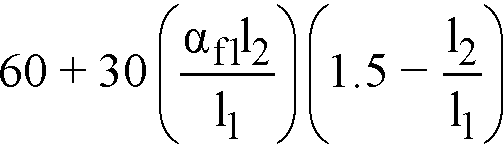      Eq. 2-34

Note: For flat plates, flat slabs, and waffle slabs, a_f1l₂/l₁ = 0.

2.9.2CSA A23.3-14/04

For slabs without drop panels (with or without transverse beams) the following moment factors are used⁶²

•Negative moment at interior column, factor = 0.80

•Negative moment at exterior column, factor = 1.00

•Positive moment at all spans, factor = 0.60

For slabs with drop panels (with or without transverse beams) the following moment factors are used⁶³

•Negative moment at interior column, factor = 0.825

•Negative moment at exterior column, factor = 1.00

•Positive moment at all spans, factor = 0.60

For slabs with longitudinal slab bands⁶⁴

•Negative moment at interior column, factor = 0.90

•Negative moment at exterior column, factor = 1.00

•Positive moment at all spans, factor = 0.90

For slabs with transverse slab bands⁶⁵

•Negative moment at interior column in width b_b, factor from 0.05 to 0.15 range is selected so that the remaining moment is distributed evenly over the entire frame width (including b_b width) and at least one-third of the total factored moment⁶⁶ is applied to the band width b_b.

•Negative moment at exterior column, factor = 1.00

•Positive moment at all spans where (l₁/l₂) ≥ 1.0, factor = 0.55

•Positive moment at all spans where (l₁/l₂) < 1.0, factor = 0.55 (l₁/l₂)

For slabs with beams between all the supports⁶⁷, the positive and interior negative factored moments are distributed as follows

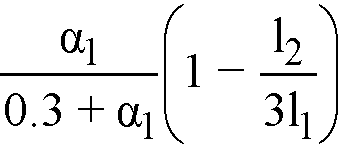      Eq. 2-35

Factored negative moments at exterior supports are assigned in 100% proportion to beams.

CSA A23.3-14/04 does not stipulate requirement for distributing moments in slab systems with beams between some (but not all) supports. For estimation of the moment resisted by the beams in this case, the program applies the ACI approach described in the previous section where longitudinal beams are proportioned to resist 85 percent of the column strip moments if a_f1l₂/l₁ is equal to or greater than 1.0. For values of a_f1l₂/l₁ between 0 and 1.0, the beam is designed to resist a proportionate percentage of the column strip moment between 0 and 85%.

2.10Moment Redistribution

Redistribution of negative moments applies to one-way and beam systems only. It can be engaged using the Input Redistribution option on the Solve Options tab in the General Information dialog box.

The program allows for redistribution of negative moments at supports. Only reduction in negative moments is considered. Increase of negative moments at the support is not taken into account even though it is allowed by the code⁶⁸. Static equilibrium is maintained meaning that bending moments and shear forces along the span are adjusted in accordance with the reduction of moments applied at the supports. The following procedure is followed to obtain moment redistribution factors at the supports.

From elastic static analysis, the largest moments from all load combinations and load patterns are determined at support faces on both ends of each span except cantilevers. These moments are used to calculate the maximum percentage adjustment of moments, 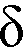, allowed by the codes.

For ACI 318-14, ACI 318-11, ACI 318-08, ACI 318-05, and ACI 318-02⁶⁹

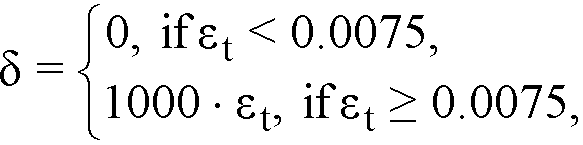      Eq. 2-36

where ε_t is net tensile strain in extreme tension steel at nominal strength.

For ACI 318-99⁷⁰

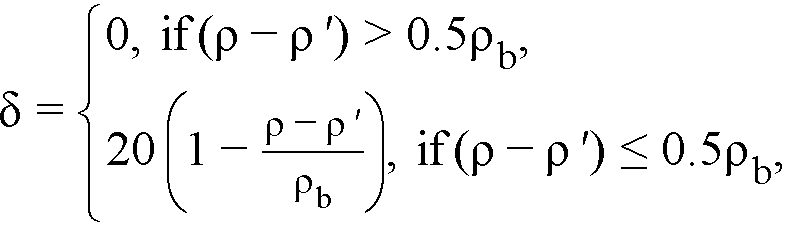      Eq. 2-37

where

ρ   =   tension reinforcement ratio,

ρ'   =   compression reinforcement ratio,

ρ_b   =   balanced reinforcement ratio.

For CSA A23.3⁷¹

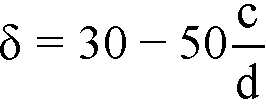      Eq. 2-38

where

c   =   distance from extreme compression fiber to neutral axis,

d   =   distance from extreme compression fiber to centroid of tension reinforcement.

In the investigation mode, program uses the area of provided reinforcement to obtain redistribution factors. In the design mode the required reinforcement area is used. Additionally, 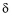 is limited to 20% and not to exceed the maximum values specified by the user. Negative moments at span ends are reduced by the amount of redistribution factors and new moment values are iteratively used to obtain new redistribution factors. This iterative procedure is repeated until the change in distribution factor is negligible (does not exceed 0.01%), but no more than 10 times.

2.11Shear Analysis of Slabs

Shear analysis in spSlab takes into account one way shear and two-way shear. For two-way shear, the program considers contributions of factored shear force⁷², V_u, and fraction of unbalanced moment transferred by shear⁷³, g_vM_unbal. spSlab does not consider torsional stresses in the slab. If in the engineer’s judgment this may control, it must be computed manually.

spSlab checks one-way shear at a critical section located at a distance not less than the effective depth away from the face of the support⁷⁴. If a concentrated load is applied closer than the effective depth away from the face of the support then critical section is located at the face of the support. Factored shear force at the critical section is obtained from the analysis of the equivalent frame⁷⁵.

 

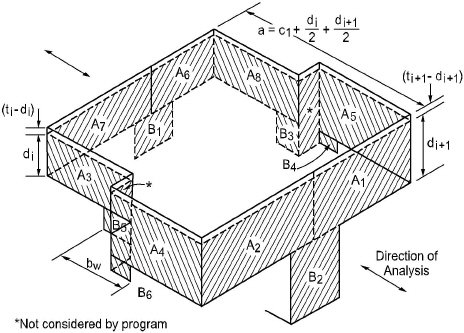
Figure 2.16 Critical section for two-way shear

Figure 2-15 shows the general two-way shear area⁷⁶ used by spSlab. Note that the shaded area represents the general case and is modified for special considerations as explained below.

Beams are considered in the two-way shear as indicated in Figure 2-15 by areas B₁, B₂, B₃, B₄, B₅, and B₆. Ordinarily, transverse beams transfer unbalanced moment to the column through torsion along the beam and not through shear between the slab and column. However, the code leaves the transfer method to the engineer’s judgment concerning the point at which punching shear is no longer applicable and beam shear becomes the dominate element in shear transfer to the column. spSlab makes no such distinction and computes unbalanced moment transfer stress without regard to any beams framing into the column. When a beam is present, the depth of the beam increases the depth of the critical section where it intersects with the beam. The distances from the face of the support to the critical section will also be increased, i.e. effective depth of the beam will be used to calculate the distance instead of effective depth of the slab, if it results in a critical section that is still within the beam. Otherwise, distances to the critical section are not increased.

For circular supports (column or column capital), ACI code and CSA standard differ in their treatment and do not provide clear guidance towards the applicability of an equivalent rectangular section for checking punching shear around circular supports. Therefore, spSlab provides as a default option the calculation of properties of the critical section for punching shear based on circular critical shear perimeter. This option is possible given that both the soffit around the perimeter of circular support and the soffit around the perimeter of circular critical shear perimeter are flat & critical shear perimeter stays circular.

If circular critical shear perimeter is not achievable or possible, then, the program calculates properties of the critical section for punching shear based on an equivalent rectangular support with the same centroid and equal perimeter length⁷⁷. The equivalent rectangular support is a square with side length equal to p D/4 » 0.785 D where D is the diameter of the circular support as shown in Figure 2-15.

 

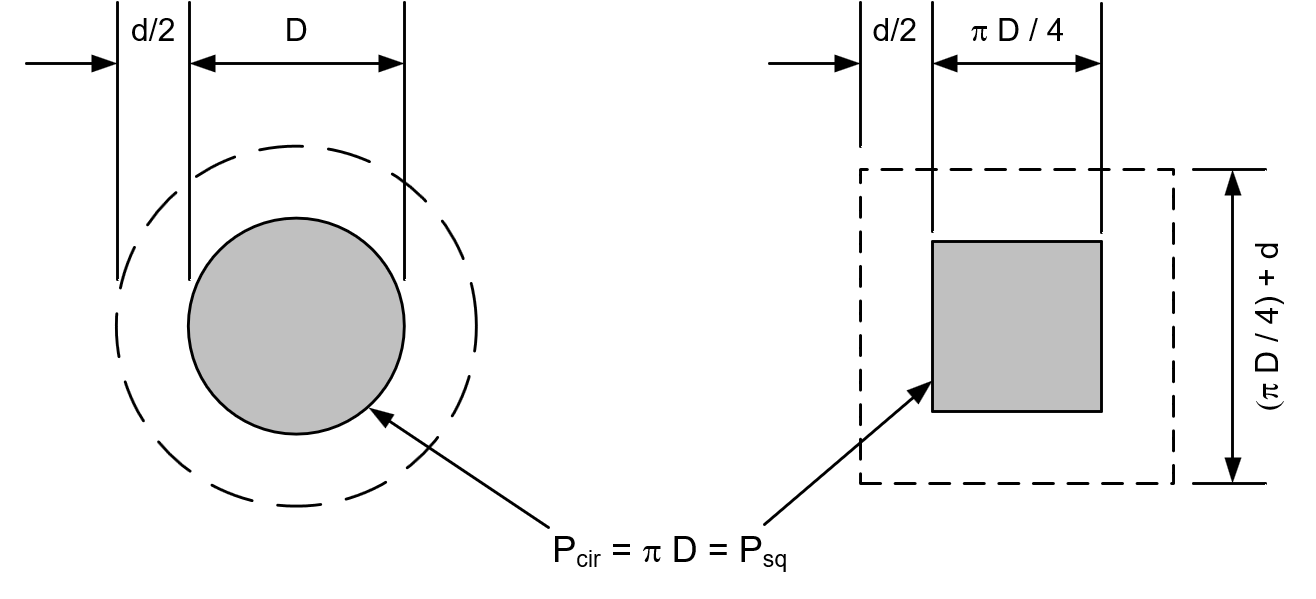
Figure 2.17 Critical section for circular column

While this approach is widely used, it produces an equivalent section but not an equivalent shear perimeter. It is, therefore, left to the end-user discretion to judge the use of the circular shear perimeter as it produces more conservative results compared with the traditional equivalent square option.

The critical section is considered closed if the concrete slab around a column extends to a distance greater than or equal to the specified threshold value. In spSlab, the user may define the distance extended beyond the column face in order to consider the section closed. If the critical section does not meet the distance requirement, it is considered open.

ACI 318-08 code introduced the definition of the shear cap⁷⁸ which, alternatively to column capital, can be used to increase the critical section around the column. spSlab users can use the capital geometry to model a shear cap and calculate the punching shear through the thickness of the slab itself (shear cap acting as capital). Other failure modes, such as punching within the perimeter of the shear cap, need to be verified by the user manually. The dimensions of the substitute capital have to be selected such that the resulting critical section is equivalent to critical section for a column with a shear cap. ACI code⁷⁹ requires shear caps to extend beyond the face of the column by at least the distance equal to cap depth, and so depth/extension ratio should not exceed 1.0. For column capitals depth/extension ratio should not be less than 1.0. Therefore to model shear cap acting as capital, the substituted capital should have depth/extension ratio equal to 1.0.

2.11.1Critical Section for Interior Supports of Interior Frames

The critical section (Figure 2-17) consists of four vertical surfaces through the slab, located at distances of d/2 beyond the support faces.

The critical section for interior supports of interior frames is always closed. A closed section will have all its faces defined in Figure 2-15 resisting shear as indicated by Eq. 2-39

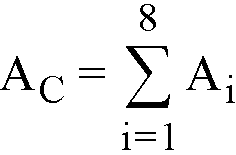      Eq. 2-39

If beams frame⁸⁰ into the column, then the critical section includes the dimensions of the beams (B₁ through B₆ in Figure 2-15).

 

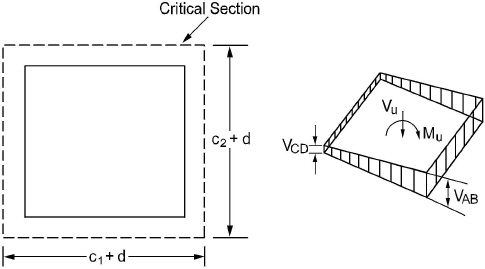
Figure 2.18 Interior supports of interior frames

2.11.2Critical Section for Exterior Supports of Interior Frames

The critical section for exterior supports of interior frames (Figure 2-18) will be either closed (full A₇ and A₆ for the first column or A₁ and A₂ for the last column in Figure 2-15) or open, depending upon the length of the cantilever in relation to slab thickness. The critical section will be considered closed when the clear cantilever span, l_c, is greater than or equal to the distance defined by the user beyond the column face. The default value of the distance is 4 h when an ACI code is selected⁸¹ and 5 d for the CSA standard⁸². The user can modify the default value to accommodate scenarios when larger distances are required, e.g. 10 h for slabs with openings⁸³. If beams frame into the column then the critical section includes the contributions from the beam dimensions (B₁ through B₆ in Figure 2-16).

 

Figure 2.19 Exterior supports of interior frames

2.11.3Critical Section for Interior Supports of Exterior Frames

Figure 2-19 shows the critical section for shear for an interior support of an exterior frame. Note that the section is considered as U-shaped (A₅ = 0, A₈ = 0, B₃ = 0, B₄ = 0 in Figure 2-15) and it extends up to the edge of the exterior face of the support. If beams frame into the column, then the critical section includes the contribution from the beam dimensions (B₁ through B₆ in Figure 2-15). If the exterior cantilever span, l_c, is greater than or equal to the distance defined by the user beyond the column face (the default value is 4 h when an ACI code is selected⁸¹ and 5 d for the CSA standard⁸²), the section is treated as closed, that is, the support is treated as an interior support of an interior frame.

2.11.4Critical Section for Exterior Supports of Exterior Frames

The critical section for an exterior support of an exterior frame will typically be L-shaped (A₅ = 0, A₆ = 0, A₇ = 0, A₈ = 0, B₁ = 0, B₃ = 0, and B₄ = 0 in Figure 2-15).

If the cantilever span, l_c, (in the direction of analysis) is greater than or equal to the distance defined by the user beyond the column face (the default value is 4 h when an ACI code is selected⁸¹ and 5 d for the CSA standard⁸²), then the section is treated as a U-shaped interior support. If, in addition, the cantilever span in transverse direction is greater than or equal to the distance defined by the user beyond the column face, the section is treated as closed. If beams frame into the column, then the critical section includes the contributions from the beam dimensions.

 

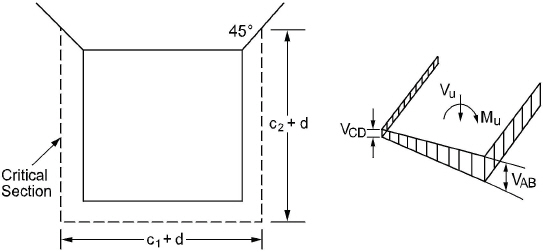
Figure 2.20 Interior supports of exterior frames

2.11.5Computation of Allowable Shear Stress at Critical Section

One-way shear strength of slabs is limited⁸⁴ to 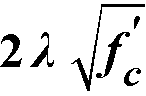. Two-way shear strength of slabs is affected by concrete strength, relationship between size of loaded area and slab thickness, loaded area aspect ratio, and shear-to-moment ratio at slab-column connections.

These variables are taken into account in the allowable shear stress, v_c, computed at distances of d/2 around the columns and drops (if applicable). For the ACI 318 code, v_c is taken as the smallest of the 3 quantities⁸⁵

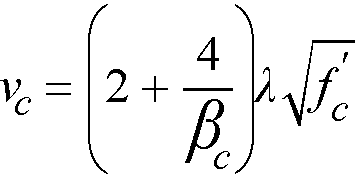      Eq. 2-40

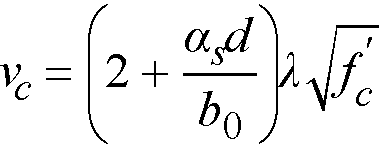      Eq. 2-41

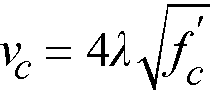      Eq. 2-42

where

β_c   =   the ratio of the long to the short side of the column.

α_s   =   a constant dependent on the column location, (40 for an interior 4-sided effective critical area, 30 for an exterior 3-sided critical area, 20 for a corner 2-sided effective critical area.)

d   =   distance from the slab bottom to centroid of the slab tension reinforcement at support (average value is used if d changes along critical section perimeter)

b₀   =   the perimeter of the critical section

l   =   factor⁸⁶ reflecting the reduced mechanical properties of lightweight concrete equal to 0.75 for all-lightweight concrete, 0.85 for sand-lightweight concrete and 1.0 for normal weight concrete. Refer to Table 2-1 for determination of concrete type.

For the CSA A23.3⁸⁷, the allowable shear stresses are calculated as the minimum of the following metric equations

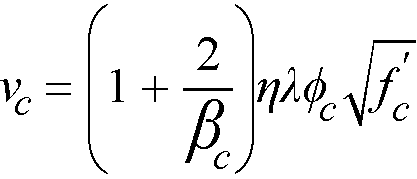      Eq. 2-43

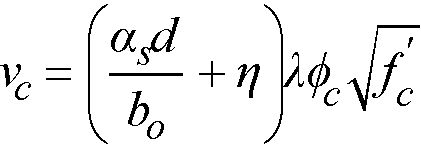      Eq. 2-44

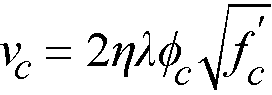      Eq. 2-45

where

h   =   0.19 for CSA A23.3-14/04 and 0.20 for CSA A23.3-94

α_s   =   a constant dependent on the column location, (4 for an interior 4-sided effective critical area, 3 for an edge column, 2 for a corner column)

d   =   distance from the slab bottom to centroid of the slab tension reinforcement at support (average value is used if d changes along critical section perimeter)

φ_c   =   resistance factor for concrete⁸⁸ equal to 0.60 for CSA A23.3-94 and for CSA A23.3-14/04 it is equal to 0.65 for regular and 0.70 for precast concrete

l   =   factor⁸⁹ reflecting the reduced mechanical properties of lightweight concrete equal to 0.75 for structural low-density concrete, 0.85 structural semi-low-density concrete and 1.0 for normal density concrete. Refer to Table 2-1 for determination of concrete type.

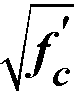   ≤   8 MPa.

When the value of d is greater than 300mm, allowable stress v_c obtained from the above three equations shall be multiplied by 1300/(1000+d) as required by CSA A23.3-14/04 code⁹⁰.

The allowable shear stress around drops when waffle slabs are used is computed as

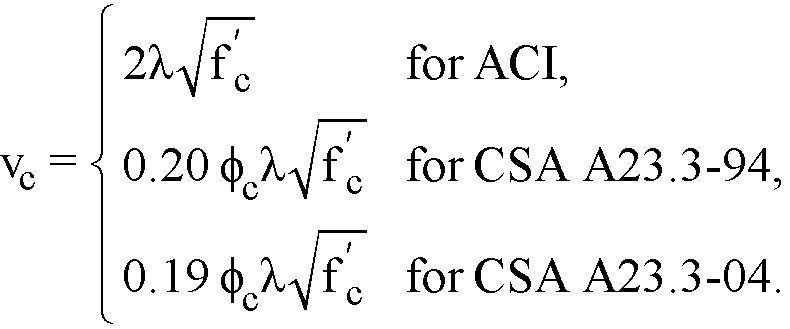      Eq. 2-46

For waffle slab systems with valid ribs defined earlier in this chapter, the allowable shear stress is increased by 10% for ACI designs.⁹¹ 

2.11.6Computation of Factored Shear Force at Critical Section   

The factored shear force V_u in the critical section, is computed as the reaction at the centroid of the critical section (e.g., column centerline for interior columns) minus the self-weight and any superimposed surface dead and live load acting within the critical section. If the section is considered open, two 45 degree lines are drawn from the column corners to the nearest slab edge (lines AF and DE in Figure 2-19) and the self-weight and superimposed surface dead and live loads acting on the area ADEF are omitted from V_u.

2.11.7Computation of Unbalanced Moment at Critical Section

The factored unbalanced moment used for shear transfer, M_unbal, is computed as the sum of the joint moments to the left and right. Moment of the vertical reaction with respect to the centroid of the critical section is also taken into account by

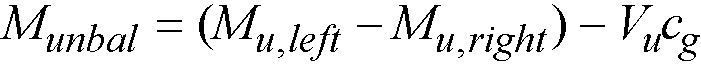      Eq. 2-47

where

M_u,left   =   factored bending moment at the joint on the left hand side of the joint,

M_u,right   =   factored bending moment at the joint on the right hand side of the joint,

V_u   =   factored shear force in the critical section described above,

c_g   =   location of the centroid of the critical section with respect to the column centerline (positive if the centroid is to the right in longitudinal direction with respect to the column centerline).

2.11.8Computation of Shear Stresses at Critical Section

The punching shear stress computed by the program is based on the following⁹²

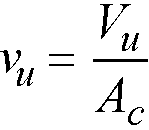      Eq. 2-48

where

V_u   =   factored shear force in the critical section described above,

A_c   =   area of concrete, including beam if any, resisting shear transfer.

Under conditions of combined shear, V_u, and unbalanced moment, M_unbal, γ_vM_unbal is assumed to be transferred by eccentricity of shear about the centroidal axis of the critical section. The shear stresses computed by the program for this condition correspond to⁹³

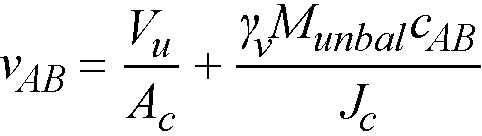      Eq. 2-49

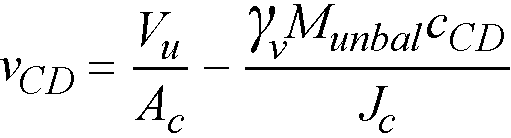      Eq. 2-50

where

M_unbal   =   factored unbalanced moment transferred directly from slab to column, as described above,

γ_v   =   (1 - γ_f)   Eq 2-51

      is a fraction of unbalanced moment considered transferred by the eccentricity of shear about the centroid of the assumed critical section,⁹⁴ 

c   =   distance from centroid of critical section to the face of section where stress is being computed,

J_c   =   property of the assumed critical section analogous to polar moment of inertia.

Factor γ_f in Eq. 2-51 is calculated as⁹⁵

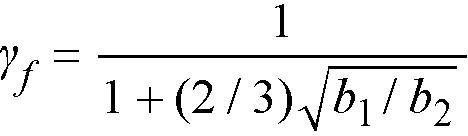      Eq. 2-52

where

b₁   =   width of critical section in the direction of analysis,

b₂   =   width of the critical section in the transverse direction.

If an ACI 318 standard is selected then the program provides an option to use an increased value⁹⁶ of γ_f. For edge and corner columns with unbalanced moment about an axis parallel to the edge, the value can be increased to 1.0 if the factored shear force at the support doesn’t exceed 0.75fV_c for edge columns and 0.5fV_c for corner columns. For ACI 318-99, ACI 318-02, and ACI 318-05, condition that reinforcement ratio in the effective slab width doesn’t exceed 0.375r_b must also be satisfied to apply the increase. For interior columns and for edge columns with unbalanced moment perpendicular to the edge, g_f can be increased 25% but the final value of g_f cannot exceed 1.0. The increase can be applied if the shear doesn’t exceed 0.4fV_c. Also, the net tensile strain in the effective slab has to exceed 0.010 for the ACI 318-08, ACI 318-11, and ACI 318-14. For earlier ACI 318 editions, the condition that reinforcement ratio does not exceed 0.375r_b applies.

spSlab calculates v_u as the absolute maximum of v_AB and v_CD. Local effects of concentrated loads are not computed by spSlab and must be calculated manually.

2.11.9Shear Resistance at Corner Columns

For the CSA A23.3 code in design mode, the program performs one-way shear resistance check in the vicinity of corner columns. A corner column is determined in spSlab as the exterior support along an exterior left or exterior right equivalent frame. For slabs with edge beams or drop panels a supplementary check including the contribution of these components should be performed manually.

For the CSA A23.3-94 edition, a critical shear section is located d/2 from the column corner. The minimum length section is selected using an optimization algorithm which analyzes sections at different angles. The extension to the cantilevered portion is considered by a length not to exceed effective slab thickness d.

For the CSA A23.3-14/04 edition, a critical shear section is located not further than d/2 from the edge of the column or column capital. The extension to the cantilevered portion is considered by a length not to exceed effective slab thickness d. The factored shear resistance is calculated as follows⁹⁷

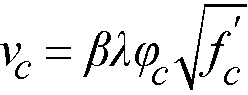      Eq. 2-53

where

β   =   factor accounting for shear resistance of cracked concrete⁹⁸

2.11.10Shear Resistance in Slab Bands

When performing two-way shear analysis for models with non-continuous longitudinal slab bands a non-standard partial drop panel is anticipated to close the slab band and the calculations are performed as follows. Punching shear around the column is checked using effective depth of the slab band on one side of the column and the depth of the extension drop panel on the other side of the column. On each four sides of the column the critical section is located ½ of the respective depth from the face of the column. Punching shear calculation around the drop panel/slab band assumes that the plane of critical section, which cuts perpendicularly through slab band, is located ½d of the slab band from the face of column. For three remaining column faces critical section is located ½d of the slab measured from the respective edges of drop panel or slab band.

2.12One-Way Shear Analysis of Longitudinal Beams and Slabs

When longitudinal beams are present in a span, the program computes the shear reinforcement requirements for the beams. Table “Longitudinal Beam Shear Reinforcement Required” in the program output provides values of V_u, V_c, and Av/s for selected segment locations of each span. Segment lengths are chosen not to exceed the beam section depth. The beginning of first segment and the end of last segment correspond to the locations of critical sections on the left and right support respectively. The critical sections are located at a distance d, the effective beam depth, away from the column face at both the left and the right ends of the beam. However, if concentrated loads are present within distance d from the column face, critical section is selected at the column face.

V_u is computed from the load acting over the entire width of the design strip. The program makes no distinction between shallow beams (a_f1l₂/l₁ < 1) and deeper beams (a_f1l₂/l₁ > 1).

2.12.1Shear Calculations for ACI 318 and CSA A23.3-94

Shear strength provided by concrete, V_c, is computed by⁹⁹

 

where

f_c   =   resistance factor for concrete¹⁰⁰ equal to 0.60.

In CSA A23.3-94 design, for beams without minimum stirrup reinforcement and greater than 300 mm deep, V_c is calculated from the following equation¹⁰¹

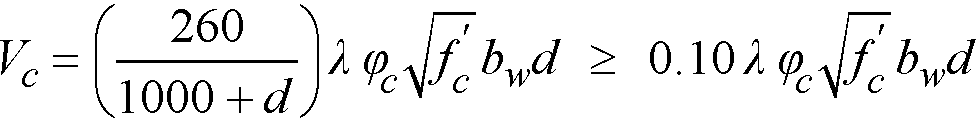      Eq. 2-55

When 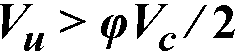, the beam must be provided with at least a minimum shear reinforcement of¹⁰²

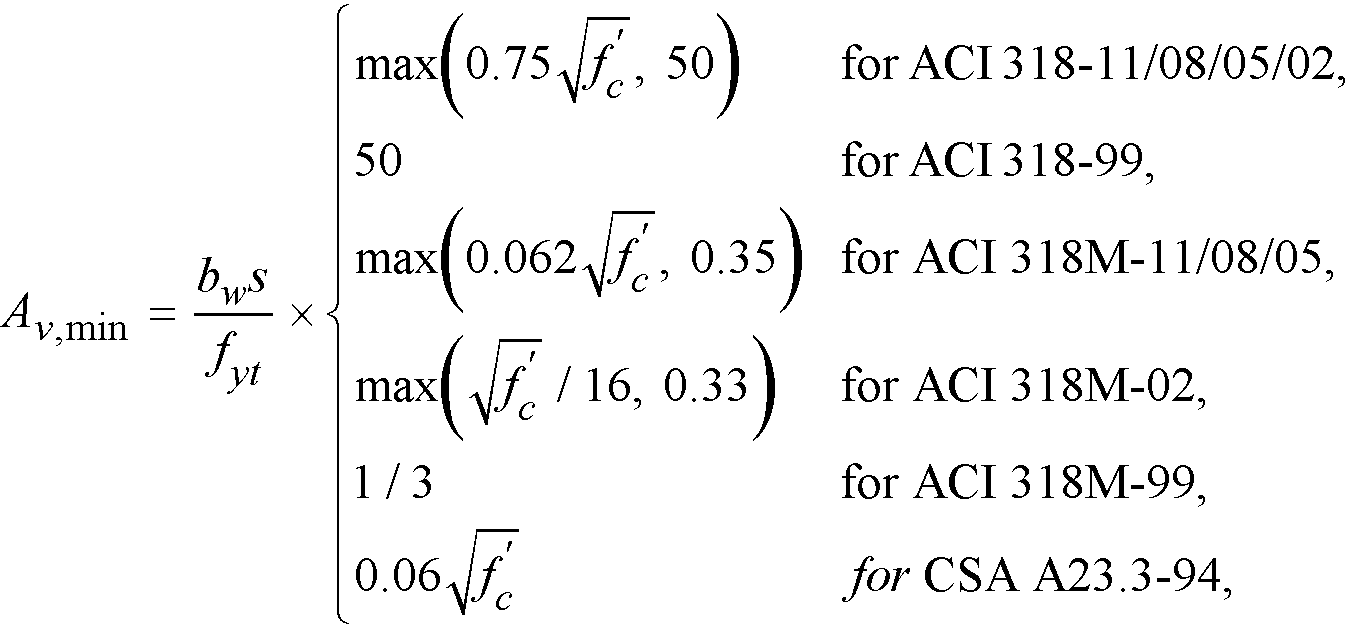      Eq2-56

where

A_v   =   area of all stirrup legs,

s   =   stirrups spacing,

b_w   =   longitudinal beam width,

f_yt   =   yield strength of the shear reinforcement.

In the investigation mode, if the ACI-318 spacing requirement for shear reinforcement¹⁰³ or minimum shear reinforcement requirement are not met, the shear strength of the section is taken as one-half of the shear strength provided by concrete.

When 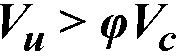, shear reinforcement must be provided so that

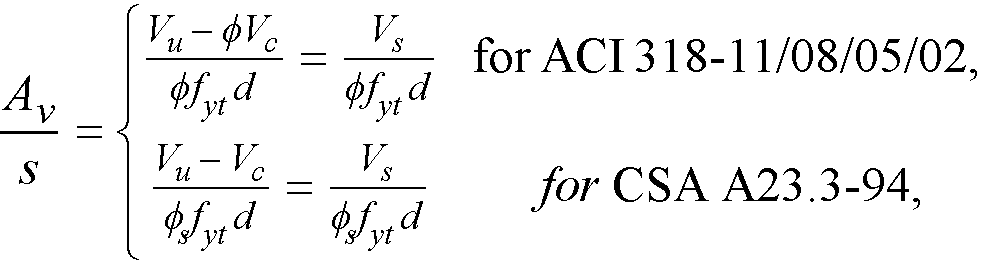      Eq. 2-57

where

V_u   =   factored shear force at the section being considered

V_s   =   shear strength provided by shear reinforcement

d   =   effective depth of the beam at the same location

f   =   strength reduction factor for shear calculations¹⁰⁴ equal to 0.85 for ACI 318-99 and equal to 0.75 for ACI 318-14, ACI 318-11, ACI 318-08, ACI 318-05, and ACI 318-02

f_s   =   resistance factor for reinforcement¹⁰⁵ equal to 0.85

The capacity of shear reinforcement V_s is limited to 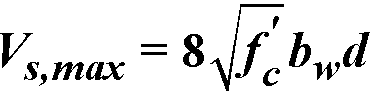( 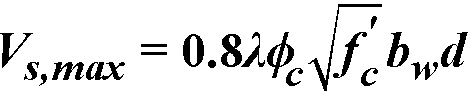for CSA A23.3-94). When V_u exceeds fV_c+ fV_s,max (V_c+ V_s,max for CSA A23.3-94), the beam section dimensions must be increased or a higher concrete strength must be provided.¹⁰⁶ 

When 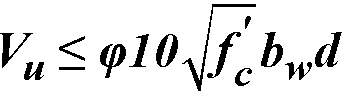, the spacing is computed as

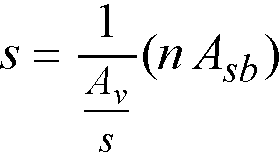      Eq. 2-58

where

A_sb   =   stirrup bar area (one leg)

n   =   number of stirrup legs

The maximum stirrup spacing for ACI codes¹⁰⁷ must not exceed d/2 or 24 in when 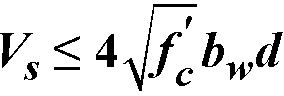. . 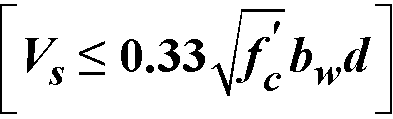When 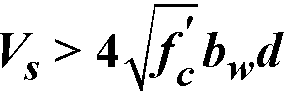, the maximum stirrup spacing must be reduced by half, to d/4 or 12 in. For the CSA A23.3-94 standard¹⁰⁸, maximum spacing must not exceed the smaller of 0.7 d and 600 mm when  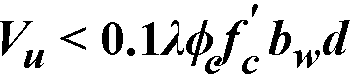or the smaller of 0.35 d and 300 mm when .

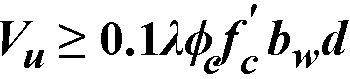When 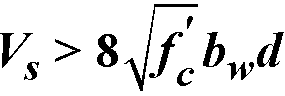 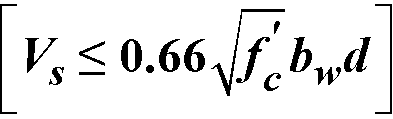 for ACI codes and 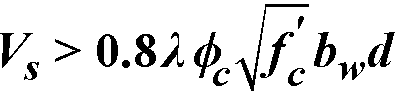for CSA A23.3-94 code, the beam section dimensions must be increased or a higher concrete strength must be provided¹⁰⁹.

The minimum shear reinforcement requirement is waived¹¹⁰ for joist construction and for beams satisfying the following criteria

For ACI 318-14, ACI 318-11 and ACI 318-08

•Beams with depth not exceeding 10 in. [250 mm].

•Beams integral with slabs (assumed by the program for all beams in two-way systems and beams within one-way slabs with overall width larger than effective beam flange width), with beam depth not exceeding 24 in. [600 mm] and not greater than the larger of 2.5 times flange thickness and 0.5 times web width.

For ACI 318-05/02/99

•Beams with depth not exceeding the largest of 10 in. [250 mm], 2.5 times flange thick­ness, and half of web width (rectangular beams are assumed by the program to have flange thickness equal to zero and web width equal to beam width).

For CSA A23.3-94

•Beams with depth not exceeding 250 mm.

•Beams integral with slabs (assumed by the program for all beams in two-way systems and beams within one-way slabs with overall width larger than effective beam flange width), with beam depth not exceeding the larger of 600 mm and 0.5 times web width.

2.12.2Shear Calculations for CSA A23.3-14/04

For CSA A23.3-04 code, the program calculates shear strength V_c provided by concrete from the following equation¹¹¹

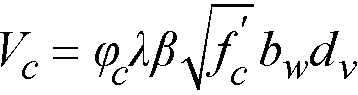      Eq. 2-59

where

f_c   =   resistance factor for concrete equal to 0.65 for regular and 0.70 for precast concrete

λ   =   factor to account for low-density concrete

b _w   =   beam web width

d _v   =   effective shear depth equal to greater of 0.9d or 0.72h

β   =   factor accounting for shear resistance of cracked concrete

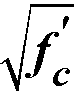   <   8 MPa.

When 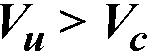, the beam must be provided with at least minimum shear reinforcement¹¹². Additionally minimum shear reinforcement is required for beam sections with overall thickness exceeding 750mm. Minimum area of shear reinforcement is calculated from the following formula¹¹³

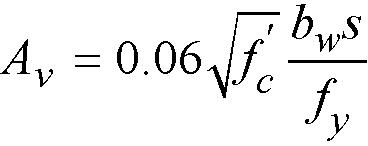      Eq. 2-60

Shear strength provided by shear reinforcement, V_s, is calculated from the following equation¹¹⁴

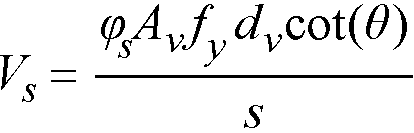      Eq. 2-61

where

f_s   =   resistance factor for reinforcement steel¹¹⁵ equal to 0.85

A_v   =   area of shear reinforcement within distance s

f _y   =   yield strength of reinforcement

d _v   =   effective shear depth equal greater of 0.9d or 0.72h

s   =   spacing of transverse reinforcement

θ   =   the angle of inclination of diagonal compressive stresses.

Spacing of transverse reinforcement, s, must not exceed the smaller¹¹⁶ of 0.7 d and 600 mm when 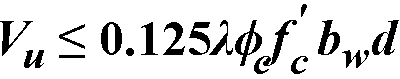or the smaller¹¹⁷ of 0.35 d and 300 mm when .

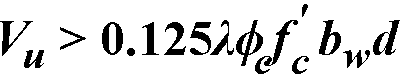When 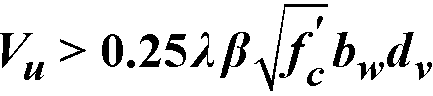, the beam section dimensions must be increased or a higher concrete strength must be provided¹¹⁸.

The program recognizes special member types and assumes values of β = 0.21 and θ = 42deg in the following cases¹¹⁹

•Slabs (including slab bands for CSA code) having thickness not exceeding 350 mm.

•Beams having thickness not exceeding 250 mm.

•Concrete joist construction.

•Beams cast monolithically with the slab and having the depth below the slab not exceed­ing one-half of the width or 350mm.

For other general cases the program utilizes the so called simplified method. The value of θ is assumed as 35deg. For sections having or requiring at least minimum transverse reinforcement β = 0.18 is assumed. For sections with no transverse reinforcement the value of β is calculated as follows¹²⁰

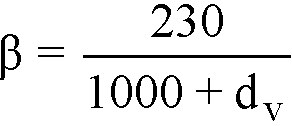      Eq. 2-62

2.12.3Shear Distribution

When no ribs are present, one way shear is proportioned to the slab and beam according to the following ratios

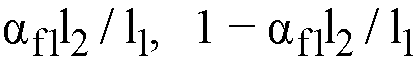      Eq. 2-63

When ribs are present (joist systems), one way shear is proportioned to the slab and beam according to the following ratios of cross-section areas

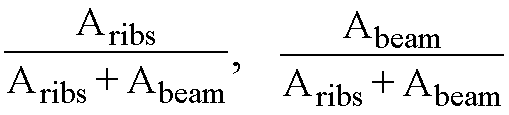      Eq. 2-64

Per requirement¹²¹ of CSA A23.3-14/04, the program allows distributing one-way shear in the slab between column and middle strips using the distribution factors which are proportional to the factors used for negative moment distribution. The fraction of the shear transferred to the beam remains unchanged irrespective of the use of this feature. This functionality is also provided for other design codes, to be selected at engineer’s discretion.

2.12.4One-Way Shear in Slab Bands (CSA A23.3-14/04)

One-way shear calculations in slab bands are done similar to shear in two-way slabs, except the column strip is substituted by the band strip. Shear forces are distributed between the band and the middle strip proportionally to negative moment distribution factors. Transverse reinforcement is not considered.

2.12.5Shear in Drop Panels

When calculating one-way shear capacity for two-way solid and waffle slabs, the contribution of the drop panel cross-section can be optionally selected. For such slabs, the shear capacity is calculated in three regions, with increased V_c values in support (drop panel) locations. In case shear is distributed into column and middle strips, drop panel contribution is divided according to the share of drop panel cross-section area in each strip.

2.13Torsion and Shear

Torsion analysis can be engaged for beam and one way systems using the Torsion Analysis and Design check box located on the Solve Options tab in the Input | General Information dialog box.

As far as torsional analysis is concerned, it is assumed that columns provide perfectly rigid supports so there is no transfer of torsional moments between spans. Within a span, torsional moments are considered only if a longitudinal beam is present. Torsion can be induced by concentrated and redistributed torsional loads and also, in the case of a beam with unsymmetrical cross sections, by self weight and area loads. A T-section with different flange widths is an example of a cross section which is not symmetrical. It can be obtained if a beam and a slab with different left and right widths are combined in the same span. However, in order for a flange to be considered in the torsional analysis its thickness has to be greater than twice the cover. If a flange is wider than the effective width then only the effective width is taken into account.

The design for torsion is based on a thin-walled tube, space truss analogy. For the Canadian code the simplified method is used. The program allows both equilibrium and compatibility torsion conditions. In the equilibrium mode, which is assumed by default, unreduced total value of the torsional design moment is used in the design. In the compatibility mode¹²², factored torsional moments that exceed cracking moment T_er (0.67 T_er for CSA) are reduced to the value of T_er (0.67 T_er for CSA). However, it is user’s responsibility to determine which mode is appropriate and the program does not perform any redistribution of internal forces if compatibility torsion is selected.

If torsion analysis is engaged then both torsion and shear actions contribute to the amount of required transverse (stirrup) reinforcement. However, additional longitudinal bars distributed along the perimeter of a cross-section are also required to provide torsional capacity.

For torsion design a span is divided into segments in the same way as for shear design. Governing values within a segment are used to design the whole segment. For stirrups, the governing values of torsional moment and shear force (acting simultaneously) will be these that produce the highest intensity of required stirrup area. On the other hand, the required area of longitudinal bars depends only on the torsional moment so the highest absolute value of torsional moment will govern. Since stirrup area depends both on shear and torsion whereas longitudinal bar area depends only on torsion, the governing values for stirrups and longitudinal bars can occur at different locations within a segment and for different load combinations. Governing values along with their location and associated load combination are provided in the design results report.

Effect of torsion within a segment will be neglected if the factored torsional moment, T_u, at every segment location is less than one fourth of the torsion cracking moment, T_er, which equals

for ACI code¹²³

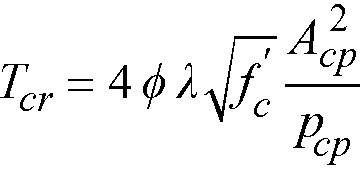      Eq. 2-65

for CSA A23.3-94 code¹²⁴ 

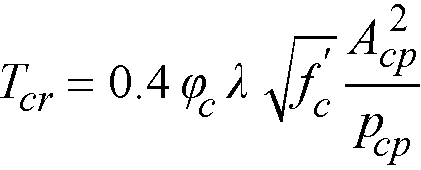      Eq. 2-66

for CSA A23.3-14/04 code¹²⁵

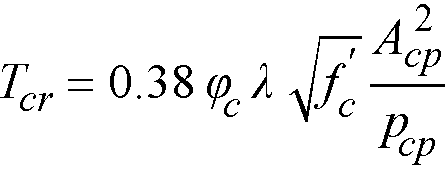      Eq. 2-67

A_cp denotes the area enclosed by outside perimeter of concrete section and p_cp is equal to the outside perimeter of concrete section.

To be adequate for torsion design, a section has to be proportioned in such a way that combined shear stress due to shear and torsion does not exceed the limit value specified by the code. In ACI code this condition reads as¹²⁶

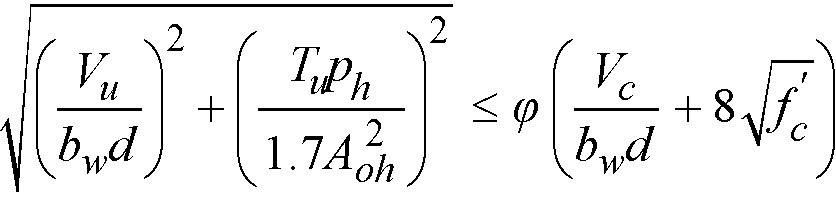      Eq. 2-68

The simplified method of CSA A23.3-94 standard defines this relation as¹²⁷

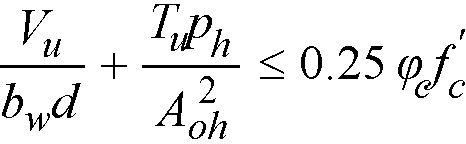      Eq. 2-69

Similar requirement for CSA A23.3-04 reads as follows¹²⁸

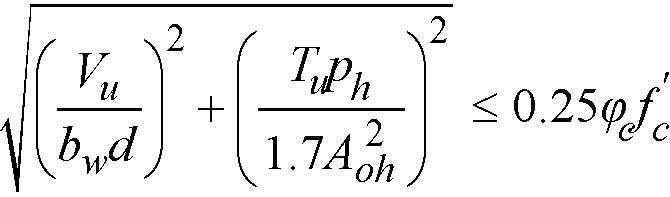      Eq. 2-70

In above relations, A_oh is the area enclosed by centerline of the outermost closed transverse reinforcement and p_h is the perimeter of that area. By default, flanges do not contribute to A_oh and p_h. For sections with flanges, flanges will only be taken into account for A_oh and p_h if the option to include stirrups in flanges is engaged in the torsion design. In the program output, the combined stress (left hand side of the above inequalities) is denoted as v_f and the limit value as ϕs_vt.

The required intensity of stirrup area to provide required torsional capacity is calculated from the following formula¹²⁹

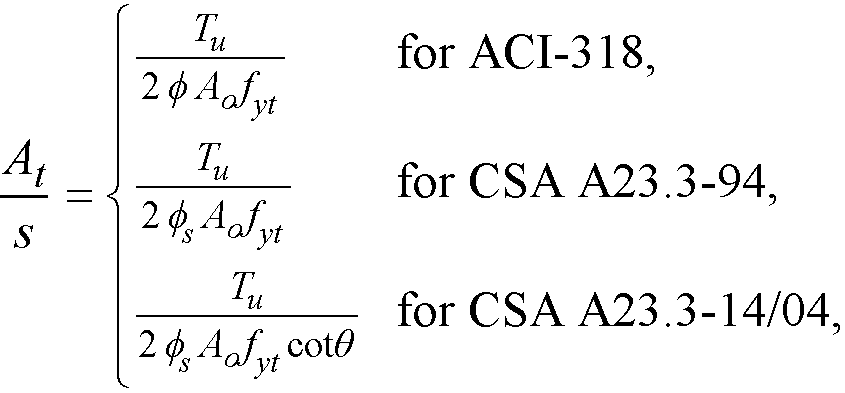      Eq. 2-71

where the gross area enclosed by the shear path¹³⁰, A_o, is taken as 0.85A_oh. A_t /s is the quantity per stirrup leg. Concrete shear and torsion strength reduction factor¹³¹, f, for ACI-318 codes is equal to 0.75 for the 99 edition and 0.75 for later editions.

The total requirement for stirrup intensity combining shear and torsion equals¹³²

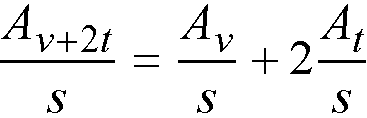      Eq. 2-72

This value cannot be taken less than minimum stirrup area required by the codes. The minimum code requirements can be written in the following form¹³³

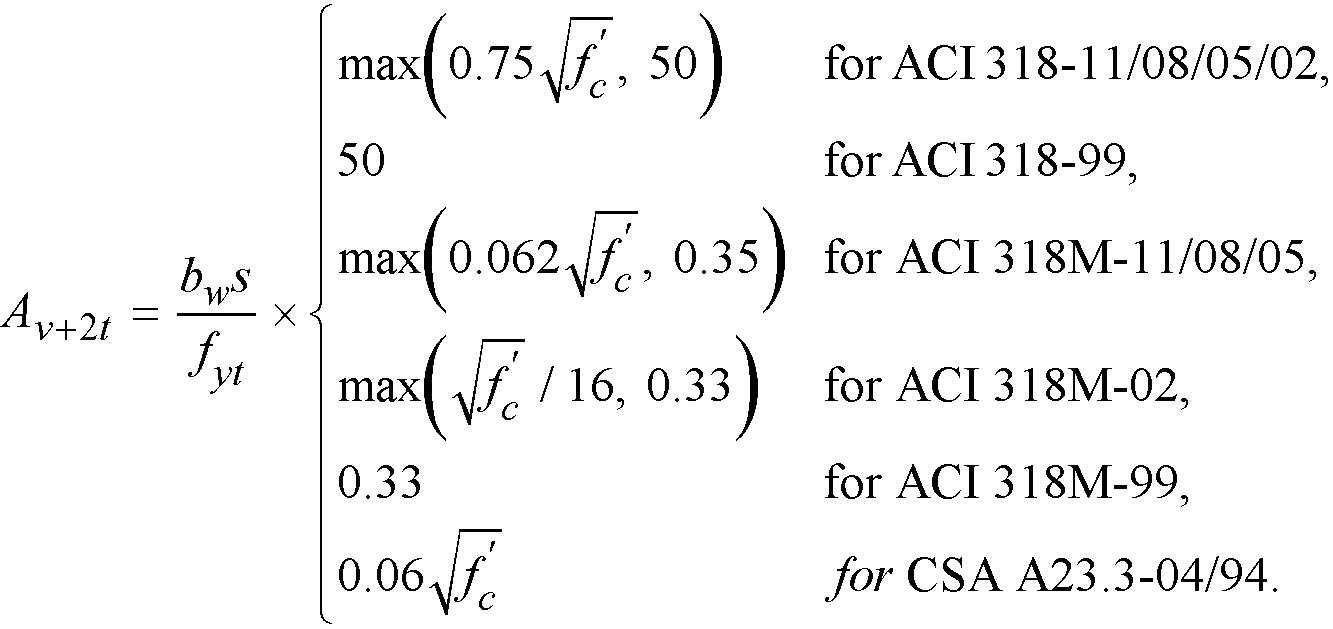      Eq. 2-73

In addition to stirrup spacing requirement defined for shear, program imposes one more torsion specific requirement for all ACI codes¹³⁴ which limits the spacing to the smallest of 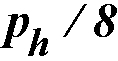, and 12 in [300 mm]. Based on the total required stirrup area intensity and spacing requirements, the program attempts to select stirrups taking also into account that if stirrups with more than two legs have to be used then the area of an outer leg must not be less than A_t.

2.13.1Additional Longitudinal Reinforcement for ACI 318 and CSA A23.3-94

The area of additional longitudinal reinforcement, A_ℓ, is calculated from¹³⁵

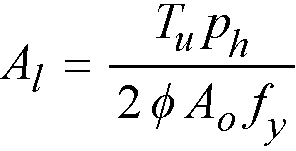      Eq. 2-74

For ACI code it is also checked against the following minimum value¹³⁶

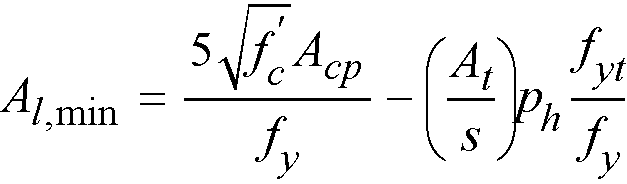      Eq. 2-75

where A_t / s is calculated from Eq. 2-56 but is not taken less than 25b_w / f_yt. Longitudinal bars are selected in such a way that their area is not less than A_ℓ > A_ℓ,min and that number of longitudinal bars in a section is enough to provide a bar in every corner of a stirrup and preserve spacing between bars not higher than 12 in [300 mm]. Also, bar sizes are selected not to have diameter less than No. 3 bar and not less than 1/24 of stirrup spacing for ACI codes¹³⁷ and 1/16 for CSA standard¹³⁸.

2.13.2Additional Longitudinal Reinforcement for CSA A23.3-14/04

The additional longitudinal reinforcement, A_ℓ, will only be calculated for CSA A23.3-14/04 if option Combined M-V-T Reinf. Design is unchecked in the Solve Options dialog window. If this option is checked (default setting) then no additional longitudinal reinforcement is calculated because the regular top and bottom reinforcement will automatically be proportioned to resist combined action of flexure, shear and torsion.

Proportioning of longitudinal reinforcement for sections subjected to combined shear and torsion in flexural regions is based on the requirement that the resistance of the longitudinal reinforcement has to be greater or equal to the axial force that can be developed in this reinforcement. In sections with no axial action (N_f = 0 and V_p = 0) that force is equal to¹³⁹

•flexural tension side

 

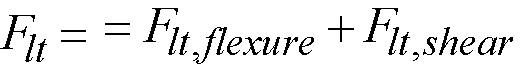
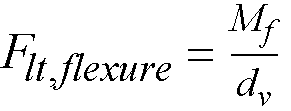 and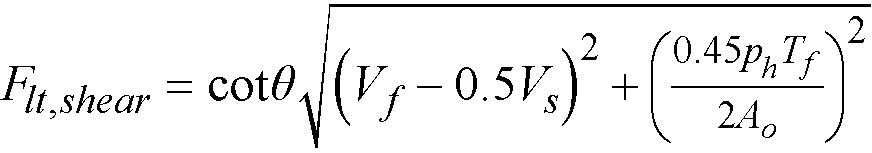

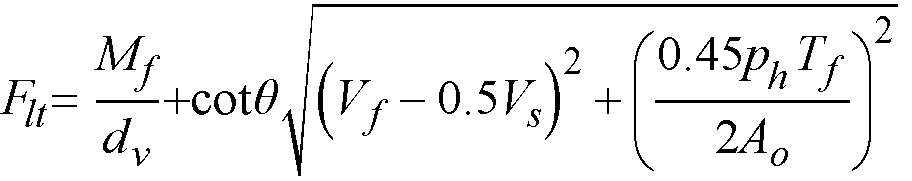      Eq. 2-76

•flexural compression side

 

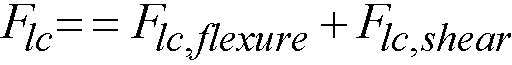
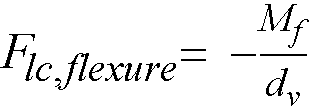 and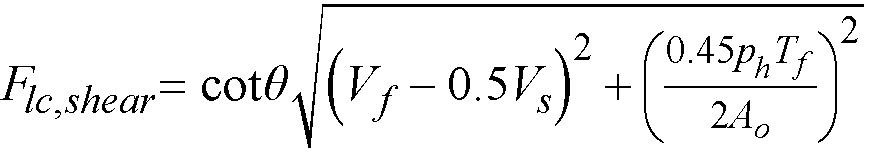

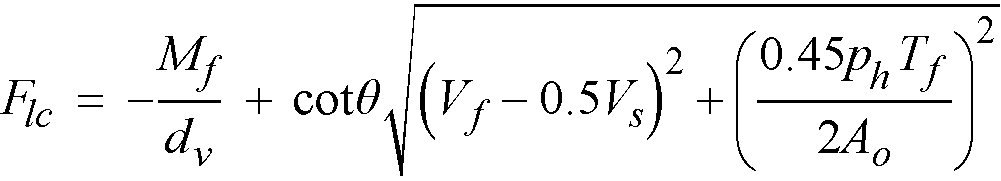      Eq. 2-77

These forces can be decomposed¹⁴⁰ into flexure and shear components. The flexure components, F_lt,flexure and F_lc,flexure, account for the action of the bending moment, M_f, whereas the shear components, F_lt,shear and F_lc,shear, account for the action of the shear force, V_f, and the torsional moment, T_f. The amounts of reinforcement needed to resist the flexure components are calculated separately in the flexure design procedure. The total amount of the additional longitudinal reinforcement, A_ℓ, needed to resist shear and torsion will be determined as follows

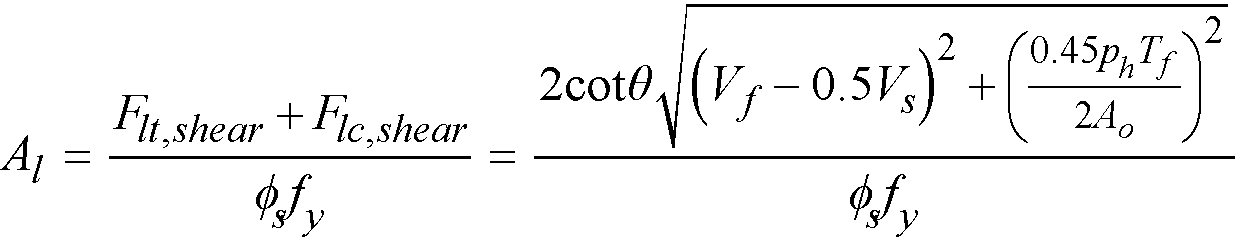      Eq. 2-78

If only torsion is present (V_f = 0 and V_s = 0), then (assuming¹⁴¹ θ = 35°) A_ℓ would reduce to

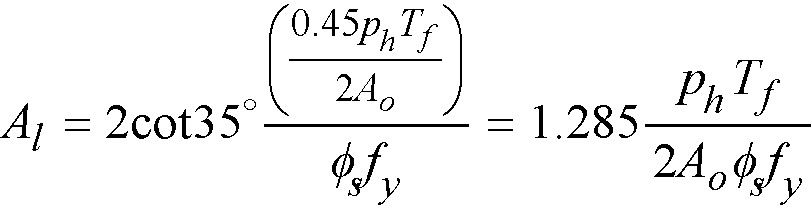      Eq. 2-79

which is comparable (and conservative) to the additional amount of longitudinal reinforcement due to torsion required in accordance with the previous edition of the CSA A23.3 standard¹⁴².

2.13.3Investigation Mode

In the investigation mode when transverse and longitudinal reinforcement is input by the user, the program checks the combined shear and torsional capacity of the system in terms of required and provided reinforcement area. In other words, the provided area of reinforcement is compared to the area of reinforcement required to resist applied loads. This is a different approach than for flexure and shear actions without coupling where design forces are directly compared to capacity. In the case where torsion and shear stirrup requirements are combined, the approach of comparing total reinforcement area is more convenient since it does not require dividing stirrup area into a part that resists torsion only and a part that resists shear only. For consistency, additional longitudinal reinforcement required for torsion and shear is also checked in terms of provided and required area. Other requirements, e.g. bar or stirrup spacing, number of longitudinal bars, area of stirrup outer leg, and combined stresses in concrete due to shear and torsion are checked also. Exceeded capacity and other conditions are flagged in the Design Results section of the report.

2.14Area of Reinforcement

The program calculates the required area of reinforcement (top and bottom) based on the values of bending moment envelope within the clear span. For rectangular sections with no compression reinforcement, the design flexural strength of the column strip, middle strip and beam must equal the factored design moment

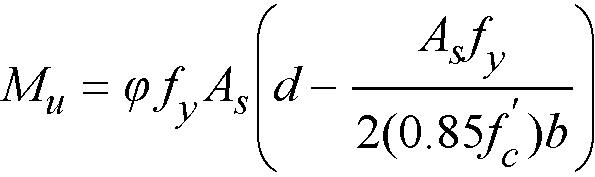      Eq. 2-80

The reinforcement can therefore be computed from

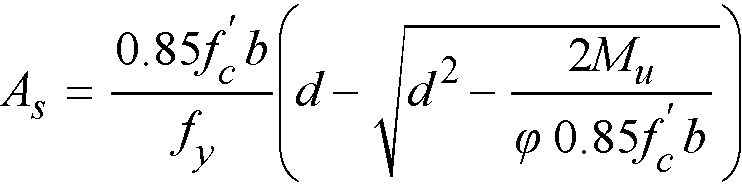      Eq. 2-81

For CSA A23.3

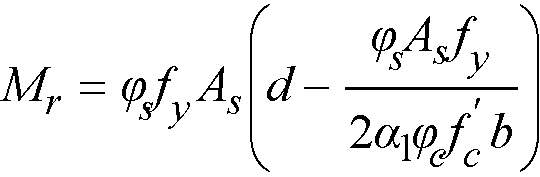      Eq. 2-82

The effective depth of the section is taken as the overall section depth minus the distance from the extreme tension fiber to the tension reinforcement centroid. The column strip depth may include all or part of the drop panel depth. The drop depth will not be included in the effective depth of the column strip when the drop does not extend at least one-sixth the center-to-center span length in all directions, or when the drop depth below the slab is less than one-quarter the slab depth. If the drop extends at least one-sixth the center-to-center span length and the drop depth is greater than one-quarter the distance from the edge of the drop panel to the face of the column or column capital, the excess depth will not be included in the column strip effective depth. If the drop width is less than the column strip width, the drop width will be used in the computation of the required reinforcement.

When computing negative slab reinforcement and additional reinforcement for negative unbalanced moments over the supports, the contribution of the depth of transverse beam can be optionally selected. The contribution of transverse beam will be considered, if it extends beyond the critical section and if its depth exceeds the depth of the drop panel. The increase of the slab thickness is limited to ¼ of the extent of the transverse beam beyond the face of support, identical to design depth limitations for drop panels. If transverse beam depth exceeds the limit, excess depth is disregarded in the reinforcement calculations.

For two-way slabs with beams, an option exists when designing reinforcement for positive bending moments, to include a portion of slab as beam flanges¹⁴³

 (T-Section). The width of the column strip is then decreased accordingly. The extent of the flanges on each side is limited to four times slab thickness and not more that the projection of the beam under the slab. When this option is not selected, beam geometry is treated as rectangular. When calculating required reinforcement for negative bending moments the geometry of the beam is treated as rectangular, having beam width equal to web width. However, when a T-Section is selected, reinforcing bar design is performed assuming that they are distributed across the beam width including the flanges.

For the ACI 318-99 code the strength reduction factor for flexure calculations is specified as f=0.90.¹⁴⁴ For the ACI 318-14, ACI 318-11, ACI 318-08, ACI 318-05, and ACI 318-02 codes the strength reduction factor for tension-controlled sections (εt > 0.005) is equal f=0.90. For transition sections (f_y / E_s < ε_t < 0.005) the strength reduction factor can be linearly interpolated by the formula¹⁴⁵

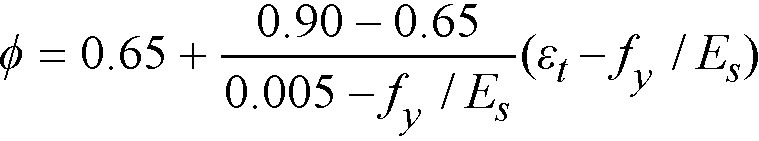      Eq. 2-83

ACI 318-14, ACI 318-11, ACI 318-08, ACI 318-05, and ACI 318-02 codes specify the strength reduction factor for compression controlled sections (e_t < f_y E_s) as equal f=0.65. The reduction factors for transition or compression controlled sections have application primarily in investigation mode of the program. In design mode the program performs the calculations assuming a tension controlled section (e_t ≥ 0.005) or a section with compressive reinforcement (if enabled).

The ACI 318-99 code¹⁴⁶ requires keeping the steel ratio below the maximum value, r_max, equal to 75% of steel ratio producing balanced strain condition, r_b, where¹⁴⁷

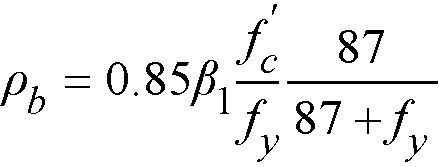      Eq. 2-84

with

β₁    =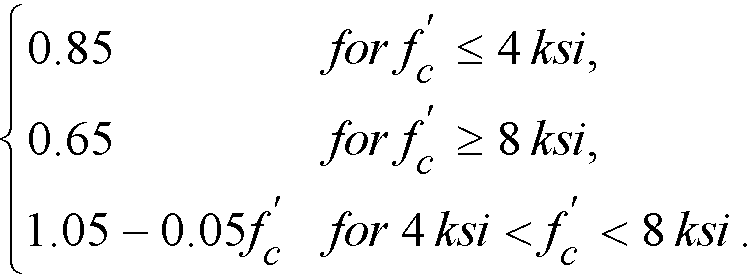   

For CSA code the value of r_max equals r_b and is calculated as follows¹⁴⁸

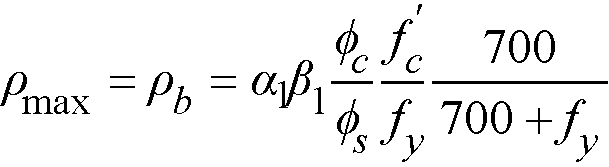      Eq. 2-85

where

a₁   =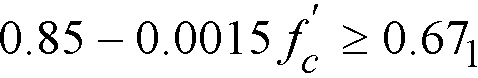   

β₁    =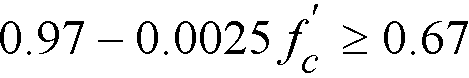   

The ACI 318-14, ACI 318-11, ACI 318-08, ACI 318-05, and ACI 318-02 codes control the amount of reinforcement by limiting the value of net tensile strain (e_t ≥ 0.004)¹⁴⁹. The program satisfies this condition by assuming a tensioned controlled section with e_t ≥ 0.005. From this assumption the equivalent maximum reinforcement ratio for rectangular section can be written as

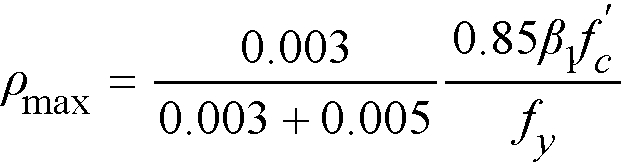      Eq. 2-86

If the calculated reinforcement exceeds the maximum allowed, a message will appear in the output. In such cases, it is recommended that the engineer review the slab thickness to ensure a more satisfactory design. If compression reinforcement calculations are enabled, the program will attempt to add compression reinforcement to the section. The program is capable to design compressive reinforcement for any design strip (column, middle, and beam) including also unbalanced moment strip¹⁵⁰.

The amount of reinforcement provided will not be less than the code prescribed minimum. For the ACI 318 code, the minimum ratio of reinforcement area to the gross sectional area of the slab strip using Grade 60 reinforcement is taken as 0.0018. When reinforcement yield strength exceeds 60 ksi, the minimum ratio is set to 0.0015×60 / f_y. For reinforcement with yield strength less than 60 ksi, the minimum ratio is set to 0.0020. In no case will this ratio be less than 0.0014 (See Table 2-5)¹⁵¹. The CSA Standard requires a minimum ratio of slab reinforcement area to gross sectional area of the slab strip equal to 0.002 for all grades of reinforcement¹⁵².

Table 2.4 Minimum Ratios of Reinforcement to Gross Concrete Area

According to ACI code for beams and positive moment regions of joist slabs, minimum reinforcement provided will not be less than¹⁵³

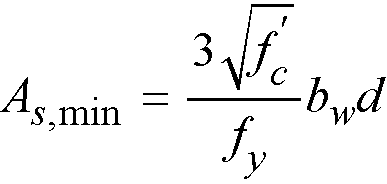      Eq. 2-87

and not less than 200b_wd/f_y where b_w is the web width of the section. For statically determinate sections with flange in tension, b_w is replaced by the smaller of 2b_w and the width of the flange.

Similar equation prescribed by CSA A23.3 code has the form¹⁵⁴

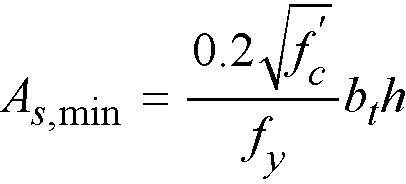      Eq. 2-88

where b_t is the width of the tension zone of the section. Additionally, for T-sections having flange in tension the CSA code limits value of b_t to 1.5b_w for single sided flanges and to 2.5b_w for double sided flanges.

When designing reinforcement for longitudinal slab bands according to CSA code, program assumes identical minimum steel requirements as for beams.

2.14.1Design for Combined Flexure, Shear, and Torsion

CSA A23.3-14/04 requires, in proportioning of longitudinal reinforcement, to include additional tension forces caused by shear and torsion¹⁵⁵. To achieve this, the program calculates forces developed in the longitudinal reinforcement due to flexure, shear, and torsion.

On the flexural tension side the force in longitudinal reinforcement is equal to¹⁵⁶

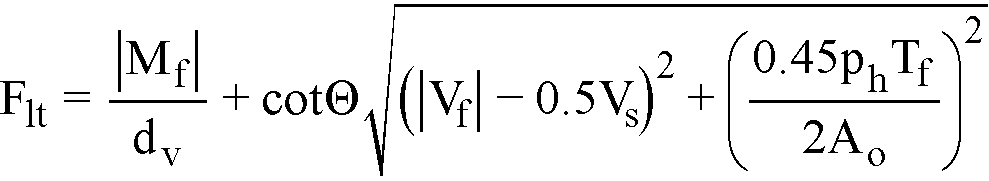      Eq. 2-89

On the flexural compression side the force in longitudinal reinforcement is equal to¹⁵⁷

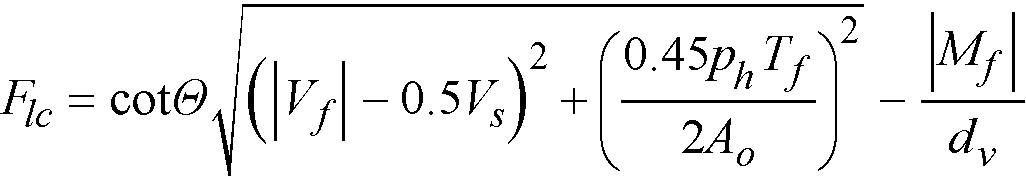      Eq. 2-90

but not less than zero.

For these forces, longitudinal reinforcement area is calculated from the following equations¹⁵⁸

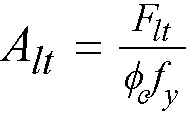      Eq. 2-91

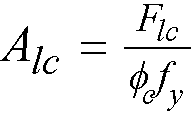      Eq. 2-92

Taking into account both positive and negative bending moments (resulting from all load combinations and load patterns) and checking against area of steel required for flexure only, the final areas of top and bottom reinforcement can be calculated from

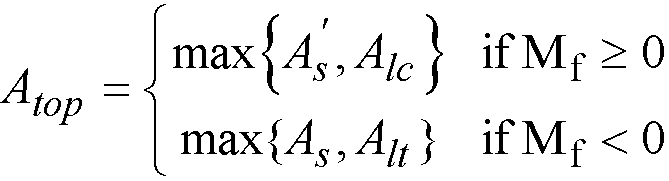      Eq. 2-93

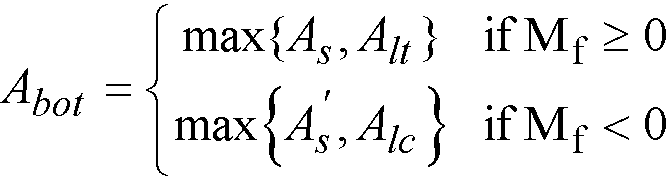      Eq. 2-94

2.15Reinforcement Selection

According to ACI-318 code¹⁵⁹, the default minimum clear spacing of reinforcement for both slabs and beams is taken as the larger of the two prescribed minima of one bar diameter, d_b, or 1 in. According to CSA code¹⁶⁰, the default minimum clear spacing of reinforcement for both slabs and beams is taken as the larger of the two prescribed minima of 1.4 times the bar diameter, d_b, or 1.2 in (30mm). The user may select a clear spacing greater than the default value to take into account tolerances for reinforcement placement¹⁶¹ and other project specific considerations.

For two-way systems, the maximum spacing of reinforcement is kept at two times the slab thickness for the ACI code¹⁶² and three times the slab thickness for the CSA code¹⁶³, but no more than 18 in. or 500 mm respectively. For joist systems the limit is increased to 5 times the slab thickness¹⁶⁴. When calculating negative support reinforcement for the CSA code¹⁶⁵, the program assumes that banded reinforcement over supports is spaced at a maximum of 1.5 h_s and no more than 250 mm.

For one-way slabs, the maximum spacing is limited to¹⁶⁶ the smaller of three times the slab thickness and 18 in. [500 mm]. Additionally, the maximum spacing of reinforcement, s, in beams and one-way slabs is selected so that the following crack control requirements of the ACI and the CSA codes¹⁶⁷ are met

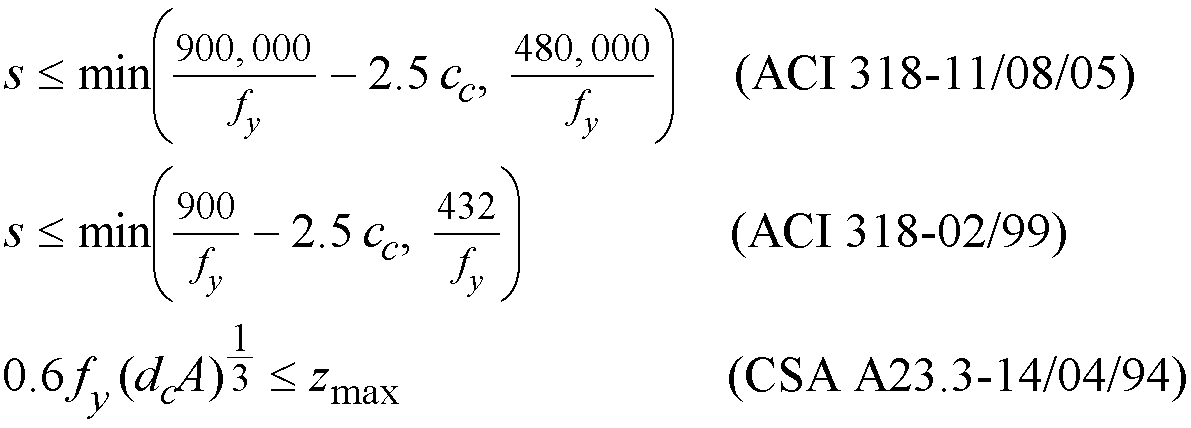      Eq. 2-95

where

c_c    =   least distance from the surface of bar to the tension face,

d_c    =   distance from extreme tension fiber to center of the closest longitudinal bar

A   =    effective tension area of concrete surrounding the flexural tension reinforcement and extending from the extreme tension fiber to the centroid of the flexural tension reinforcement and an equal distance past that centroid, divided by the number of bars or wires

z_max   =    30 000 N/mm for interior exposure or 25 000 N/mm for exterior exposure, multiplied by a factor of 1.2 for epoxy-coated reinforcement

An iterative process is performed to determine the number of bars and bar size. The initial number of bars is determined by dividing the total reinforcement area required, A_s, by the area of one bar, A_sb, of the input minimum bar size. Next, the spacing is determined. If the minimum spacing limitations are violated, the bar size is increased and the iterative process is repeated until all bars sizes have been checked. If the maximum spacing limitations are not met, the number of bars required to satisfy these limitations is computed and the iteration process terminates.

 

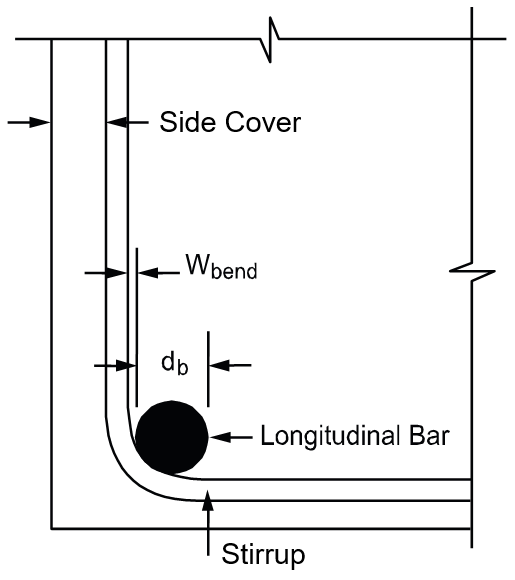
Figure 2.21 Width due to stirrup bend

For beams, layered reinforcement is provided if sufficient beam width is not available. The clear distance between layers is assumed 1.0 in [30 mm] but the user can change this value. By default, the program assumes a 1.5 in [40 mm] side cover to stirrup for width calculations and this value can also be changed by the user. The program also assumes that the longitudinal bar makes contact at the middle of the stirrup bend where the minimum inside diameter of the bend is four times stirrup diameter¹⁶⁸. Therefore, an additional width is added to the cover for longitudinal bars less than size #14 (#45 for CAN/CSA-G30.18) (Figure 2-21). This additional width due to the bend, w_bend, is equal to

      Eq. 2-96

where

d_b    =    diameter of the longitudinal bar

r    =    inside radius of bend for stirrup

 

Figure 2.22 Detail reinforcement in longitudinal beams

Bar-length computations are performed for two-way slabs and longitudinal beams. For top reinforcement at the supports, the length for long bars is given by

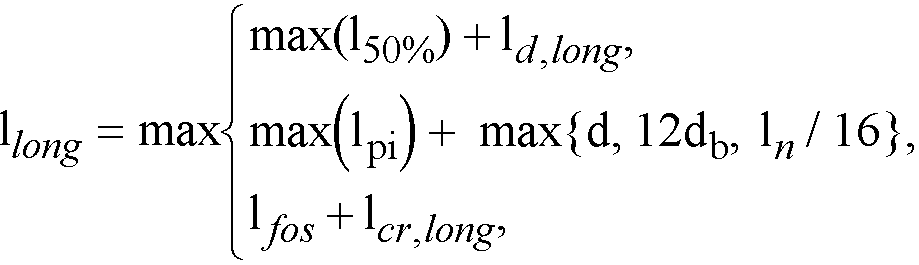      Eq. 2-97

and the length for short bars is given by

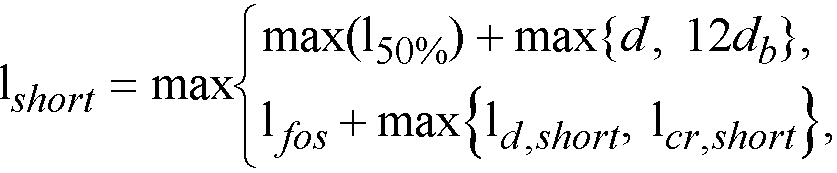      Eq. 2-98

where

max(l_50%)   =   maximum distance to the points of 50% demand,

max(l_pi)   =   maximum distance to the points of inflection (P.I.),

l_d   =   bar development length¹⁶⁹,

d   =   effective depth,

d_b   =   bar diameter,

l_n   =   clear span length,

l_fos   =   distance to the face of support (column),

l_cr   =   minimum code prescribed extension.

These bar lengths are then compared and adjusted if necessary to meet the minimum extension requirements for reinforcement specified by the code.¹⁷⁰ Additionally the program may select continuous top bars in those spans where steel is required by calculation in mid-span at top.

If the computed bar lengths overlap, it is recommended that such reinforcement be run continuously. The printed bar lengths do not include hooks or portions of bars bent down into spandrel beams or other bar-bend configurations. If a bar starts (or ends) at a column support the length of the bar is measured from (or to) the center line of the column. The selection of bar lengths for positive reinforcement for flat plates, flat slabs, and beam-supported slabs, is based strictly on the minimum values of the code.

The development length depends on the following factors: concrete cover, minimum transverse reinforcement, special transverse reinforcement, layer location bar size and bar clear spacing. The development length is calculated from the general expression¹⁷¹ below, but not less ¹⁷² than 12 in [300 mm]

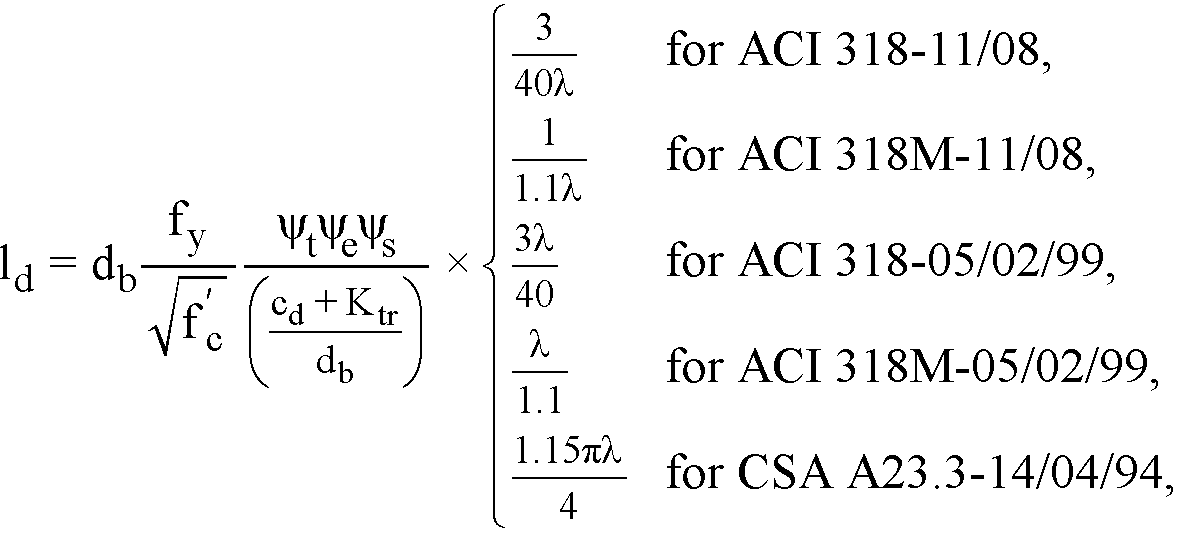      Eq. 2-99

where

y_t   =   reinforcement location factor equal to 1.3 if more than 12 in [300 mm] of fresh concrete is cast in the member below the development length or splice, or equal to 1.0 otherwise,

y_e   =   coating factor equal to 1.0 for uncoated reinforcement; for epoxy coated reinforcement with covers less than 3d_b or clear spacing less than 6d_b the factor is equal to 1.5 and for all other epoxy coated bars it equals 1.2,

y_s   =   reinforcement size factor equal to 1.0 for bars #7 [22] and larger or equal to 0.8 for bars #6 [19] and smaller if ACI 318 [ACI 318M] is selected; for CSA A23.3 the factor is equal to 1.0 for bars 25M and larger or equal to 0.8 for bars 20M and smaller,

λ   =   lightweight aggregate concrete factor equal to 1.0 for normal concrete and:

      0.75 for lightweight concrete per ACI 318-14, ACI 318-11 and ACI 318-08

      1.3 for lightweight concrete per ACI 318-05/02/99

      1.3 for low density concrete per CSA A23.3-14/04/94

      1.2 for semi low density concrete per CSA A23.3-14/04/94

K_tr   =   transverse reinforcement index conservatively assumed zero,

c_b   =   smaller of the distance form bar surface to the closest concrete surface and one-half (two thirds for CSA¹⁷³) center-to-center bar spacing.¹⁷⁴

Additionally, the product of y_ty_e is not taken greater than 1.7 and the development length, l_d, is reduced¹⁷⁵ by the factor of A_s,req to A_s,prov where the provided area of flexural reinforcement, A_s,prov, exceeds the area required by analysis, A_s,req.

The final calculated or minimum development length for each bar is tabulated in the design results section of the program results report. In two-way slab systems without beams, the development length presented is often controlled by the minimum development length.

Where flexural reinforcement is terminated in a tension zone, spSlab and spBeam provide a warning to require an extension of the bar beyond what is required for flexure. For ACI code, the shear capacity at the cutoff point for each bar is evaluated for satisfying the shear demand does not exceed permissible shear limit in 12.10.5.1.  Final bar length shall be extended beyond the minimum reported to meet one of the three conditions outlined in 12.10.5

2.16Concentration and Additional Reinforcement

spSlab computes the fraction of the unbalanced moment, g_f M_u, that must be transferred by flexure within an effective slab width (a band) equal to the column width plus one and one-half the slab or drop panel depth (1.5h) on either side of the column where¹⁷⁶

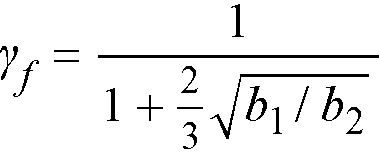      Eq. 2-100

The amount of reinforcement required to resist this moment is computed. The amount of reinforcement already provided for flexure is then computed from the bar schedule (i.e. the number of bars that fall within the effective slab width multiplied by the area of each bar). Depending on load conditions, additional negative or positive reinforcement may be required. If the reinforcement area provided for flexure is greater than or equal to the reinforcement requirements to resist moment transfer by flexure, no additional reinforcement is provided, and the number of additional bars will be set to 0. If the amount of reinforcement provided for flexure is less than that required for moment transfer by flexure, additional reinforcement is required. The additional reinforcement is the difference between that required for unbalanced moment transfer by flexure and that provided for design bending moment in the slab, and it is selected based on the bar size already provided at the support.

For ACI codes the value of g_f on selected supports can be automatically adjusted to the maximum permitted value. The corresponding value of g_v = 1 – g_f is adjusted accordingly. This option allows relaxing stress levels for two-way shear around the columns by transferring increased part of the unbalanced moment through flexure. The adjustment is performed independently for each load case and pattern. If for given load case the corresponding two-way shear V_u exceeds the appropriate limits 0.75fV_c at an edge support, 0.5fV_c at a corner support, or 0.4fV_c at an interior support, adjustment of both factors is not performed. When the adjustment of g_f and g_v factors is selected, the reinforcement calculated within the transfer width should be limited according to the code to reinforcement ratio r < 0 .375r_b, as stipulated in ACI 318-99/02/05¹⁷⁷, or limitation of net tensile strain e_t > 0.010, as required by ACI 318-14, ACI 318-11 and ACI 318-08¹⁷⁸. Violation of this requirement is reported by the software as exceeding maximum allowable reinforcement indicating that the option to adjust the factor g_f should be turned off by the user at the support where the violation occurs.

It should be noted that the ACI code¹⁷⁹ requires either concentration of reinforcement over the column by closer spacing, or additional reinforcement, to resist the transfer moment within the effective slab width. spSlab satisfies this requirement by providing additional reinforcement without concentrating existing reinforcement.

When computing additional reinforcement for the transfer of negative and positive unbalanced moments over the supports through flexure in systems with longitudinal beams, the contribution of the longitudinal beam cross-section can be optionally selected. If selected, this contribution will be considered. For CSA designs this functionality extends also to design of banded reinforcement in b_b strip.

The CSA A23.3 code requires at least one-third of the total negative reinforcement for the entire design strip at interior supports to be concentrated in the band width, b_b, extending 1.5 h_s from the sides of the columns¹⁸⁰. The program fulfills this requirement by concentrating a portion of reinforcement assigned to the design strip that includes width b_b. This strip will typically be the column strip. However, if longitudinal slab bands or slab-band-like beams wider than band width b_b are present, then reinforcement assigned to these elements is concentrated. At exterior supports, the total negative reinforcement is placed in the b_b band width¹⁸¹ or if a beam narrower than b_b is present, then the total reinforcement is placed within the beam width¹⁸². The reinforcement in the b_b and the remaining portions of the design strip is also checked for compliance with spacing and minimum reinforcement requirements.

2.17Structural Integrity Reinforcement

Enhancing redundancy and ductility is necessary in the event of damage to a major supporting element resulting from an abnormal shock or blast loading event.

Minor changes in reinforcement detailing typically result in substantial enhancement in the overall integrity of a structure by confining the resulting damage to a small area and improving the resistance to progressive collapse.

The ACI code requires all bottom bars in the column strip to extend continuously (or with splices) in the entire span and at least two of these bars to pass within the column core and to be anchored at exterior supports¹⁸³. In continuous beams, including longitudinal beams in two-way slab systems, spSlab and spBeam produce, in design mode, reinforcement that satisfies ACI requirements for structural integrity. In perimeter (exterior) beams, at least one sixth of the negative tension reinforcement and not less that two bars are continuous¹⁸⁴. Also, at least one fourth of the positive tension reinforcement and not less than two bars are continuous in all beams¹⁸⁵.

For the CSA code, the program performs calculation of the amount of integrity reinforcement at slab column connections in design mode. The integrity reinforcement is required for slabs without beams. Integrity reinforcement is not required if there are beams containing shear reinforcement in all spans framing into the column. Otherwise, the sum of all bottom reinforcement connecting the slab to the column on all faces of the periphery should consist of at least two bars and meet the condition¹⁸⁶

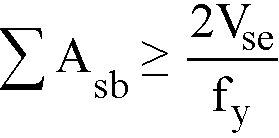      Eq. 2-101

where V_se is the larger of shear force transmitted to column or column capital due to specified (unfactored) loads and shear force corresponding to twice the self-weight of the slab.

2.18Corner Reinforcement

The program performs calculation of the amount of reinforcement in exterior corners of slabs with stiff edge beams (a greater than 1.0)¹⁸⁷. This reinforcement is required within a region equal to 1/5 of the shorter span. The amount of corner reinforcement is calculated from the moment per unit width intensity corresponding to the maximum positive moment in span. The code allows the corner reinforcement to be placed at top and bottom of the slab in bands parallel to the sides of the slab edges.

2.19Deflections

2.19.1Instantaneous Deflections

Instantaneous deflections are obtained directly by the program from elastic analysis of the defined system for three load levels. The first corresponds to dead load only, the second corresponds to dead load plus sustained part of live load only, and the third corresponds to dead load plus live load on all spans (total deflection). The deflection occurring when the live load is applied can be computed as the total load deflection (due to the dead and the live load ) minus the dead load only deflection¹⁸⁸. Depending on the option selected by the user, the program will calculate flexural stiffness of the members based on either gross moment of inertia or the effective moment of inertia which takes cracking into account.

 

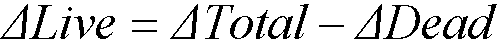
The program results section provides detailed summary of the frame section properties, frame effective section properties, column and middle strip properties at midpsan, and a summary of extreme deflection values for each load level along the span.

2.19.2Cracking

When calculating the deflections for effective (cracked) section properties, the frame solution is obtained for three load levels: dead load, dead load plus sustained part of live load, and dead load plus full live load on all spans. Flexural stiffness is assumed corresponding to the load level.

A reduction in the flexural stiffness caused by cracking leads to an increase in deflections. Several methods of deflection analyses taking cracking into account are reviewed in Ref. [22]. The program uses the approach based on the effective moment of inertia as permitted by the code.¹⁸⁹

The effective moment of inertia, I_e, developed by Branson (Ref. [17]) and incorporated into the code equals

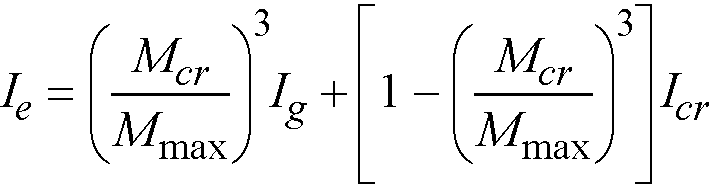      Eq. 2-102

where

I_g    =    moment of inertia of the gross uncracked concrete section,

I_cr    =    moment of inertia of the cracked transformed concrete section¹⁹⁰

M_cr    =    cracking moment

M_max    =    maximum bending moment at the load level for which the deflection is computed.

To calculate I_e for two-way slabs, the values of all terms for the full width of the equivalent frame are used in Eq. 2-102. This approach averages the effects of cracking in the column and middle strips.

The value of I_e at midspan for a simple span and at support for a cantilever is taken¹⁹¹ to calculate flexural stiffness of a member. For other conditions, an averaged effective moment of inertia, I_e,avg is used. For spans with both ends continuous, I_frame is given by¹⁹²

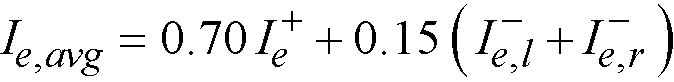      Eq. 2-103

where

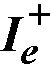    =    effective moment of inertia for the positive moment region,

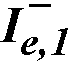    =    effective moment of inertia for the negative moment region at the left support,

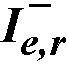    =    effective moment of inertia for the negative moment region at the right support.

For spans with one end continuous the value of I_frame is given by¹⁹³

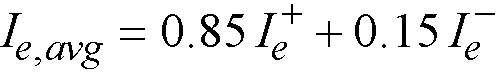      Eq. 2-104

where

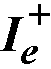    =    effective moment of inertia for the positive moment region,

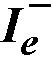    =    effective moment of inertia for the negative moment region at the continuous end.

2.19.3Long-Term Deflections

The program estimates additional long-term deflection resulting from creep and shrinkage, D_cs, by multiplying the immediate deflection due to sustained load, D_sust, by the factor, l_D, equal to¹⁹⁴

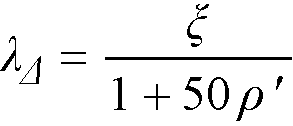      Eq. 2-105

where

x    =    time dependent factor with the maximum value of 2.0 (the actual value is interpolated from the values and the chart given in the code¹⁹⁵ based on the load duration specified by the user in the input)

r’   =    ratio of compressive reinforcement at midspan for simple and continuous spans and at support for cantilevers.

Deflection due to the sustained load, D_sust, is the deflection induced by the dead load (including self weight), plus sustained portion of the live load.

And long-term deflection resulting from creep and shrinkage equals

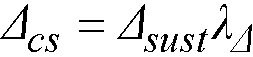      Eq. 2-106

The program calculates incremental deflection which occurs after partitions are installed in two ways. In the first approach, it is assumed that the live load has been applied before installing the partitions and the incremental deflection equals¹⁹⁶

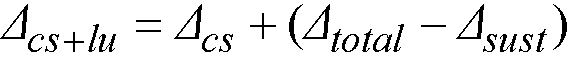      Eq. 2-107

In the second approach, the assumption is that the full live load, including the sustained portion of the live load, has been applied after the partitions are installed which results in the incremental deflection equal to¹⁹⁷

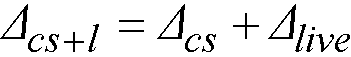      Eq. 2-108

The total long-term deflection (D_total)_lt is also calculated as¹⁹⁸

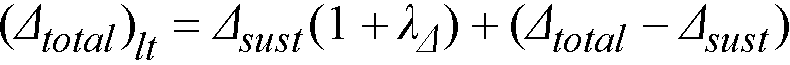      Eq. 2-109

2.19.4Deflections of two-way systems

Calculation of deflections of reinforced concrete two-way slabs is complicated by a large number of significant parameters such as: the aspect ratio of the panels, the vertical and torsional deflection of supporting beams, the stiffening effect of drop panels and column capitals, cracking, and the time-dependent nature of the material response. Based on studies (Ref. [20]-[22]), an approximate method consistent with the equivalent frame method was developed (Ref. [23]) to estimate the column and middle strip deflections.

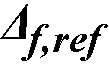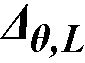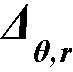Under vertical loads, Reference 20 indicates that the midspan deflection of an equivalent frame can be considered as the sum of three parts: that of the panel assumed to be fixed at both ends of its span,  and those due to the known rotation at the two support lines,  and . Calculation of midspan deflection of the column strip or the middle strip under fixed-end conditions is based on M/EI ratio of the strip to that of the full-width panel

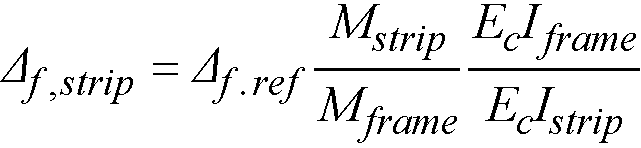      Eq. 2-110

The ratio (M_strip/M_frame) can be considered as a lateral distribution factor, LDF.

For ACI and CSA A23.3-94 codes the lateral distribution factor, LDF, at an exterior negative moment region is

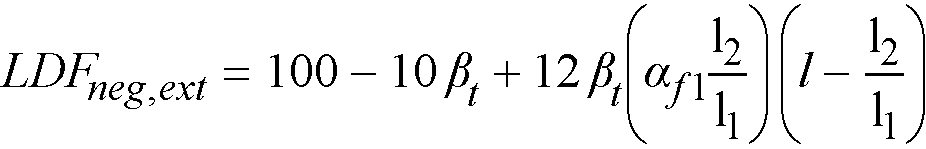      Eq. 211

The LDF at an interior negative moment region is

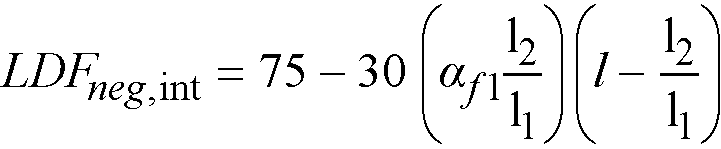      Eq. 2-112

The LDF at a positive moment region is

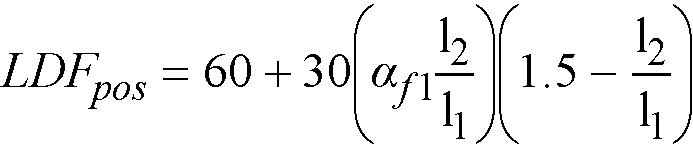      Eq. 2-113

where

a_f1    =    the ratio of flexure stiffness of a beam section to the flexural stiffness of a width of slab bounded laterally by centerlines of adjacent panels on either side of the beam,

b_t    =    ratio of torsional stiffness of an edge beam section to the flexural stiffness of a width of slab equal to the span length of the beam, center-to-center of the supports (see Eq. 2-30).

For CSA A23.3-14/04 code lateral distribution factors are based on tabulated values presented earlier in the chapter.

When a_f1l₂/l₁ is greater than 1.0, a_f1l₂/l₁ will be set equal to 1.0.

The column and middle strip LDF’s can be computed by

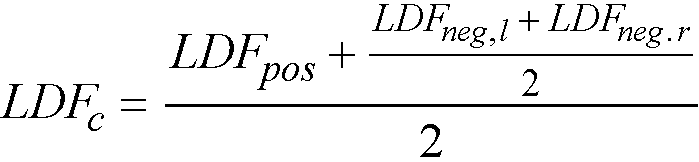      Eq. 2-114

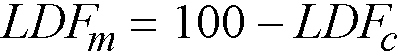      Eq. 2-115

where

LDF_neg,l   =   LDF for the negative moment region at the left end of the span

LDF_neg,r   =   LDF for the negative moment region at the right end of the span

The total midspan deflection for the column or middle strip is the sum of three parts

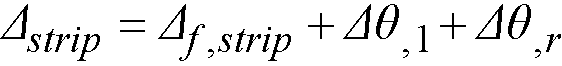      Eq. 2-116

where

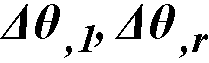= midspan deflection due to rotation of left and right supports, respectively.

The above procedure was implemented starting in v5.00 to follow the reference recommendations exactly and eliminate overestimation of the column strip deflection and underestimation of the middle strip deflection especially for the exterior span.

The deflections should be used in conjunction with the deflections obtained from an analysis in the transverse direction. For square panels (l₁ = l₂), the mid-panel deflection is obtained from the following equation as shown in Figure 2-22

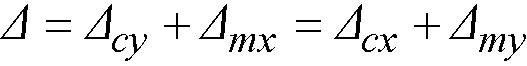      Eq. 2-117

For rectangular panels, (l₁ ¹ l₂), the mid panel deflection is obtained from

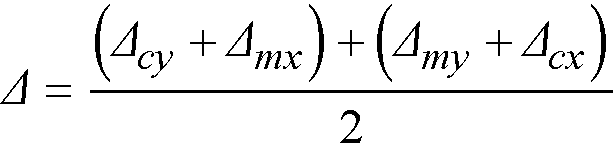      Eq. 2-118

 

Figure 2.23 Deflection computation for a square panel

2.20Material Quantities

The program computes concrete and reinforcing steel quantities. The quantity of concrete is based on an average of the slab, drop, and beam sizes. The total quantity of reinforcing steel computed by the program corresponds to the actual bar sizes and lengths required by design. No allowance is made for bar hooks, anchorage embedment, and so forth. It should be noted that the quantity of reinforcement printed by the program pertains to bending in one direction only. In practice, the total amount of reinforcement for the structure should also include the quantities obtained for the appropriate transverse equivalent frames.

2.21References

[1]Building Code Requirements for Structural Concrete (ACI 318-14) and Commentary (ACI 318R-14), American Concrete Institute, 2014

[2]Building Code Requirements for Structural Concrete (ACI 318-11) and Commentary (ACI 318R-11), American Concrete Institute, 2011

[3]Building Code Requirements for Structural Concrete (ACI 318-08) and Commentary (ACI 318R-08), American Concrete Institute, 2008

[4]Building Code Requirements for Structural Concrete (ACI 318-05) and Commentary (ACI 318R-05), American Concrete Institute, 2005

[5]Building Code Requirements for Structural Concrete (ACI 318-02) and Commentary (ACI 318R-02), American Concrete Institute, 2002

[6]Building Code Requirements for Structural Concrete (ACI 318-99) and Commentary (ACI 318R-99), American Concrete Institute, 1999

[7]Specification for Tolerances for Concrete and Materials and Commentary, An ACI Standard (ACI 117-06), American Concrete Institute, 2006

[8]National Building Code of Canada 2010, Volume 2, Canadian Commission on Buildings and Fire Codes, National Research Council of Canada, 2010

[9]National Building Code of Canada 2005, Volume 1, Canadian Commission on Buildings and Fire Codes, National Research Council of Canada, 2005

[10]A23.3-14, Design of Concrete Structures, Canadian Standards Association, 2014.

[11]A23.3-04, Design of Concrete Structures, Canadian Standards Association, 2004.

[12]Explanatory Notes on CSA Standard A23.3-04 in Concrete Design Handbook, Third Edition, Cement Association of Canada, 2006

[13]A23.3-94, Design of Concrete Structures, Canadian Standards Association, 1994 (Reaffirmed 2000).

[14]Explanatory Notes on CSA Standard A23.3-94 in Concrete Design Handbook, Second Edition, Canadian Portland Cement Association, 1995

[15]Wight J.K., MacGregor J.G., Reinforced Concrete, Mechanics and Design, Fifth Edition, Pearson Prentice Hall, 2009

[16]MacGregor J.G., Bartlett F.M., Reinforced Concrete – Mechanics and Design, First Canadian Edition, Prentice Hall Canada Inc., 2000

[17]Branson, D. E., Instantaneous and Time-Dependent Deflections of Simple and Continuous Reinforced Concrete Beams, HPR Report No. 7, Pt. I, Alabama Highway Department in Cooperation with U.S. Department of Commerce, Bureau of Public Roads, August 1965.

[18]Notes on ACI 318-05 Building Code Requirements for Structural Concrete with Design Applications, Edited by Mahmoud E. Kamara and Basile G. Rabbat, Portland Cement Association, 2005

[19]Control of Deflection in Concrete Structures (ACI 435R-95), Reported by ACI Committee 435, American Concrete Institute, 1995 (Reapproved 2000).

[20]ACI Committee 435, Subcommittee 7, Deflections of Continuous Concrete Beams, Journal of the American Concrete Institute, Proceedings V. 70, No. 12, December 1973, pp. 781-787.

[21]Nilson, A. H., and Walters, D. B., Jr., Deflection of Two-Way Floor Systems by the Equivalent Frame Method, Journal of the American Concrete Institute, Proceedings, V. 72, No. 5, May, 1975, pp. 210-218.

[22]ACI Committee 435, State-of-the-Art Report, Deflection of Two-Way Floor Systems, Special Publication SP43-3, American Concrete Institute, 1974.

[23]Kripanarayanan, K. M., and Branson, D. E., Short-Time Deflections of Flat Plates, Flat Slabs and Two-Way Slabs, Journal of the American Concrete Institute, Proceedings, V. 73, No. 12, December 1976, pp. 686-690.

[24]Wight, J. K., Falconer, D., Checking Punching Shear Strength by the ACI Code, Concrete International, November 2005, pp. 76.

[25]Park, W. and Gamble, W. L., Reinforced Concrete Slabs, Second Edition, John Wiley & Sons, Inc., 2000