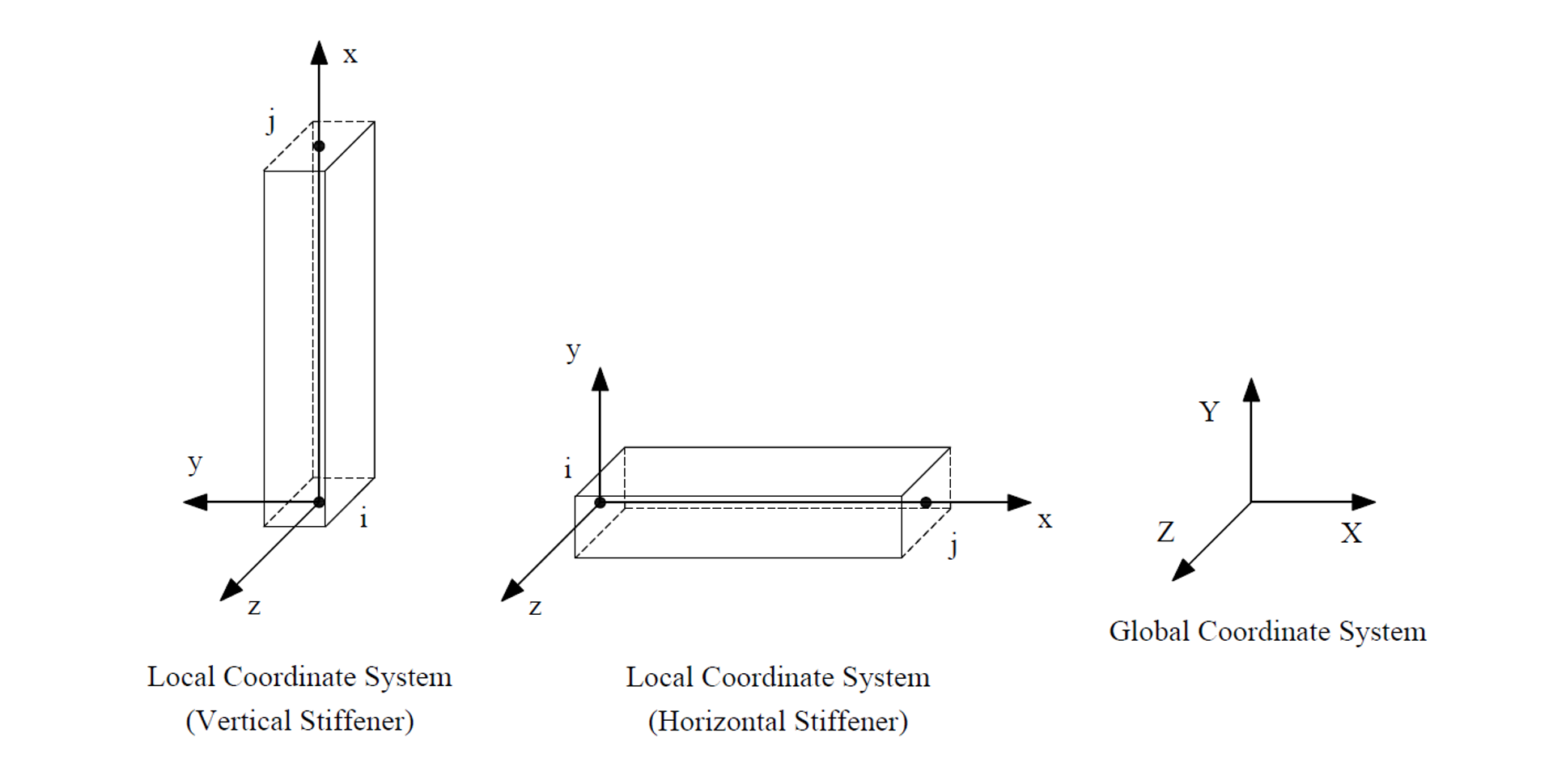
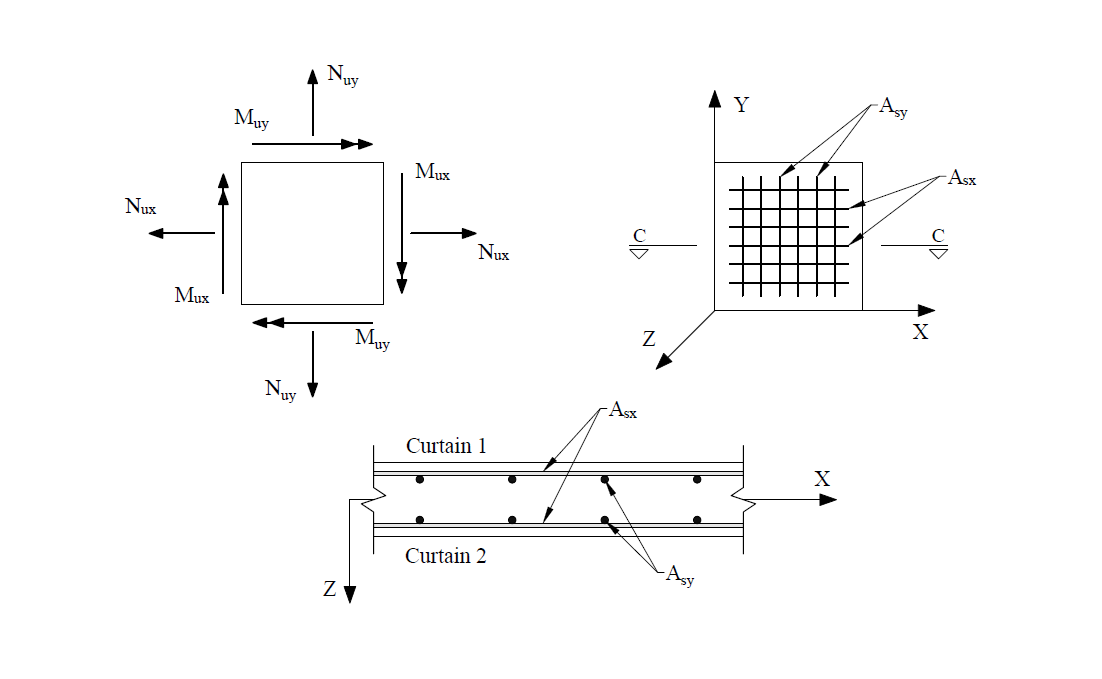
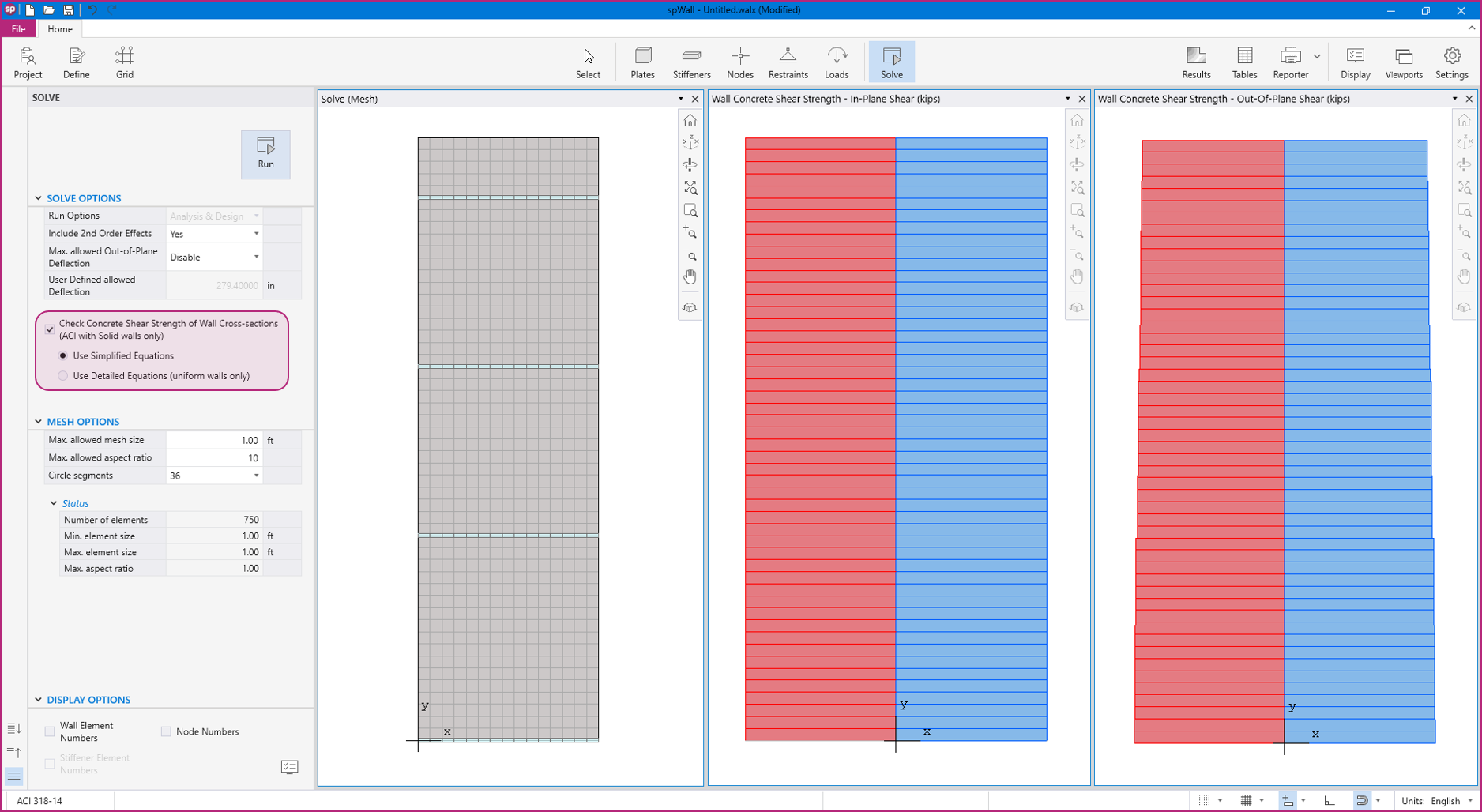
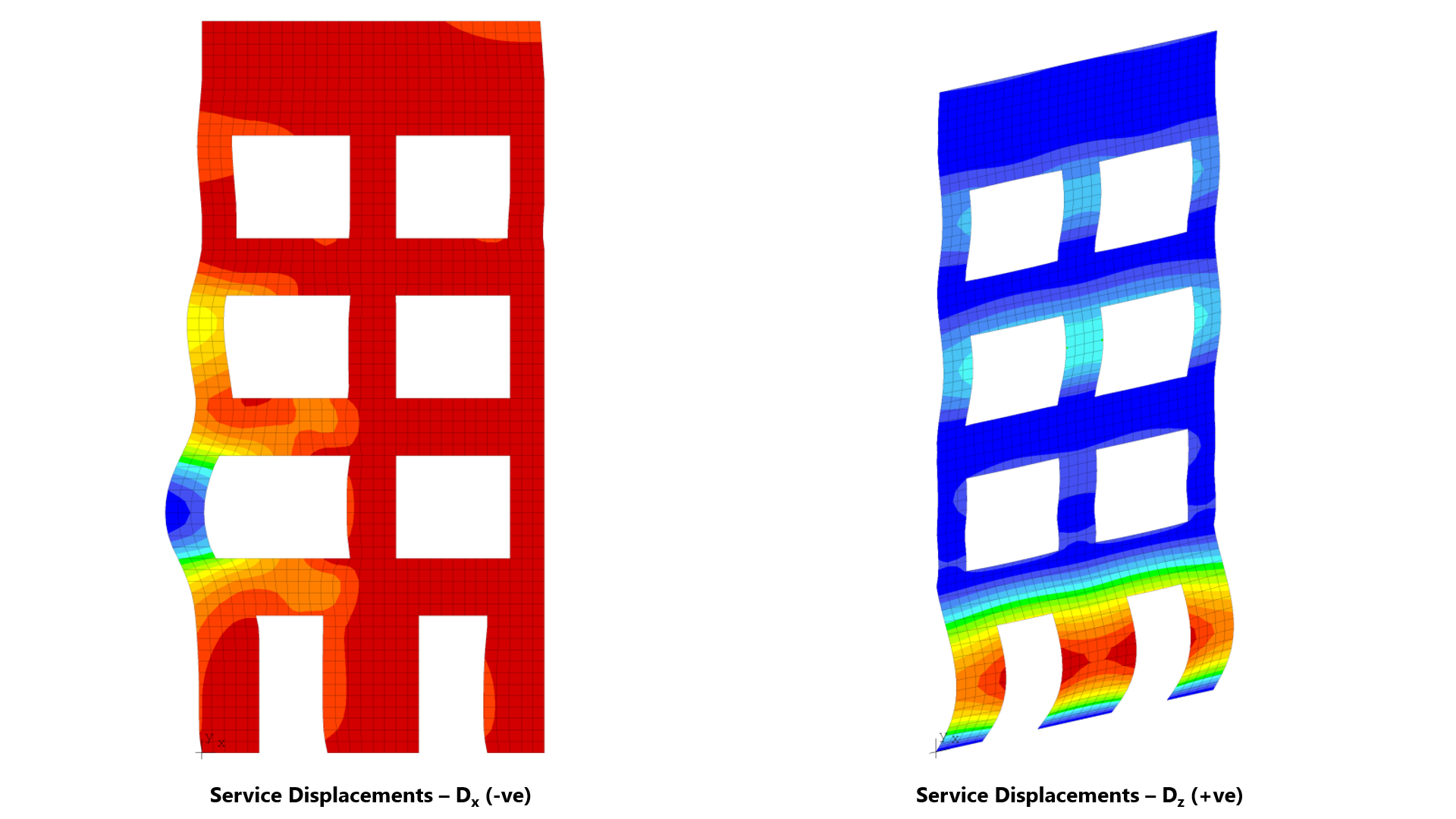
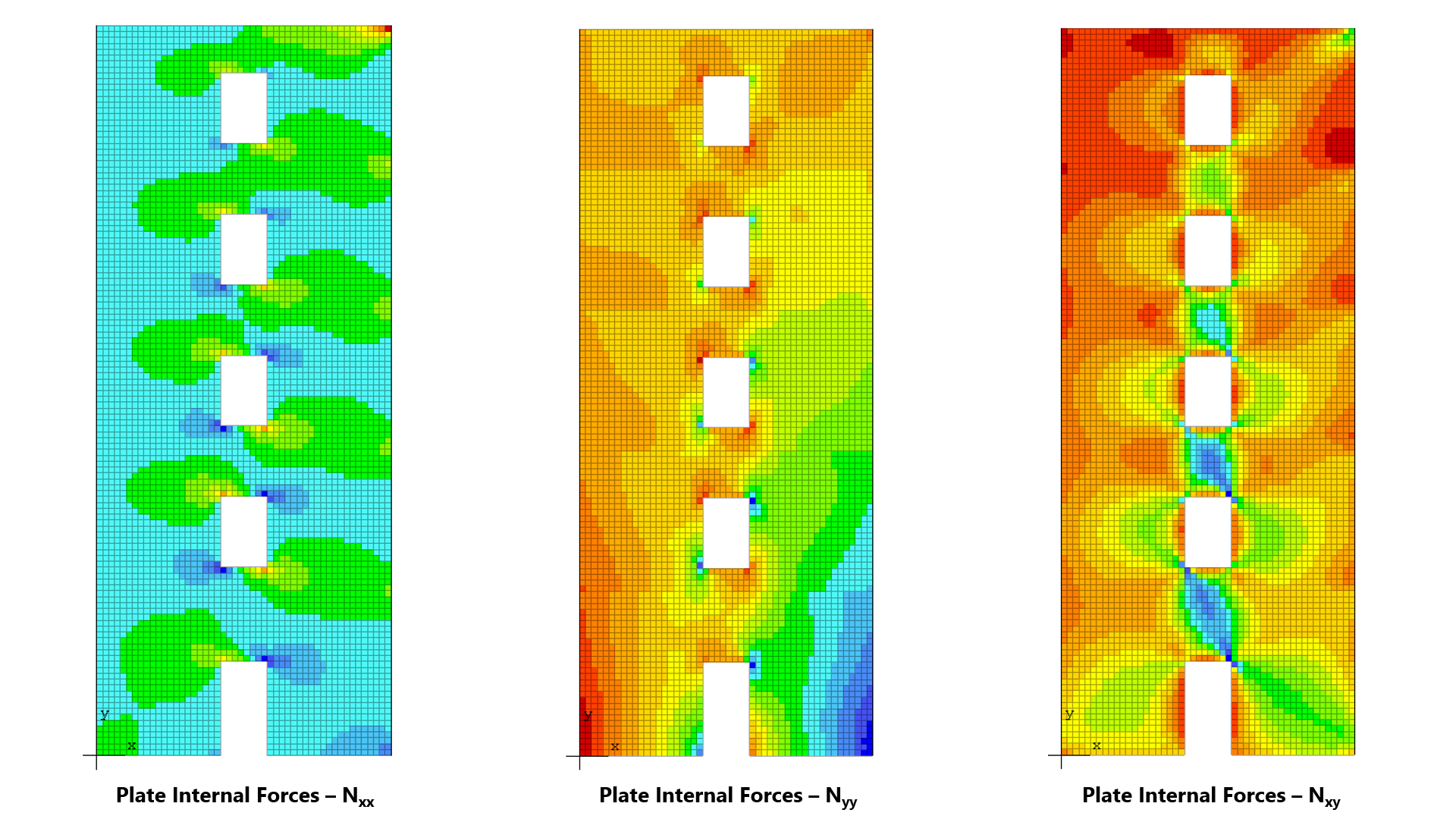
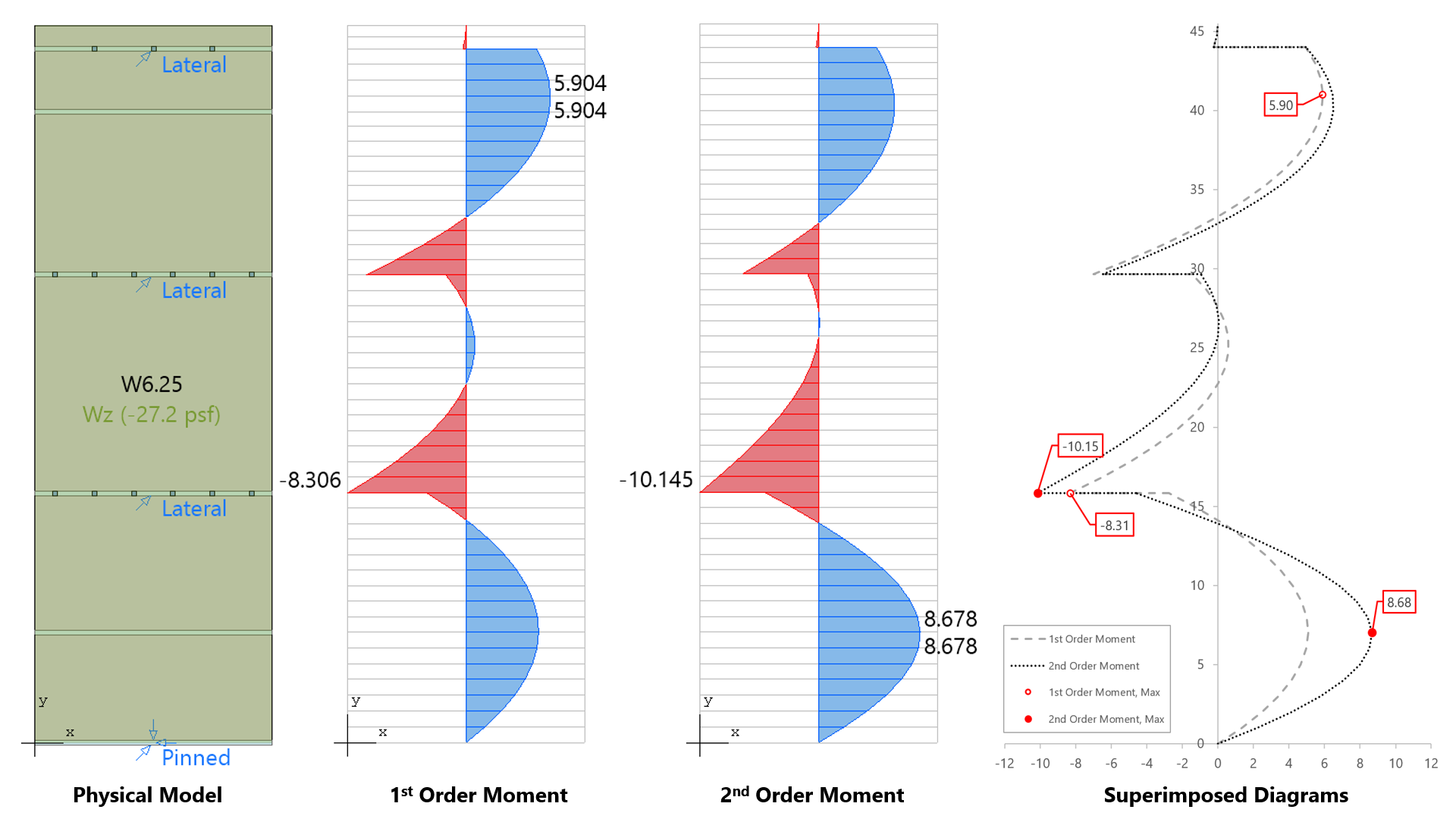
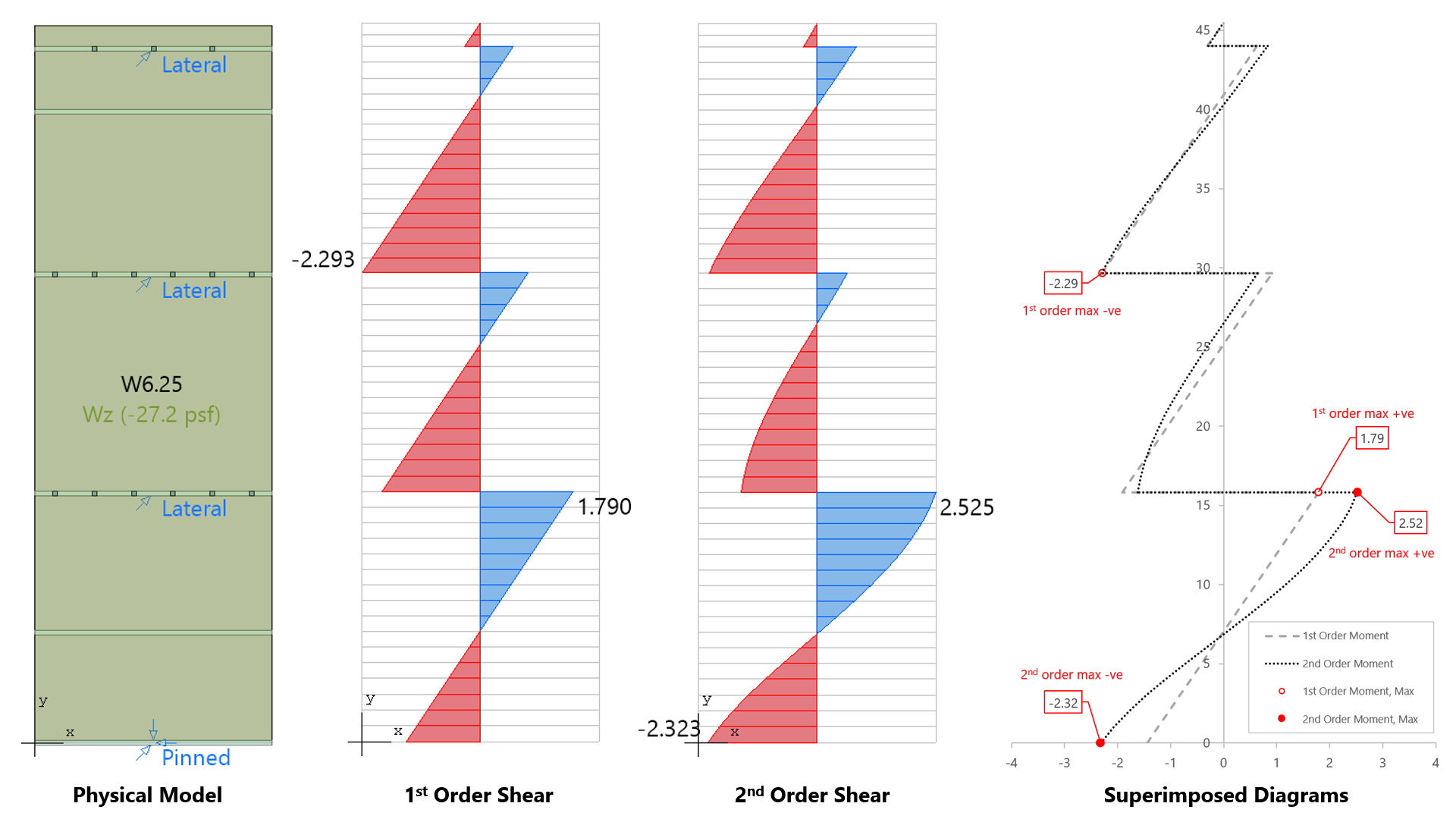
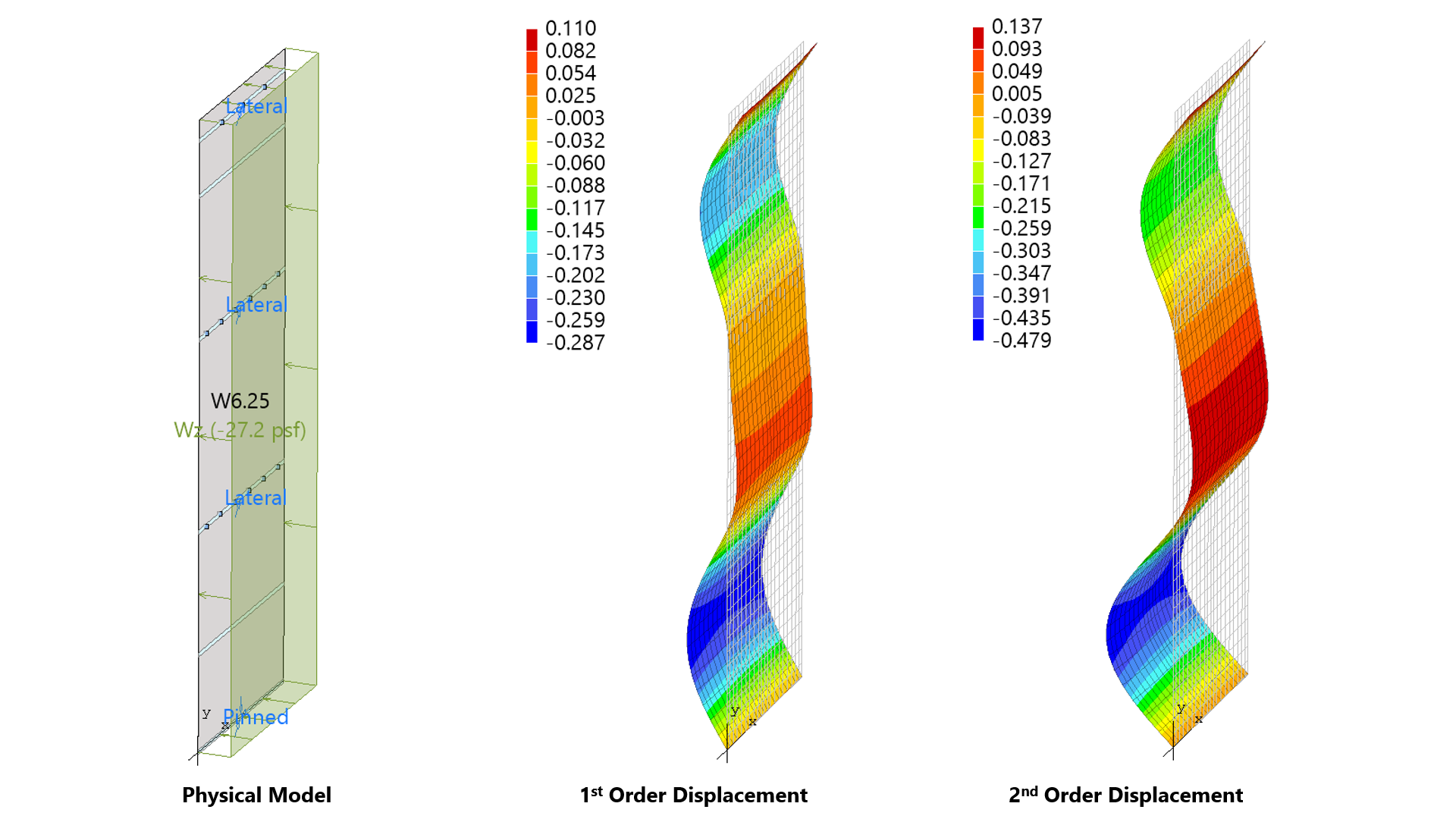
spWall can perform second-order analysis in which the effect of in-plane forces are taken into account on the out-of-plane deflections. If second order analysis is requested (the default setting), a complete analysis cycle is done for each load combination. In each cycle, the basic stiffeness terms of plate elements are modified to account for the effect of membrane forces. For stiffener elements, the basic stiffness matrix is modified to account for the effect of axial forces.
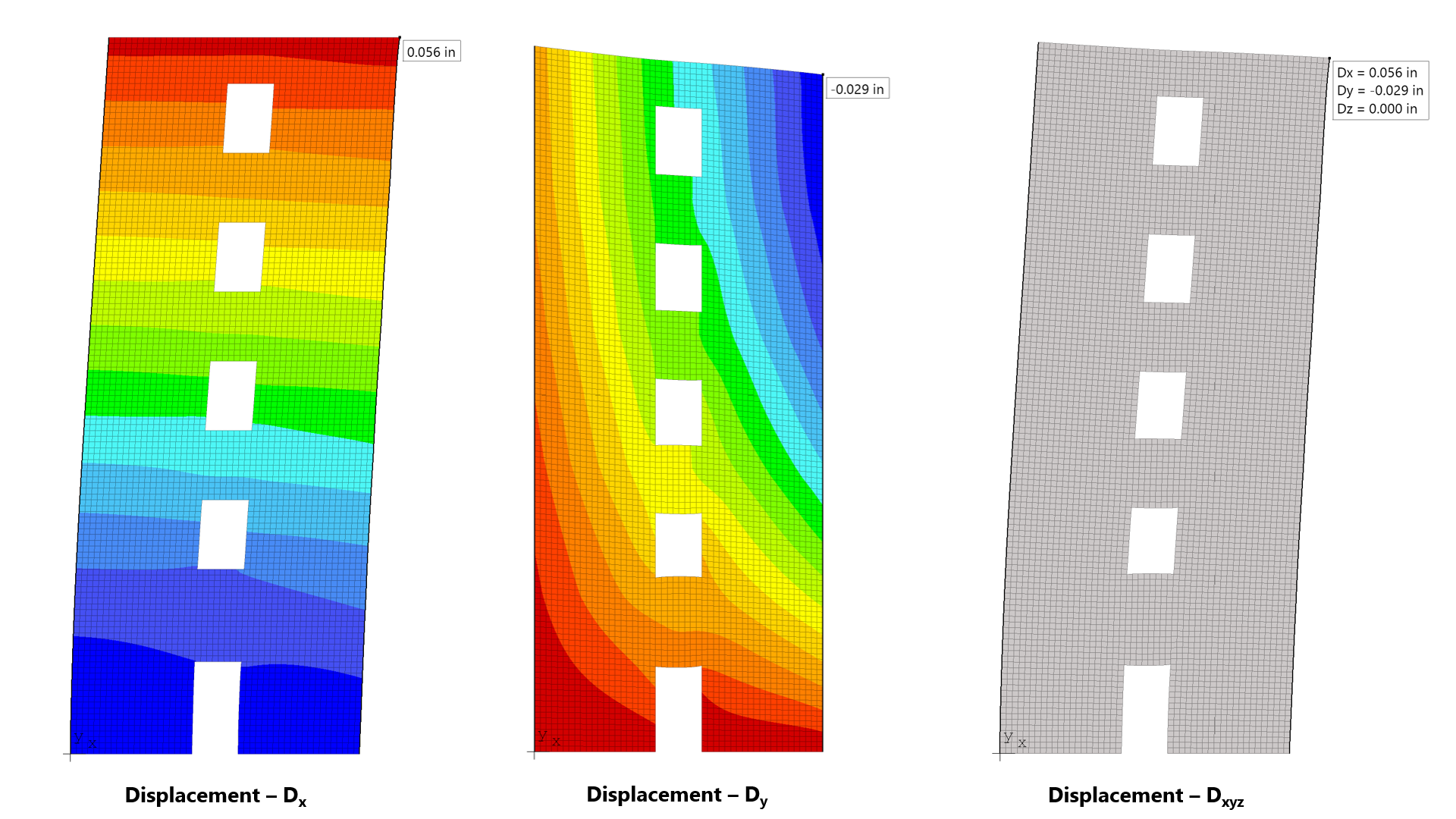
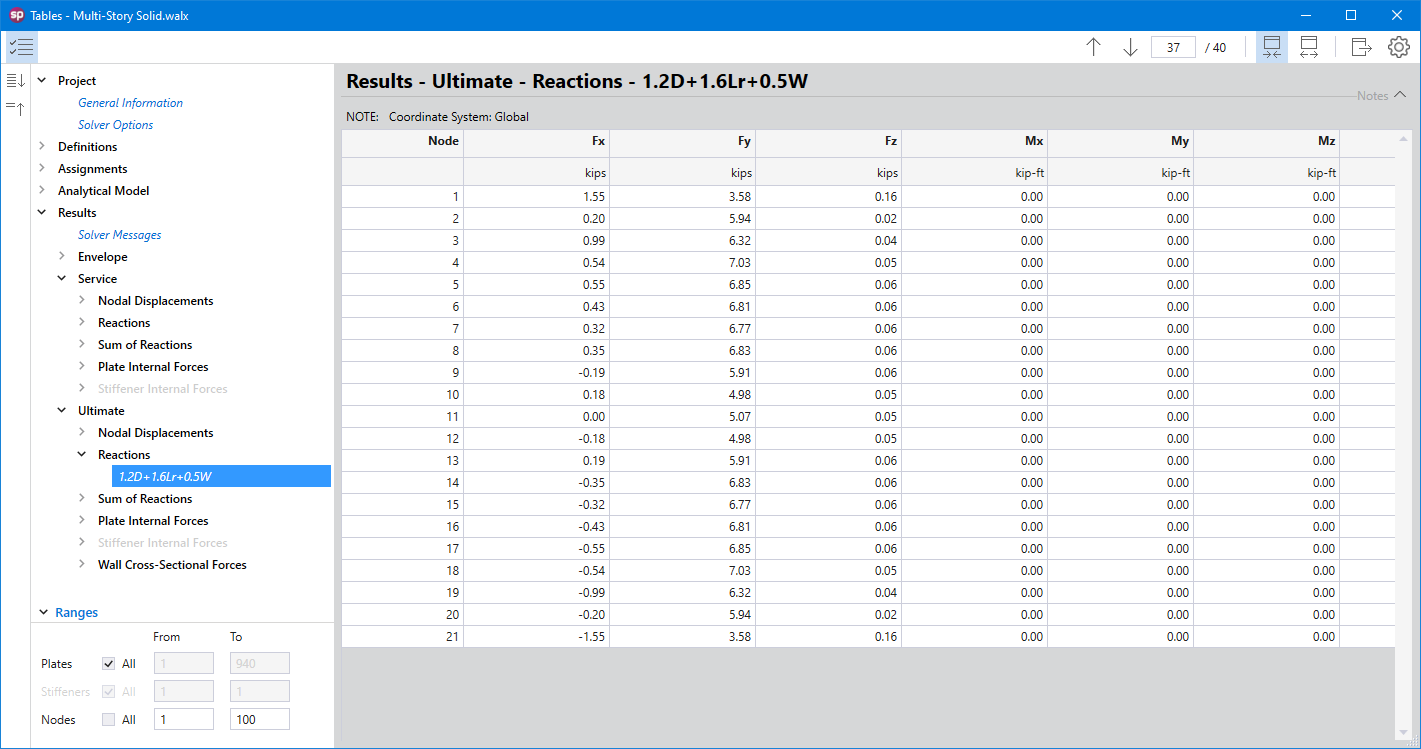
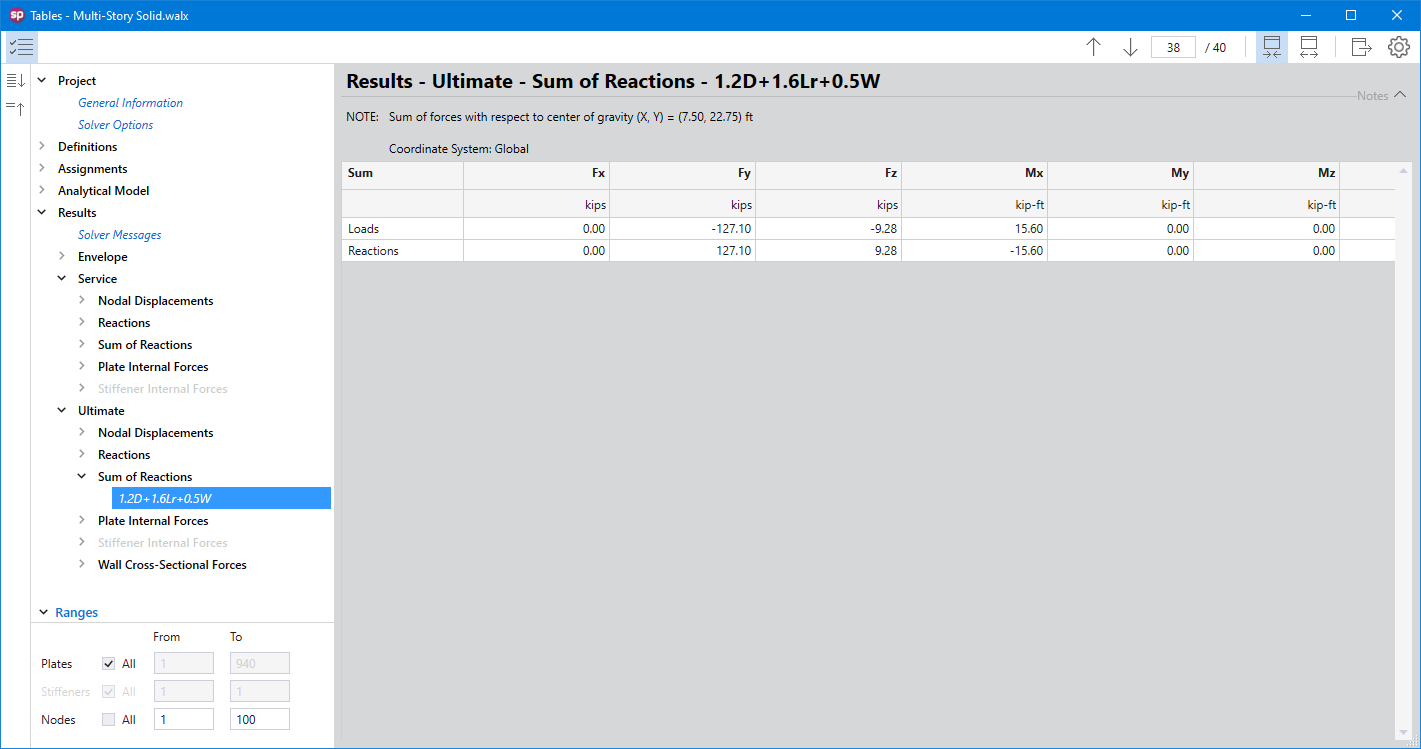
spWall reports the restraint and Nodal Spring reactions for individual service load and ultimate load combinations for nodes with specified restraints or nodal springs. Nodal translational reactions Fx, Fy, and Fz and rotational reactions Mx, My, and Mz are output. Positive translational reactions are in the direction of the positive axes and positive moment reactions are determined using the right-hand rule. The program also reports sum of forces and moments (with respect to wall center of gravity) for applied loads and reactions.
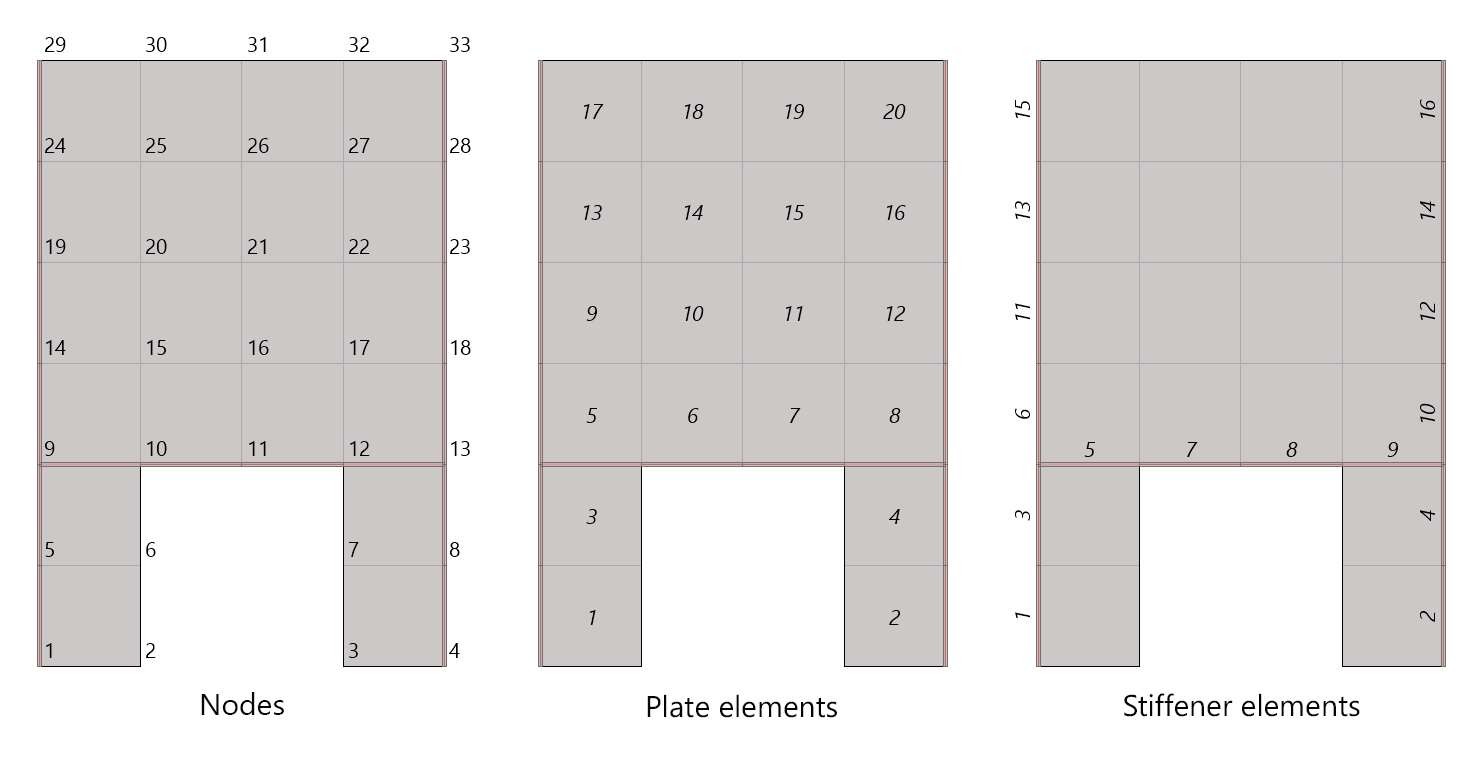
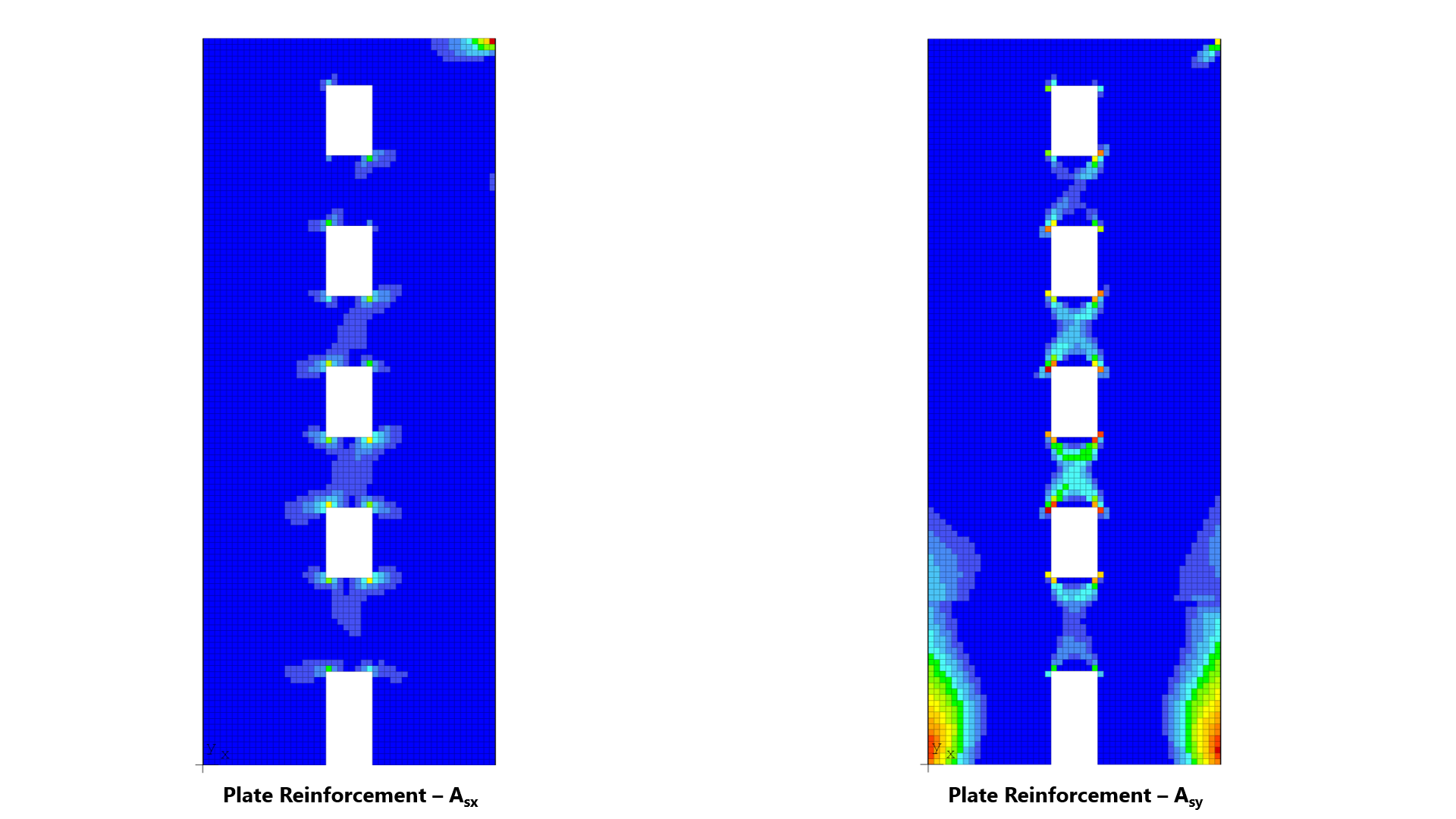
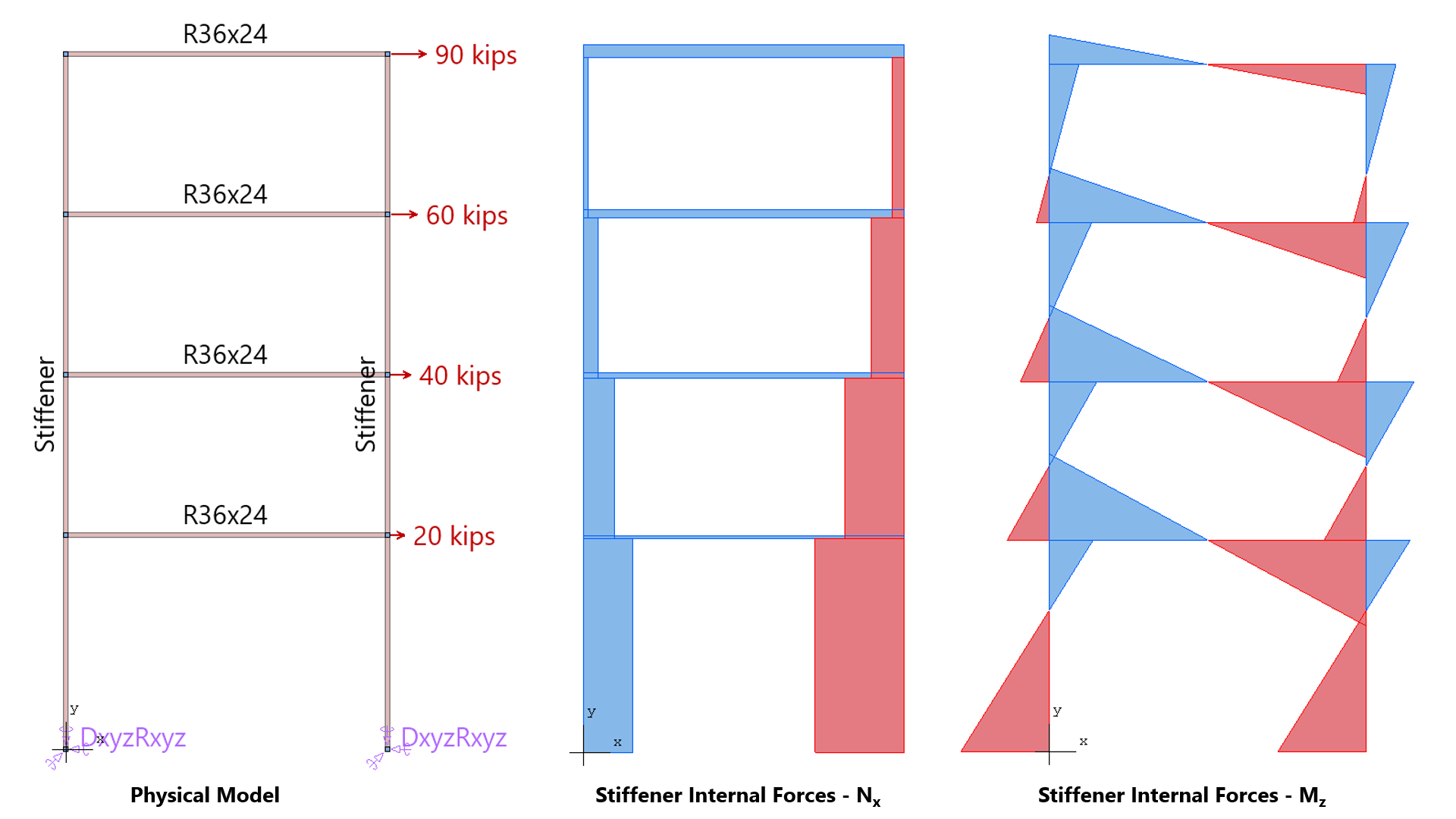
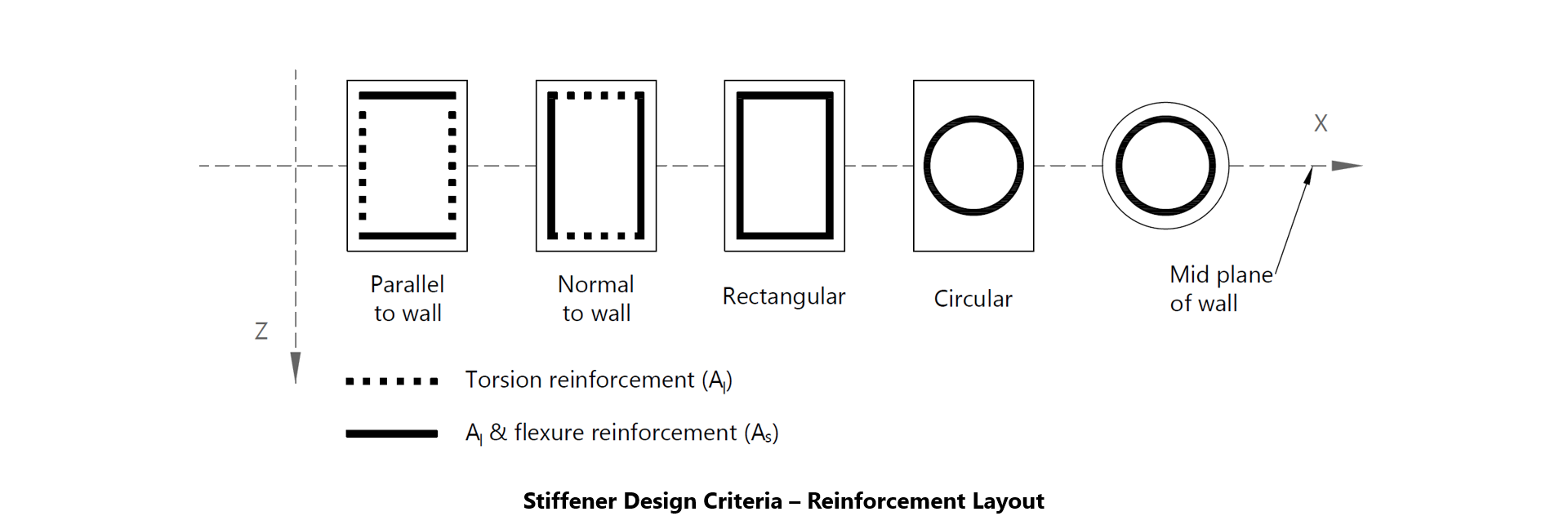
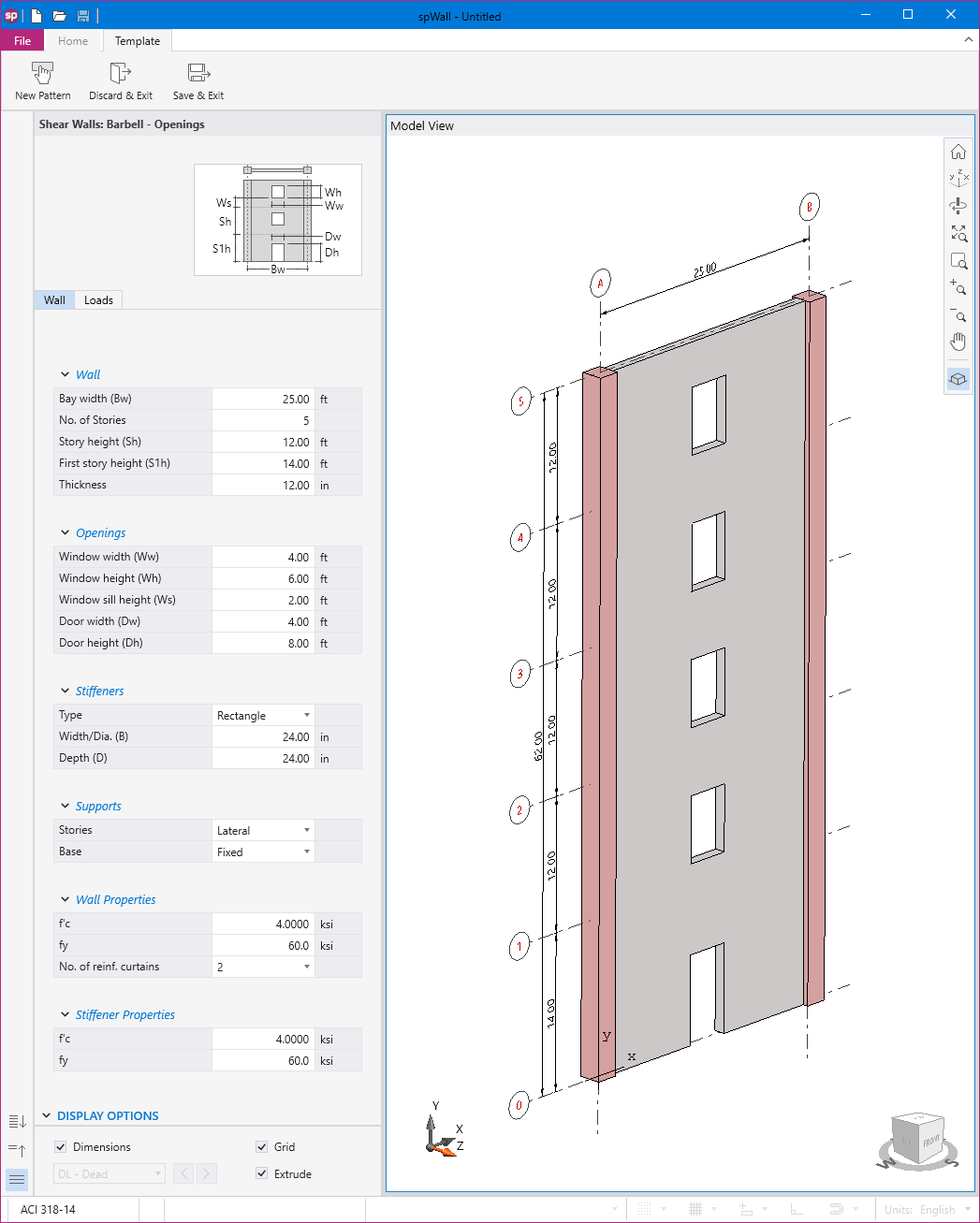
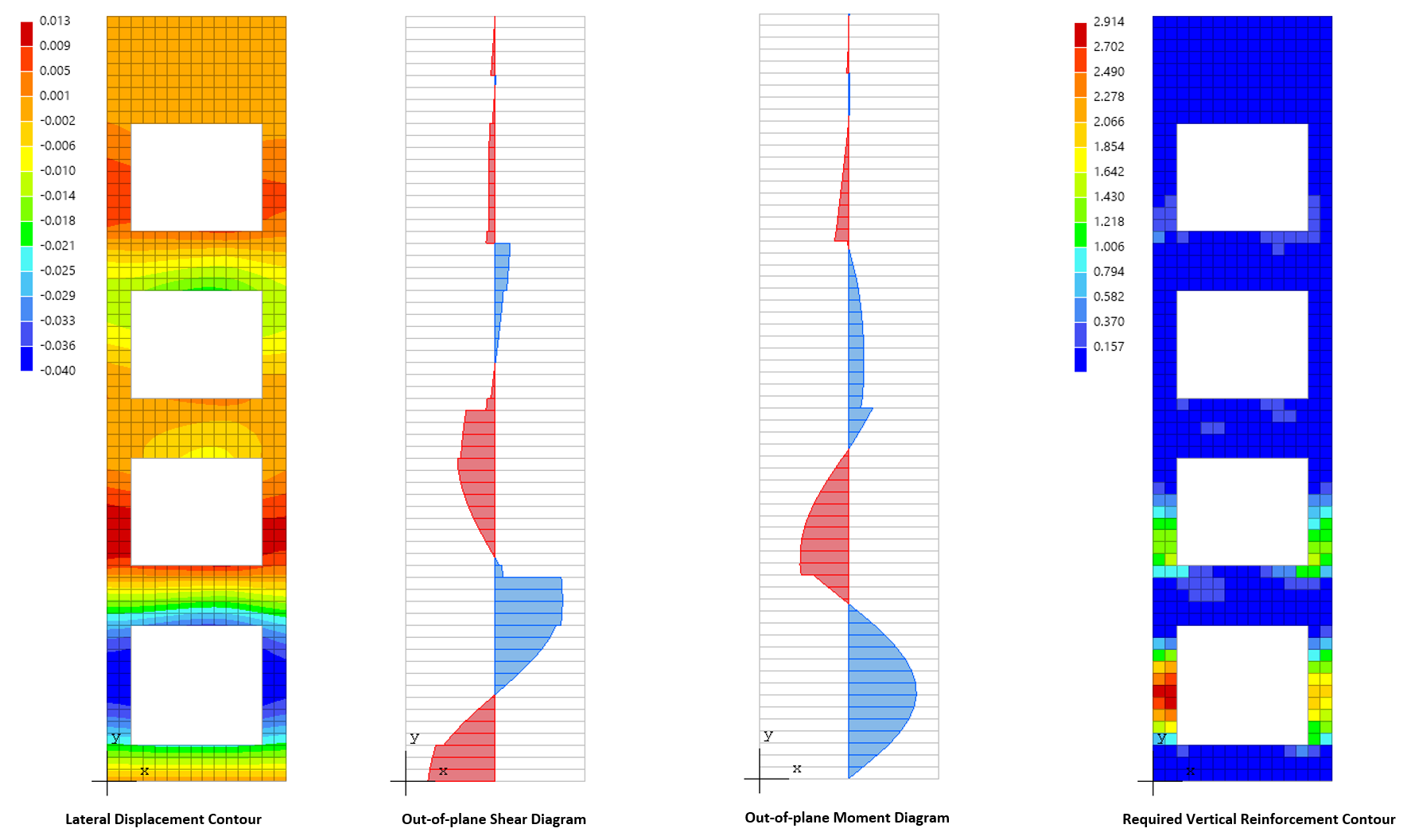
Stiffener elements can be used to model beams or columns that are embedded in the wall to increase its structural capacity, e.g. lintels, pilasters, and boundary elements of shear walls. Wall piers that are required to be designed as columns can also be modeled using stiffeners. Additionally, isolated stiffener elements placed outside of the wall can model rigid frame structures attached to the wall. The program will calculate internal forced in the stiffener elements and calculate the area of reinforcement required for axial action combined with biaxial bending as well as shear and torsion.
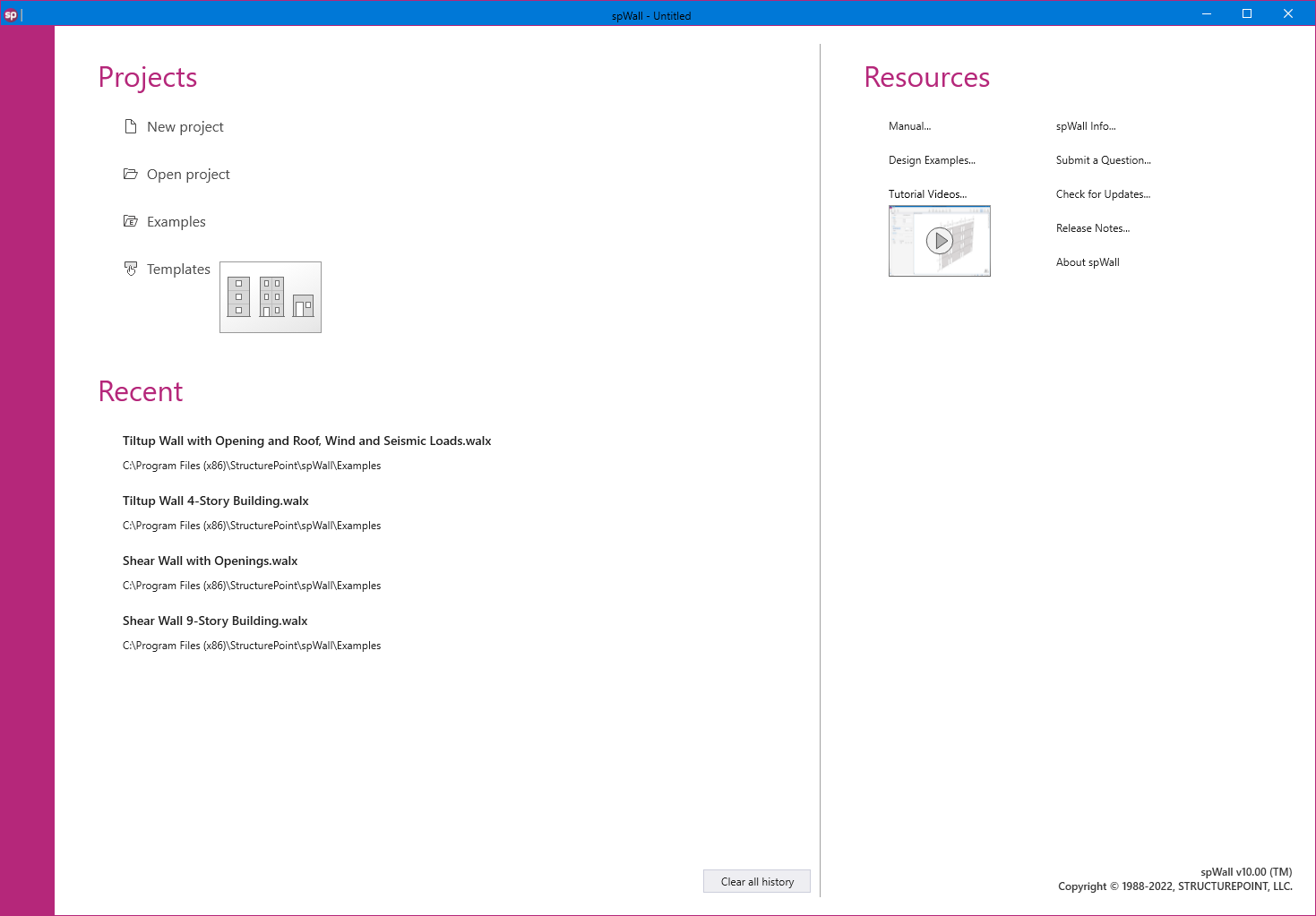
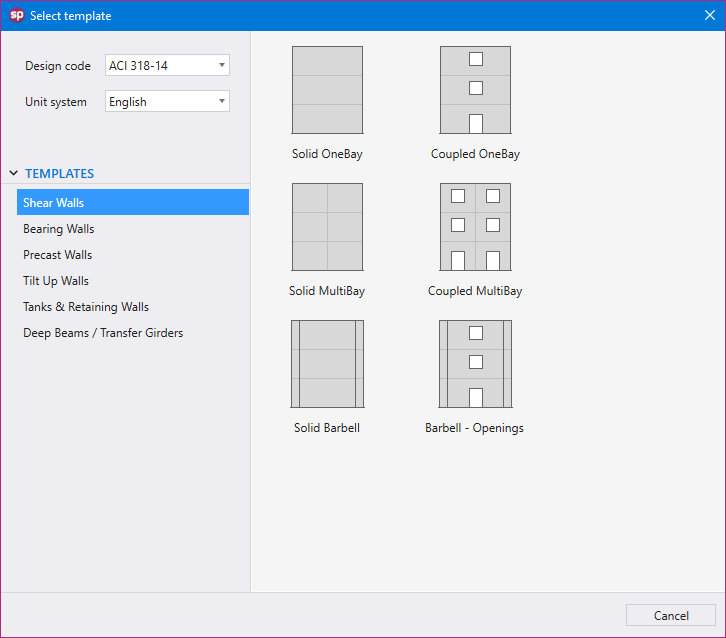
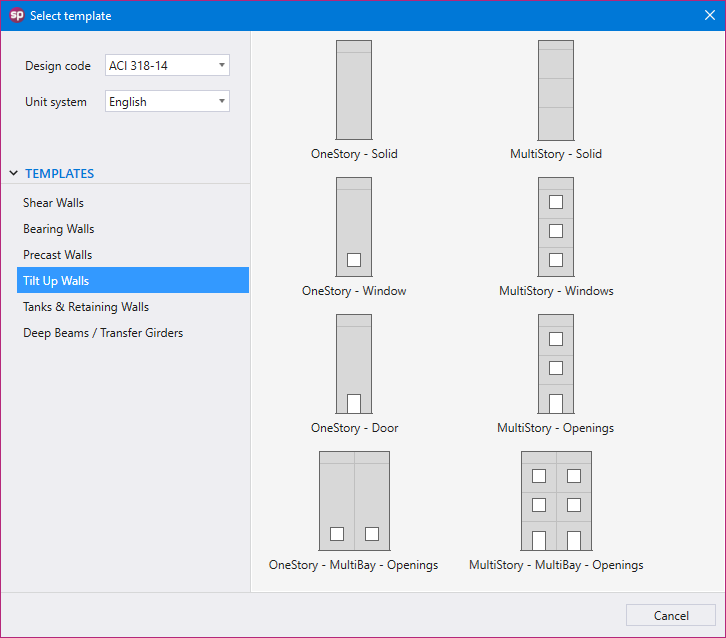
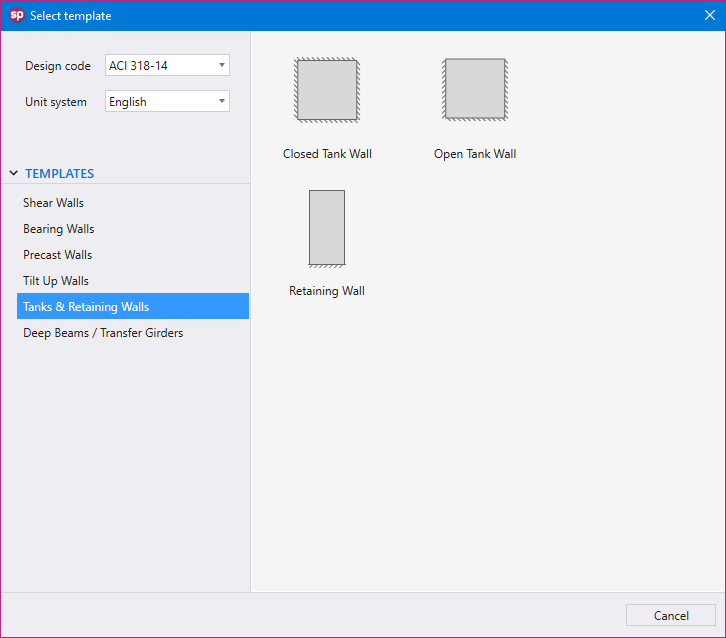
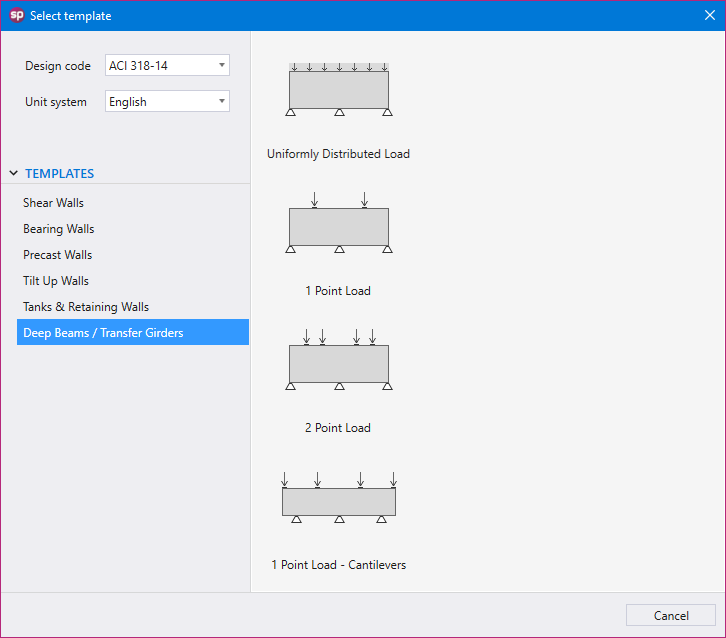
Utilizing Templates is a quick and simple option for new models in spWall. The user can select from a set of pre-defined templates and edit their properties for simple and quick model generation.
Each template focuses on a particular structural shape with a specific loading pattern. The user can edit the geometric dimensions of the shape, applied loads, boundary conditions, and material properties. Other shape specific options may also be available for some templates.
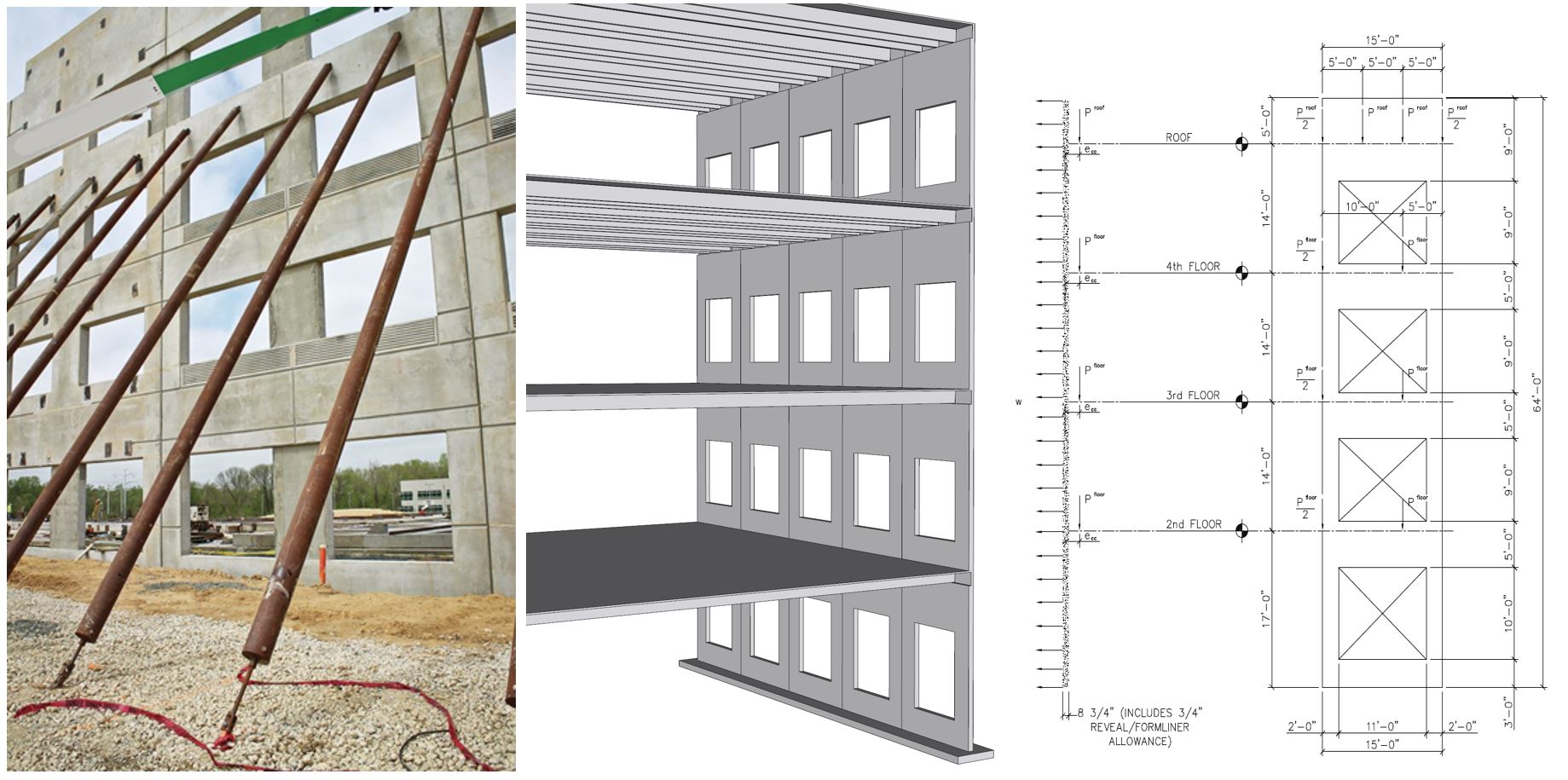
Tilt-up is a form of construction with increasing popularity owing to its flexibility and economics. Tilt-up concrete is essentially a precast concrete that is site cast instead of traditional factory cast concrete members.
The construction of tilt-up walls involves pouring the walls horizontally on the building's floor slab at the job site. A crane hoists the panels into a place where steel braces temporarily secure the panels until workers can weld permanent fasteners into the panel's joints, footing, and roofline.
The design guide for tilt-up concrete panels, ACI 551, states that tilt-up concrete walls can be analyzed using the provisions of ACI 318 - Alternative Analysis (Design) Method. Most walls, and especially slender walls, are widely evaluated using this method. The method is applicable when the conditions summarized below are met:
- The cross section shall be constant over the height of the wall
- The wall can be designed as simply supported
- Maximum moments and deflections occurring at midspan
- The wall must be axially loaded
- The wall must be subjected to an out-of-plane uniform lateral load
- The wall shall be tension-controlled
- The reinforcement shall provide design strength greater than cracking strength
ACI 318 provides the alternative design method as a simple and accurate option for analysis and design of simple walls meeting the method conditions. ACI 551 allows the use of this method for some cases even though some of the method limitations are not satisfied as long as the results obtained are still within acceptable ranges. However, some walls with complex geometries (multi-span continuous walls with the presence of openings) bring a lot of challenges accompanied with the use of the alternative analysis (design) method.
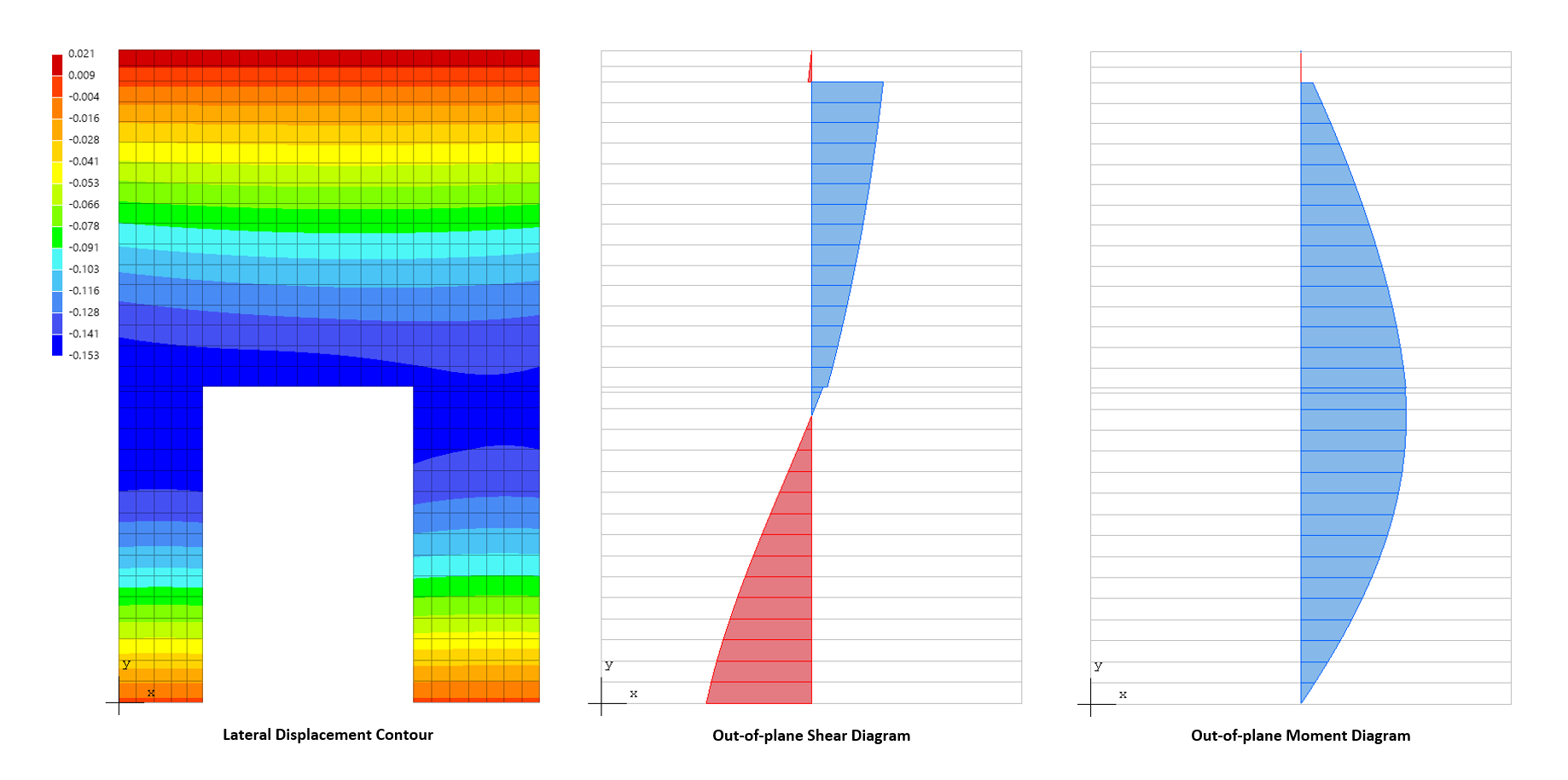
To understand the wall behavior and adequately address strength and stability requirement, other methods such as finite element analysis, utilized in spWall, can be used. Many other issues arise with panels not meeting the method limitations (continuous and cantilevered walls, variable thickness and width, wall with openings, non-standard boundary conditions, walls with high compressive loads, in-plane lateral loads, non-standard concentrated load position from attachments of piping, racking etc., concentrated out of plane loads).
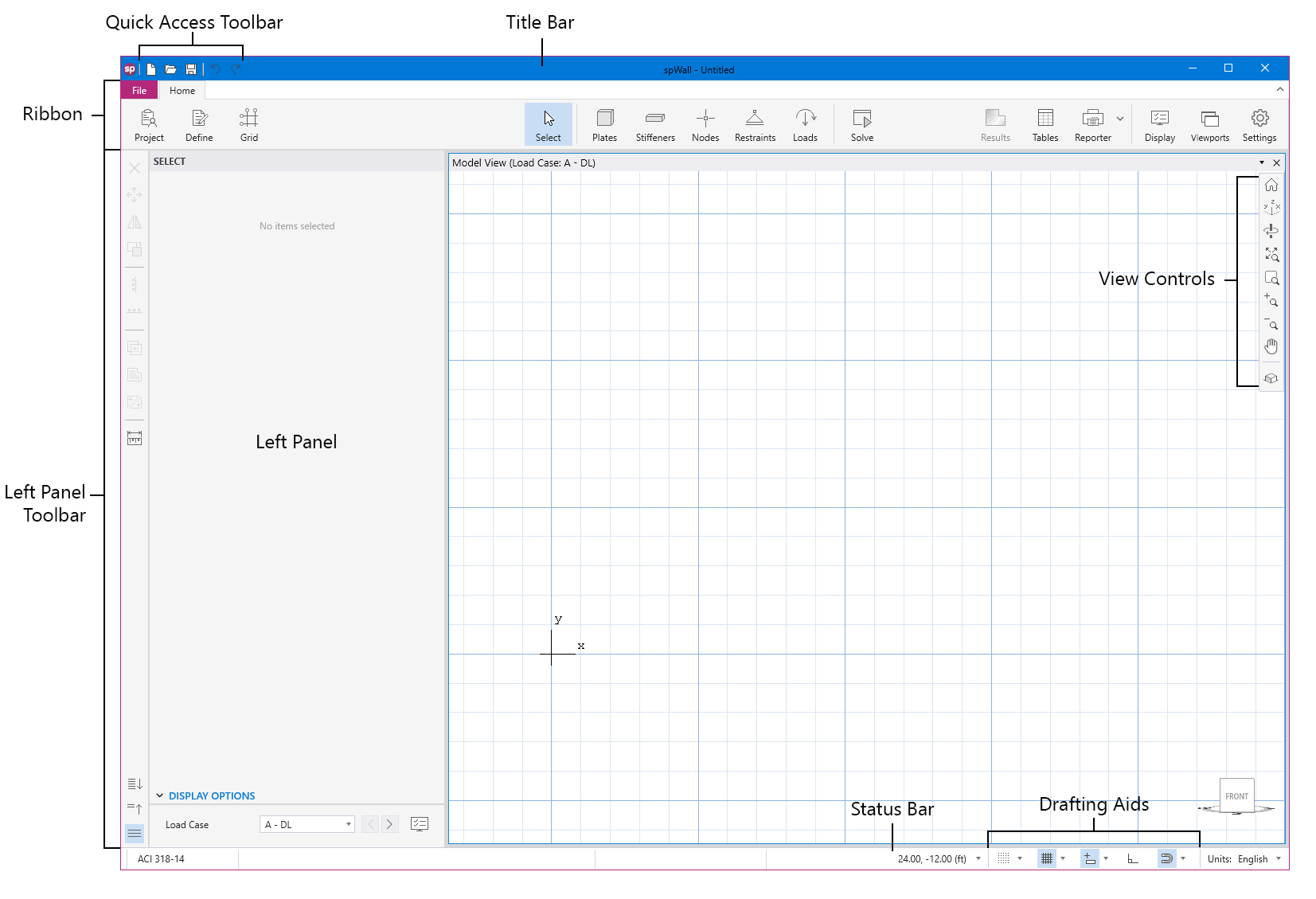
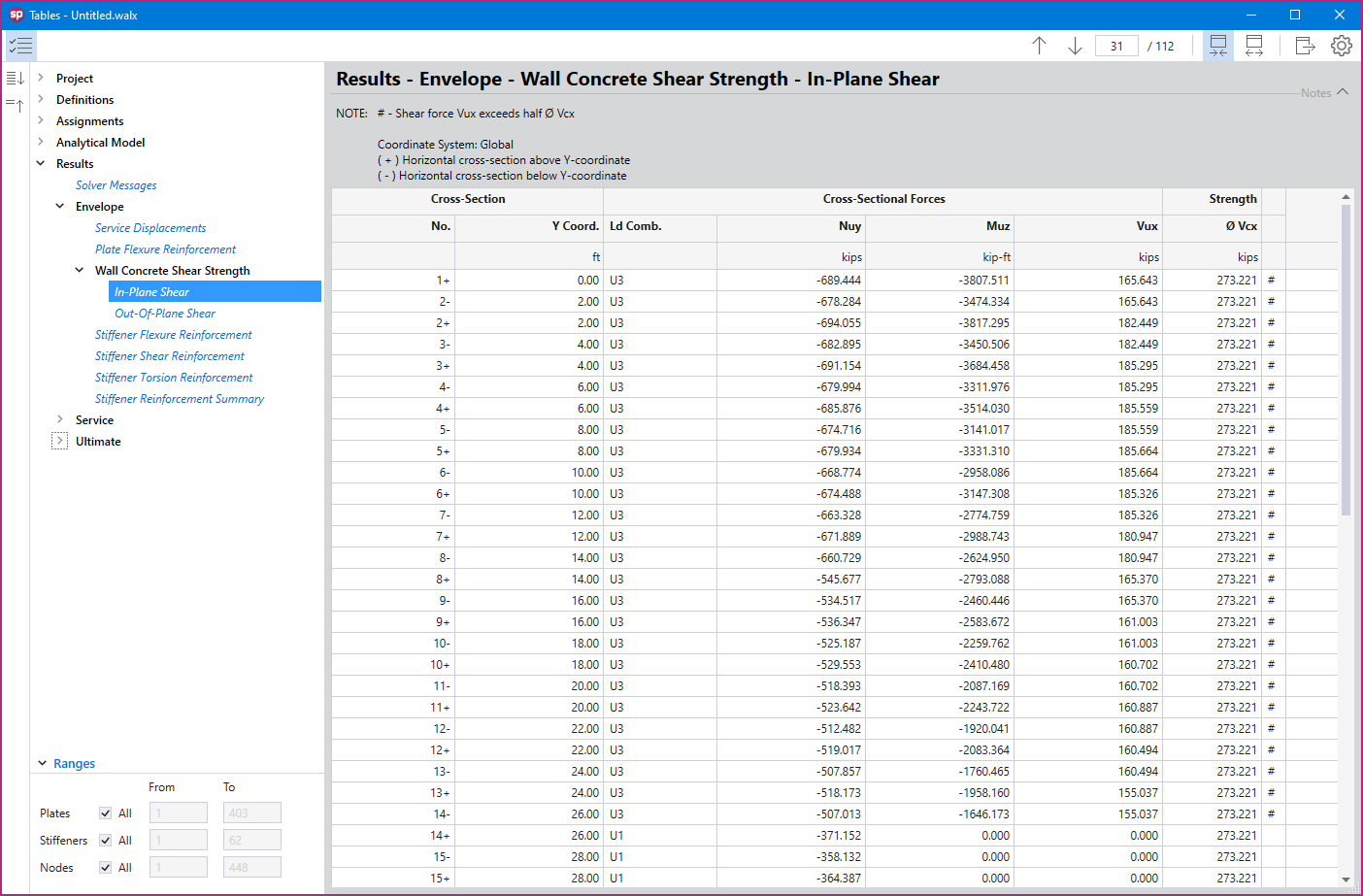
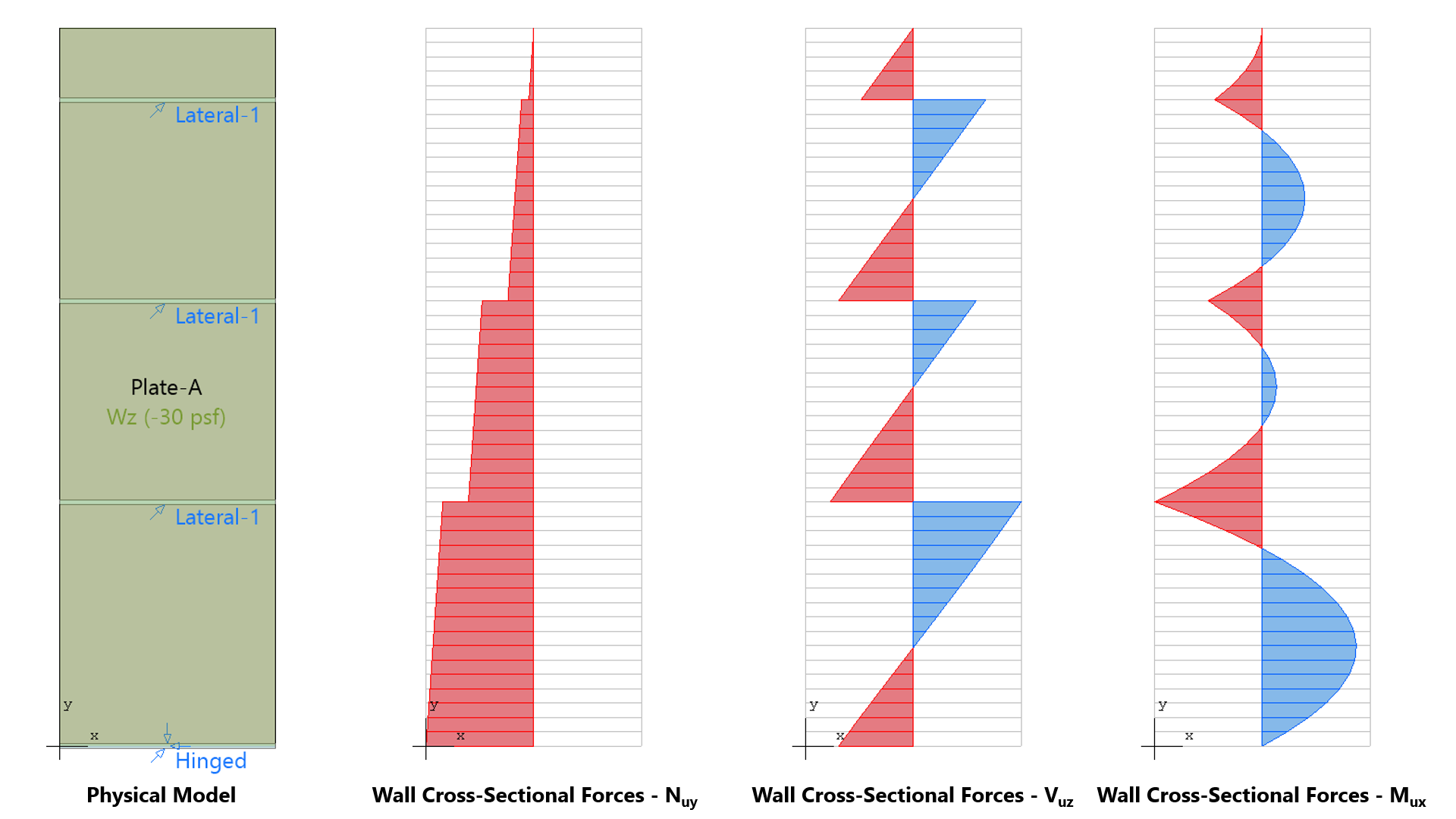
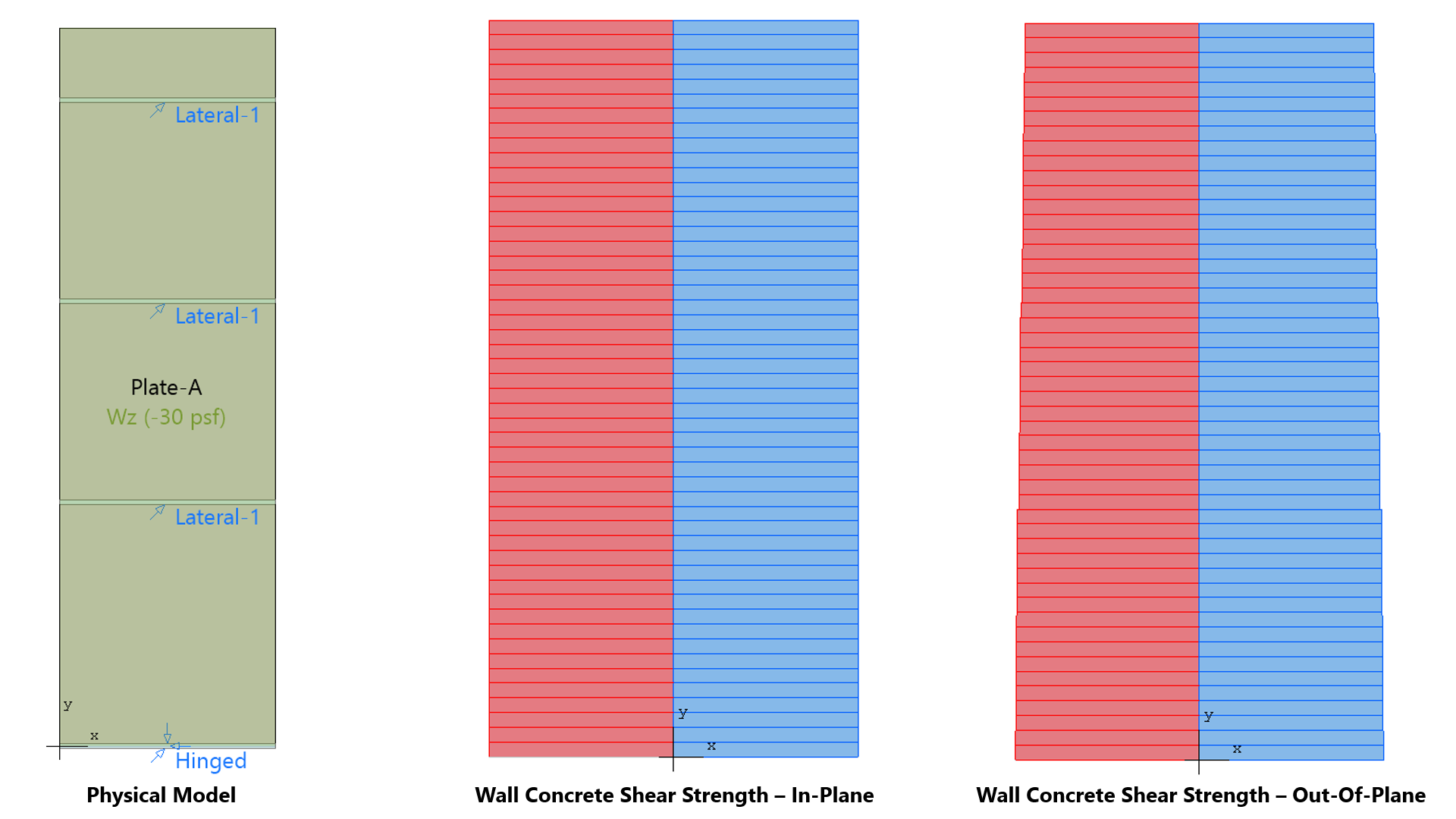
spWall uses the Finite Element Method for the structural modeling, analysis, and design of slender and non-slender reinforced concrete walls (including tilt-up walls) subjected to static loading conditions. The wall is idealized as a mesh of rectangular plate elements and straight line stiffener elements. The program calculates the required amount of reinforcement in the plate elements and stiffener elements based on the design code selected by the user. For solid walls, spWall can also compare cross sectional shear forces with calculated in-plane and out-of plane shear strength provided by concrete.
Software
spColumn v10.20spMats v10.00spWall v10.20spSlab v10.00spBeam v10.00spFrame v1.50MaintenanceNetwork LicensingDownload & Buy
Buy Now! Download Trial Shopping Cart Pay Invoice