StructurePoint - spColumn Features

Home: Software: spColumn v10.10: Features

Features

spColumn User Interface

Start Screen

Main Window

Tables

Reporter Window

Print/Export Window

To the top

Analysis & Design

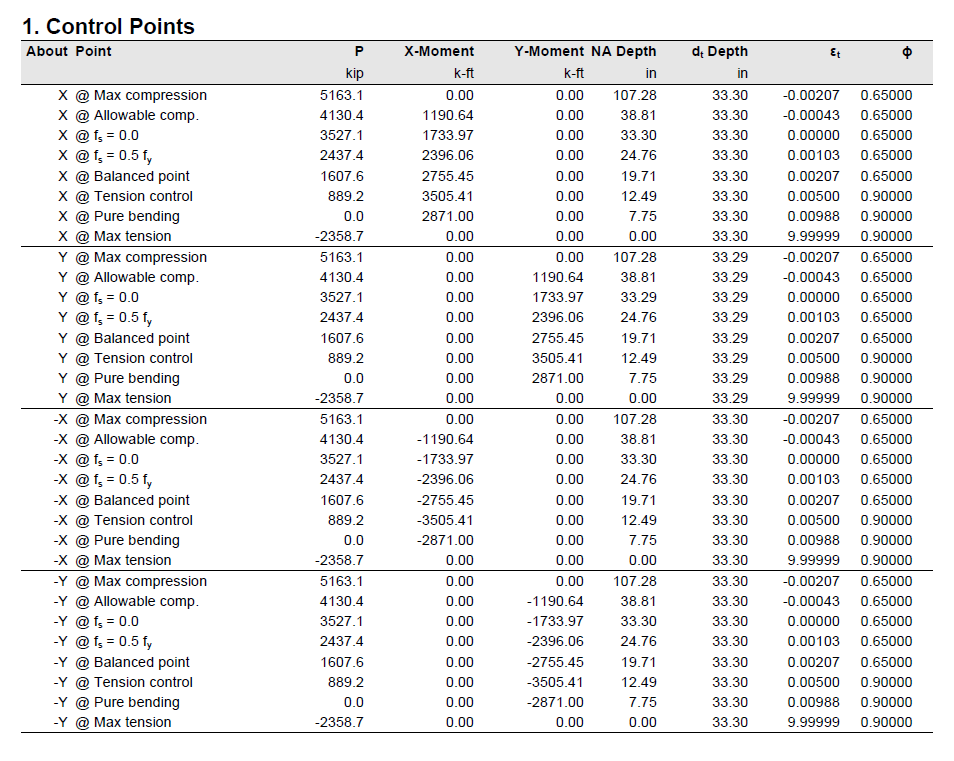
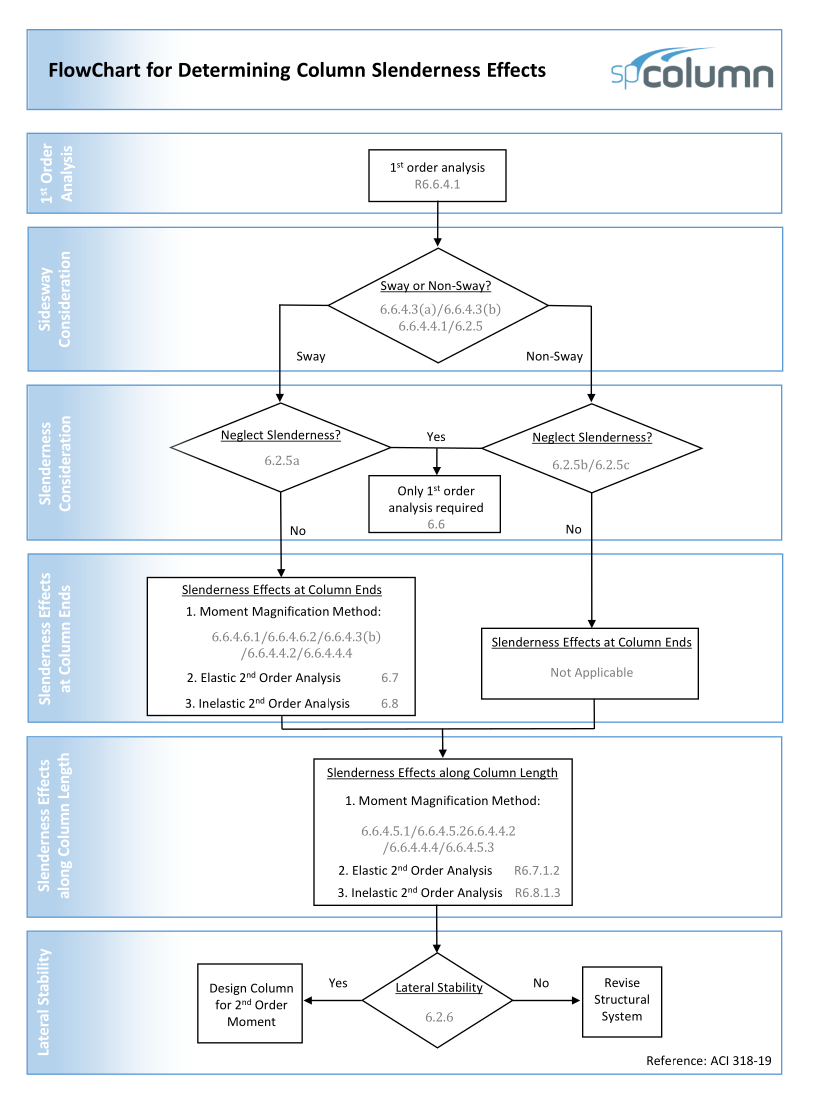
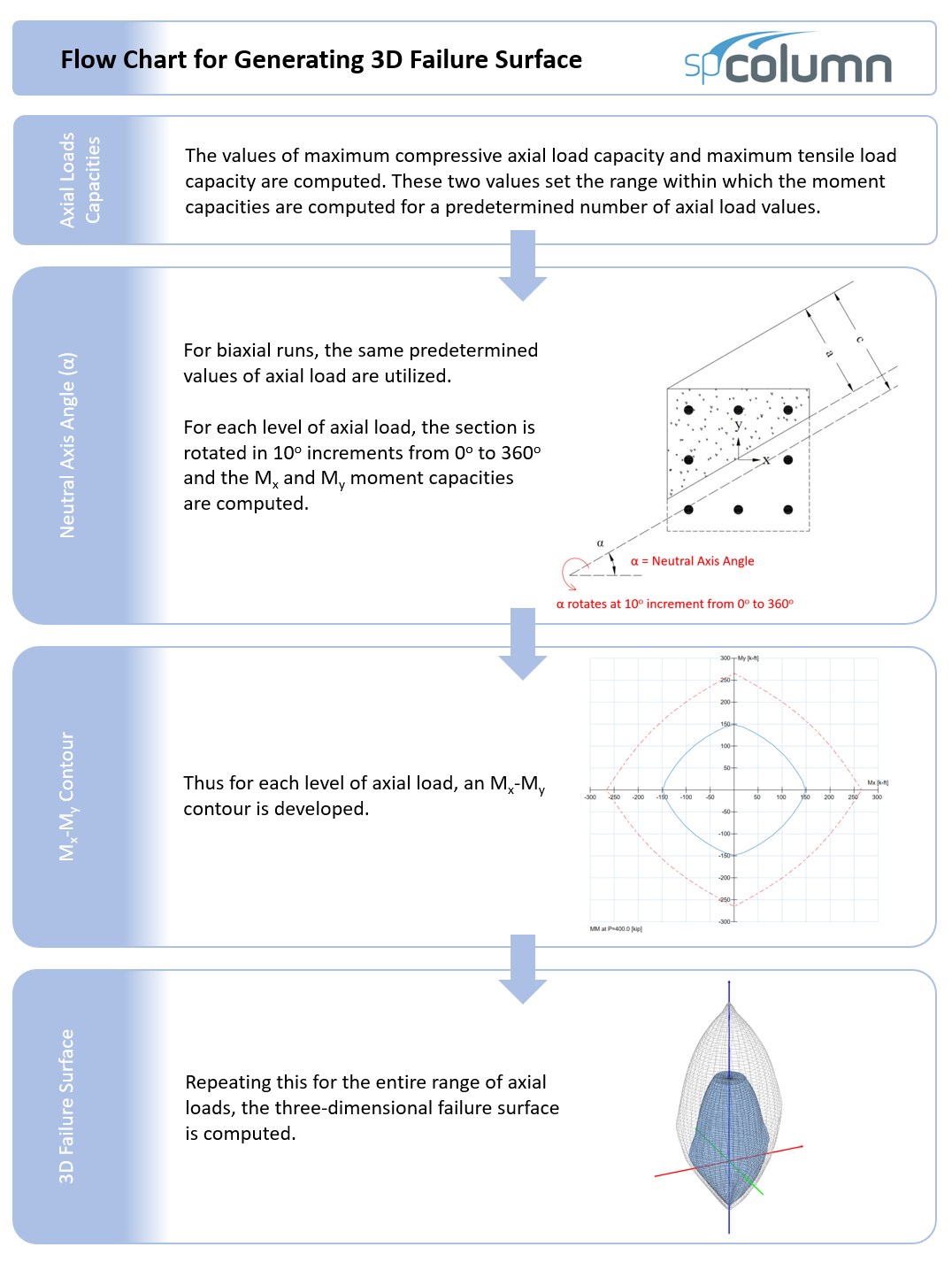
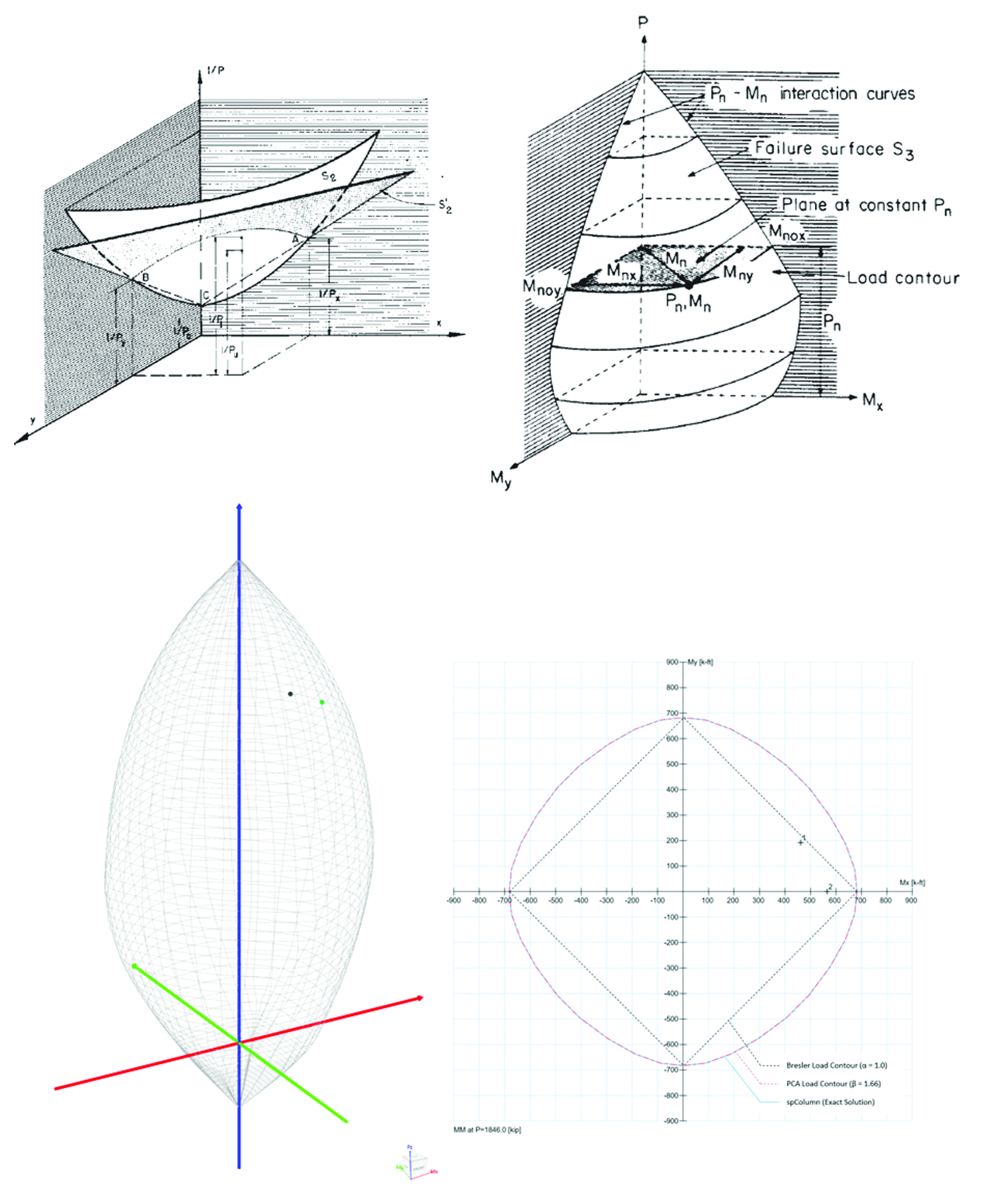
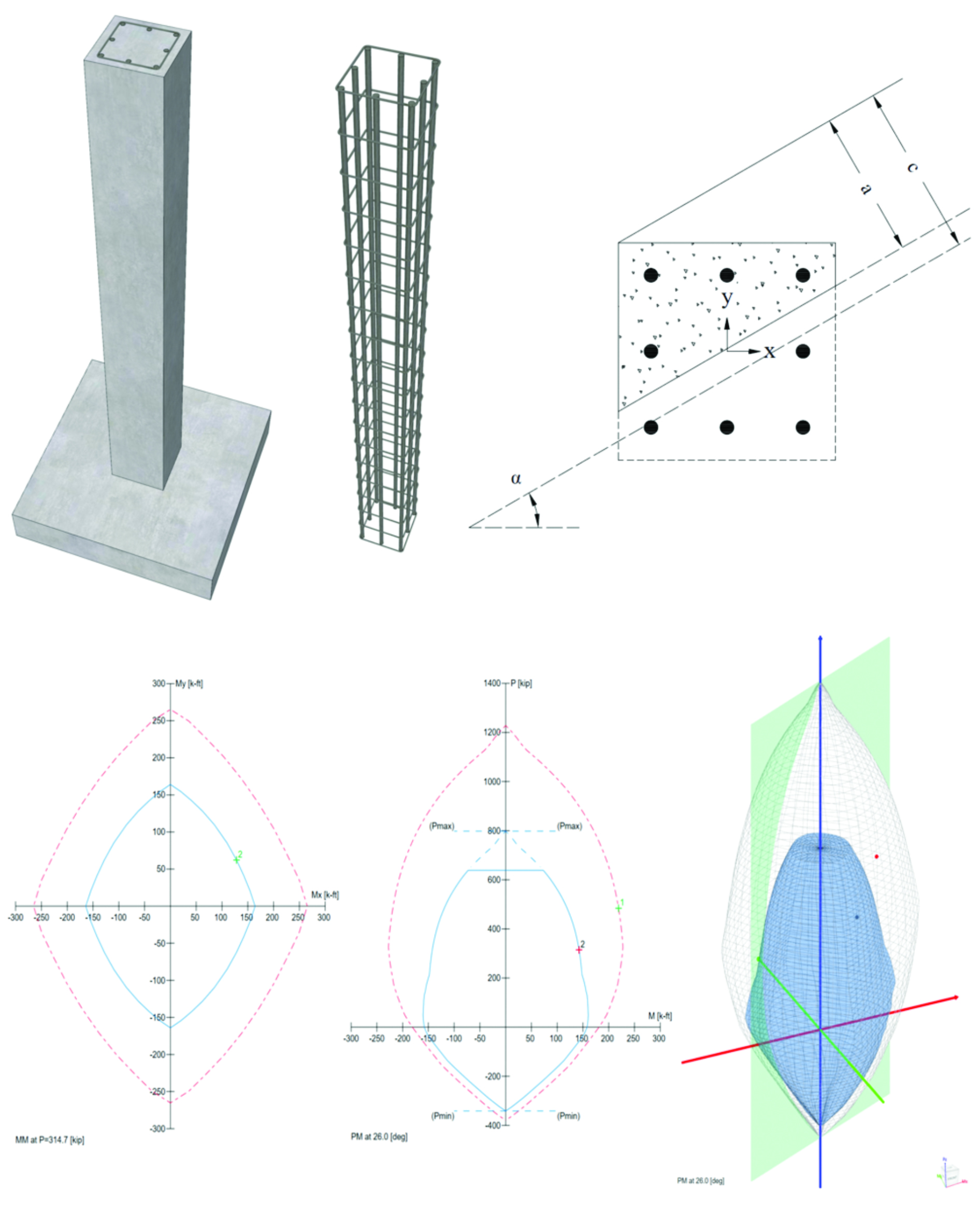
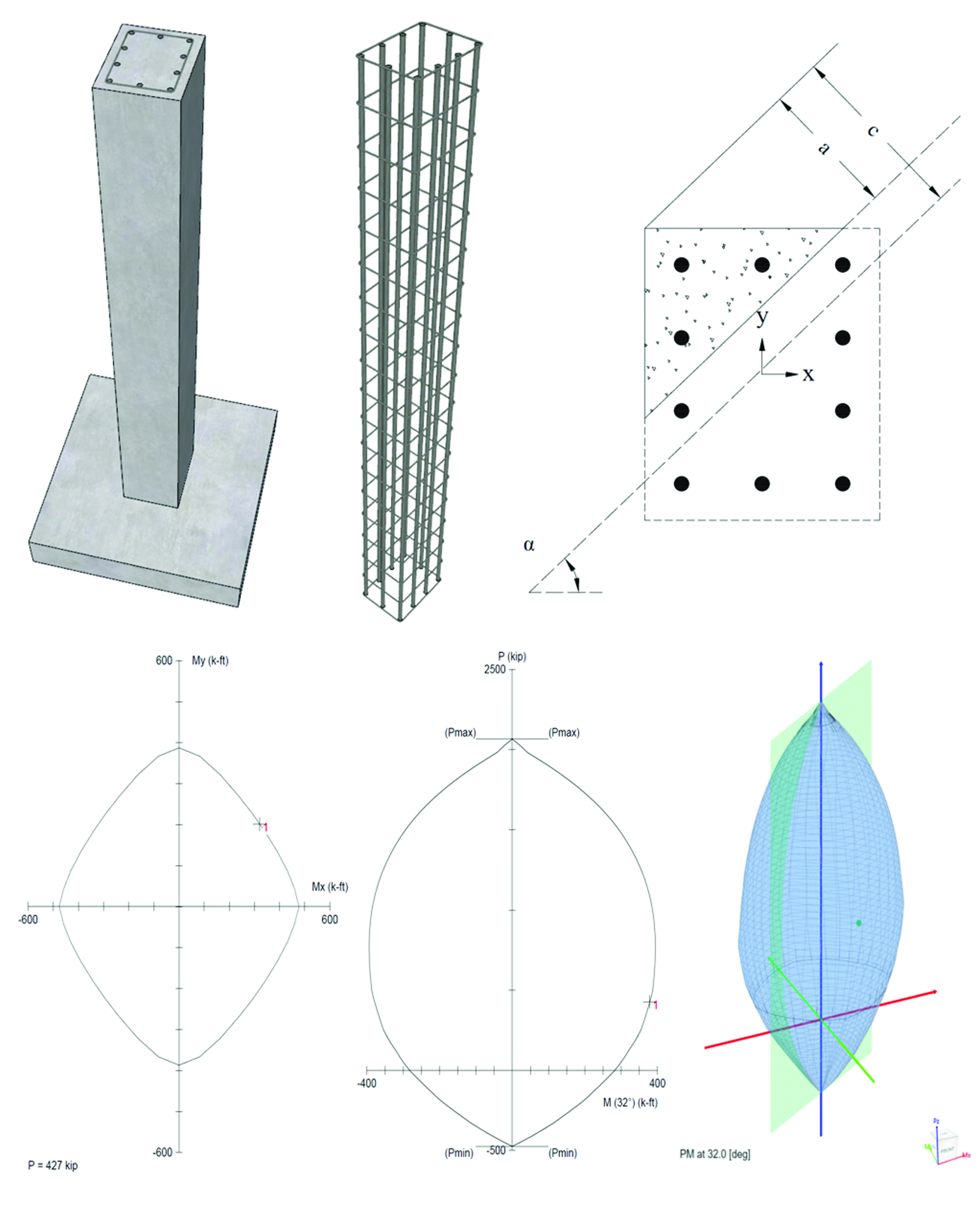
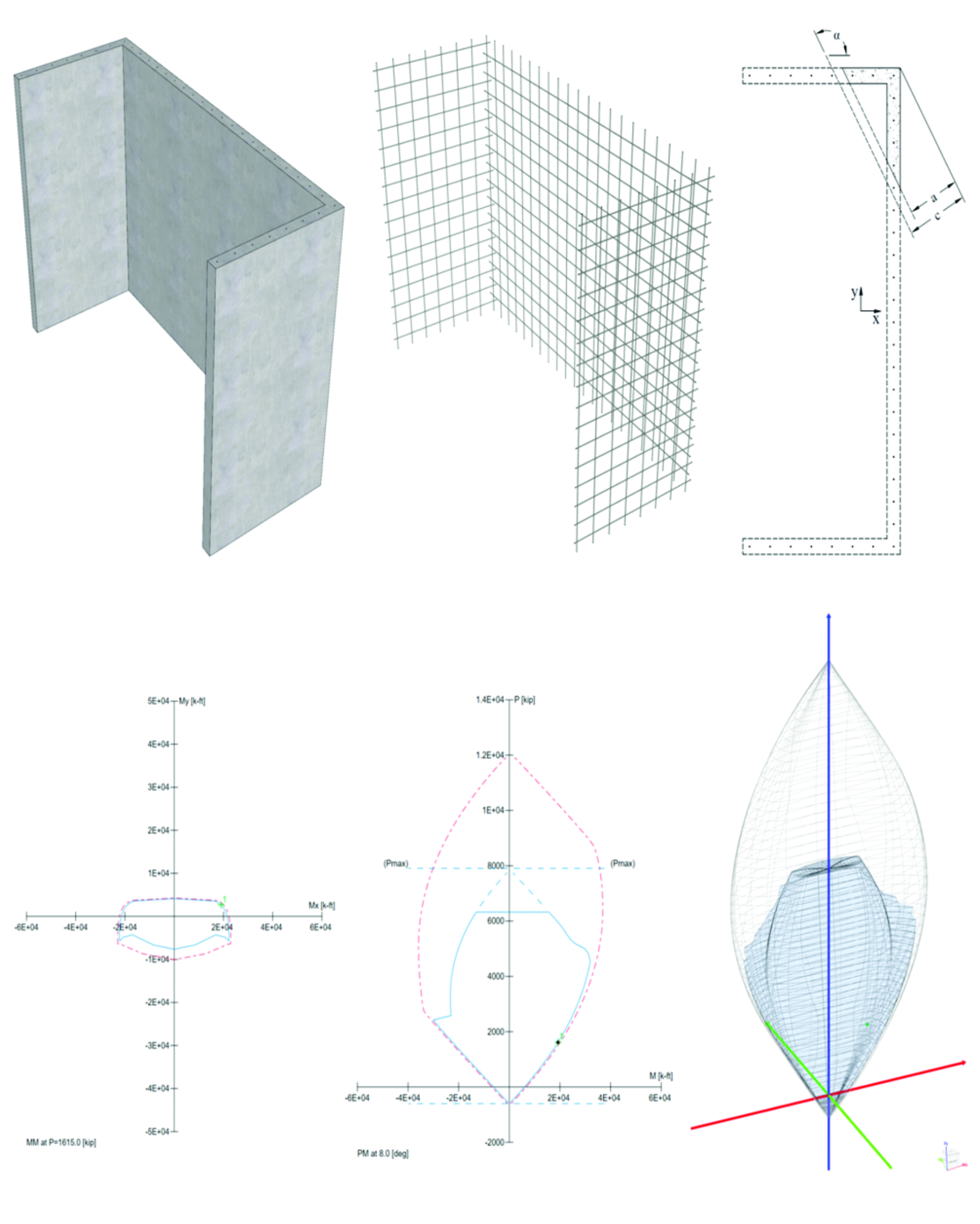
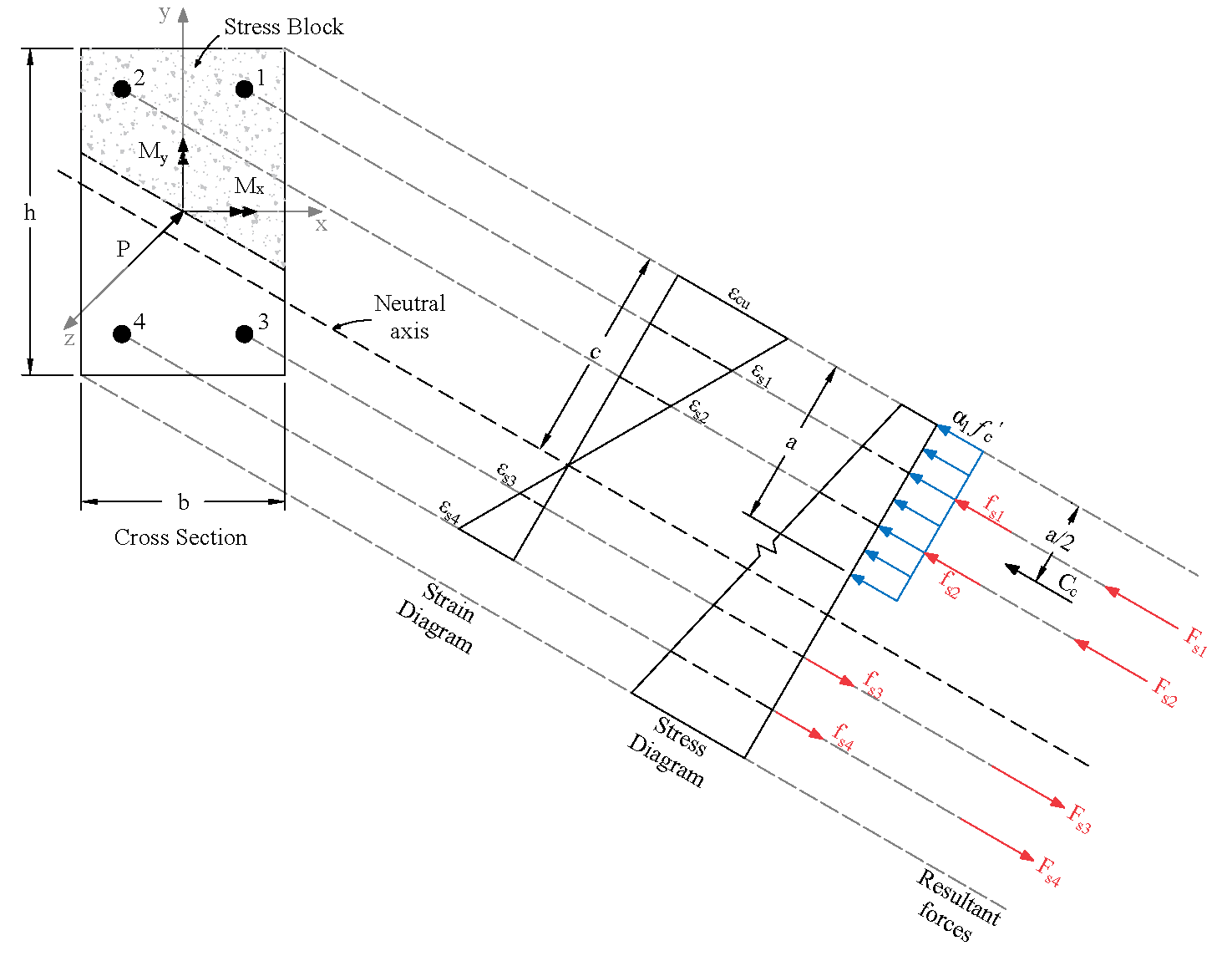
Section Analysis

The analysis of the reinforced concrete section performed by spColumn conforms to the provisions of the Strength Design Method (CSA A23.3) and Unified Design provisions (ACI 318). All conditions of strength satisfy the applicable conditions of equilibrium and strain compatibility.

Analysis of Reinforced Concrete Section

Reduction Factors

For the ACI codes, the nominal (unreduced) capacity of the section is first computed. Then, the nominal capacity is reduced to the design capacity using the strenth reduction factor, Φ.

Reduction Factors for Flexural and Axial Capacity per ACI code

Section Investigation

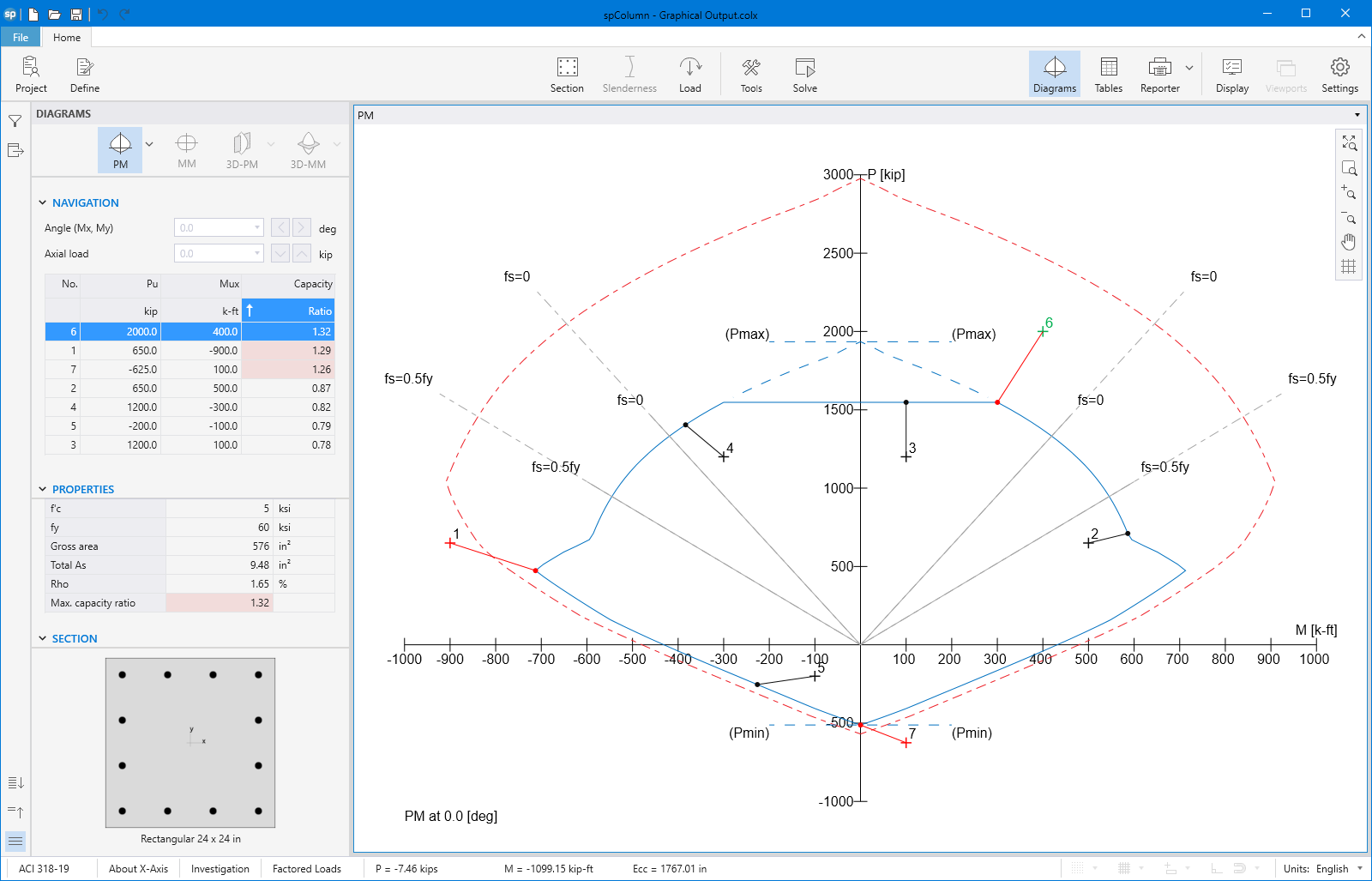
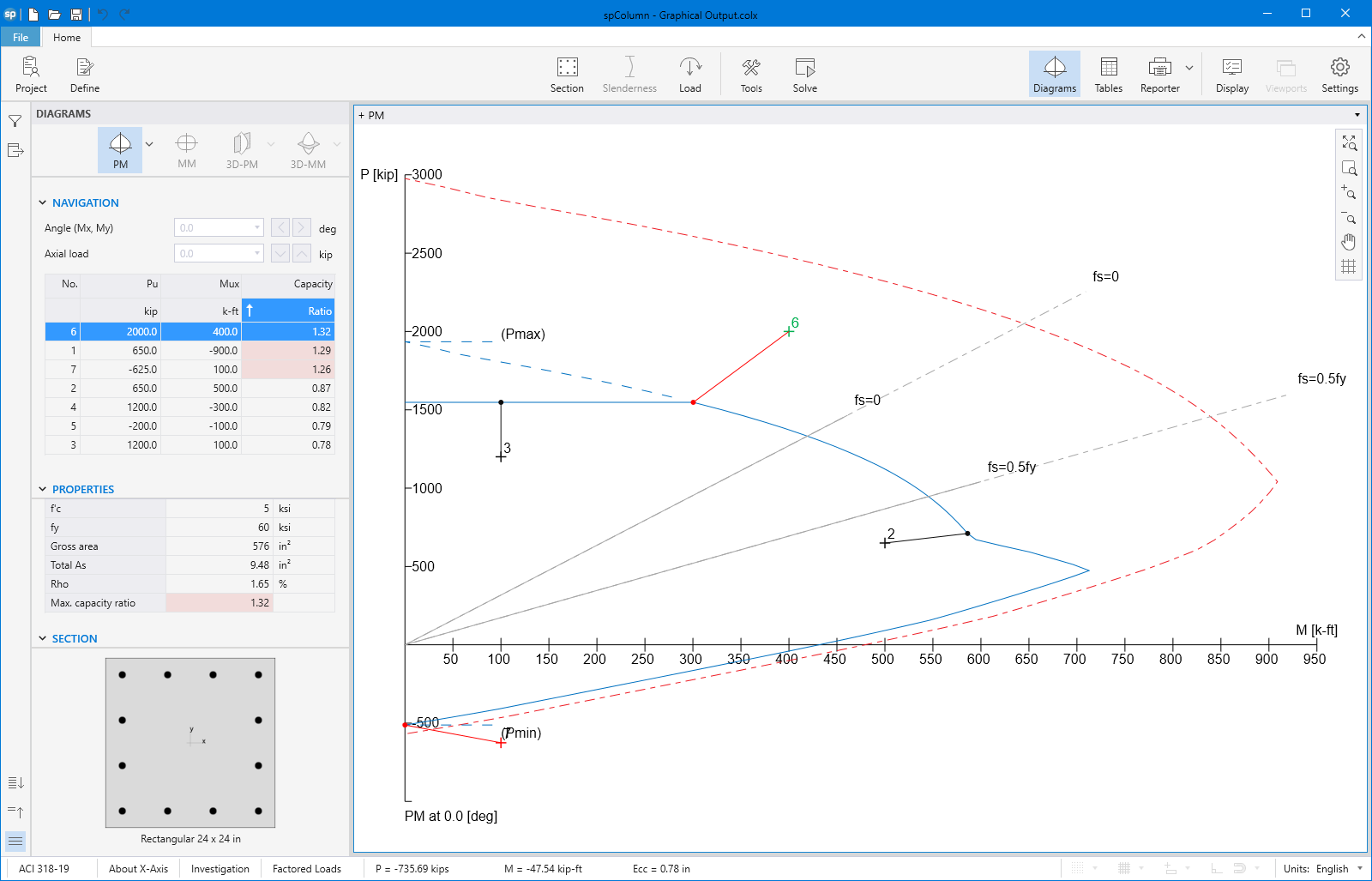
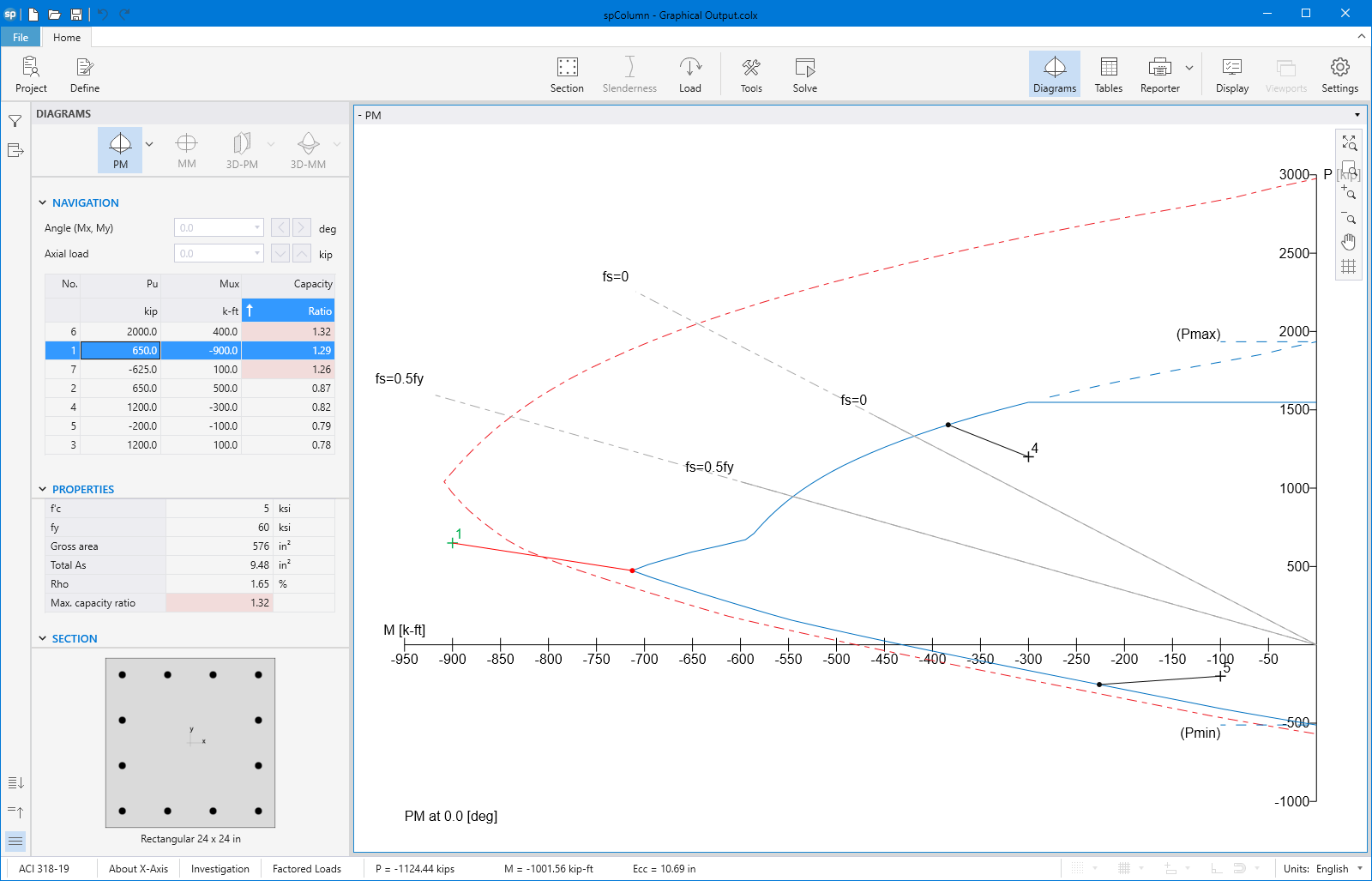
spColumn computes the interaction diagram (uniaxial runs) or the three-dimensional failure surface (biaxial runs) of the input section. The values of maximum compressive axial load capacity and maximum tensile load capacity are computed. These two values set the range within which the moment capacities are computed for a predetermined number of axial load values.

For uniaxial runs, positive and negative moment capacities about only the selected axis are computed. Moment capacities about the orthogonal axis are ignored. To compute the moment capacity at a certain level of axial load, the neutral axis angle is held constant, parallel to the selected axis. The neutral axis depth is adjusted to arrive at the desired axial load capacity. This is done for all the predetermined values of axial load.
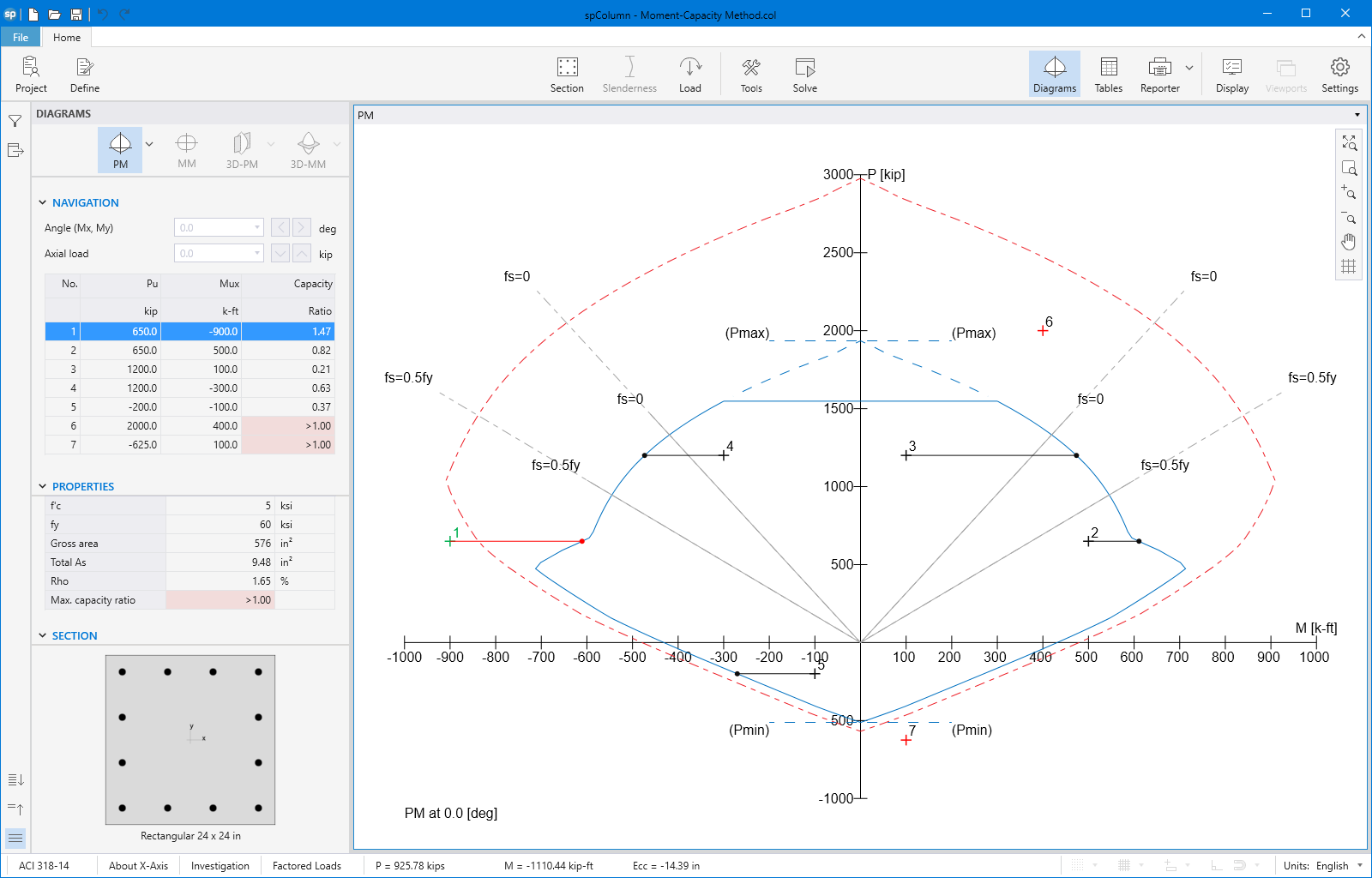
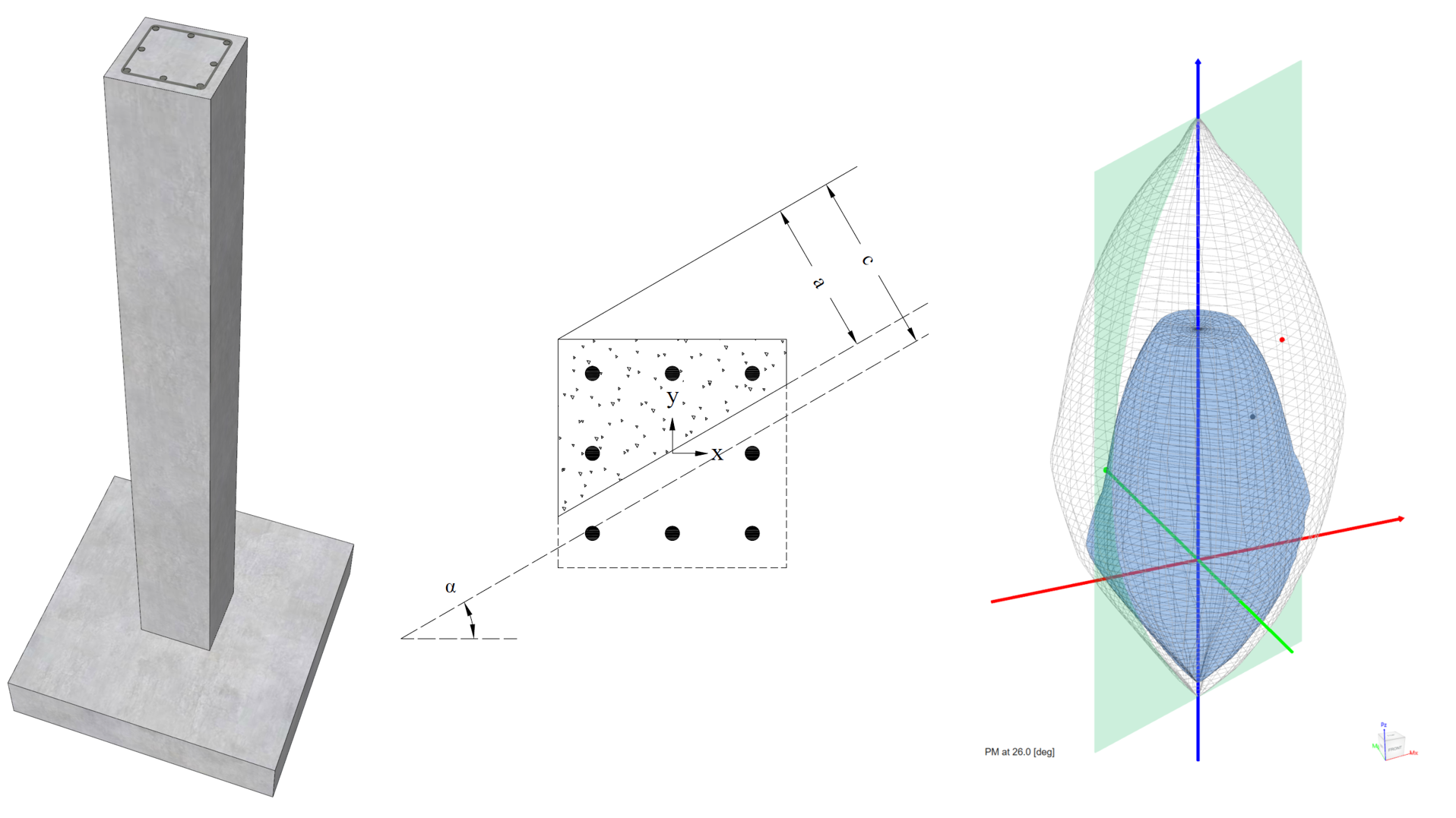
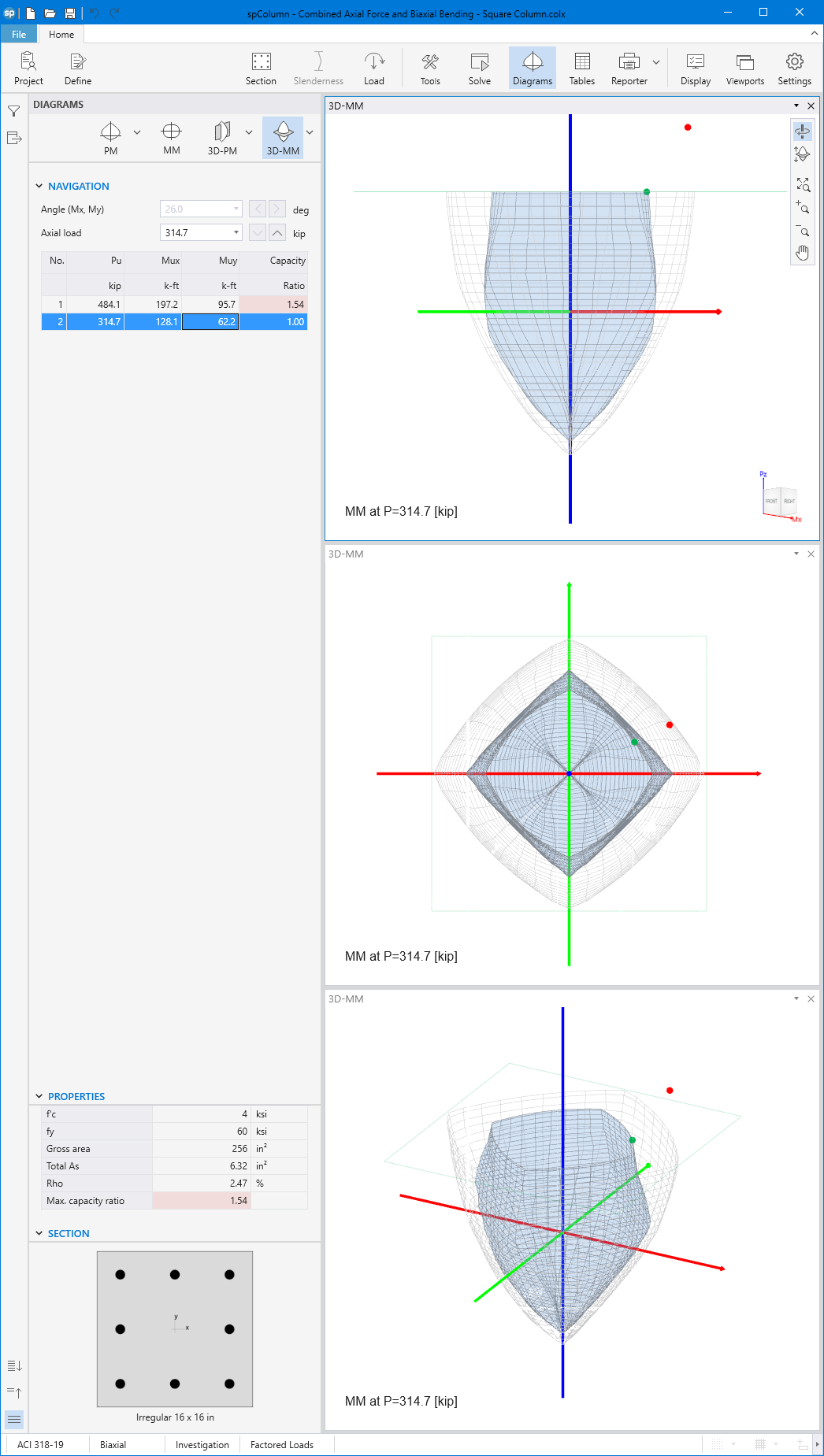
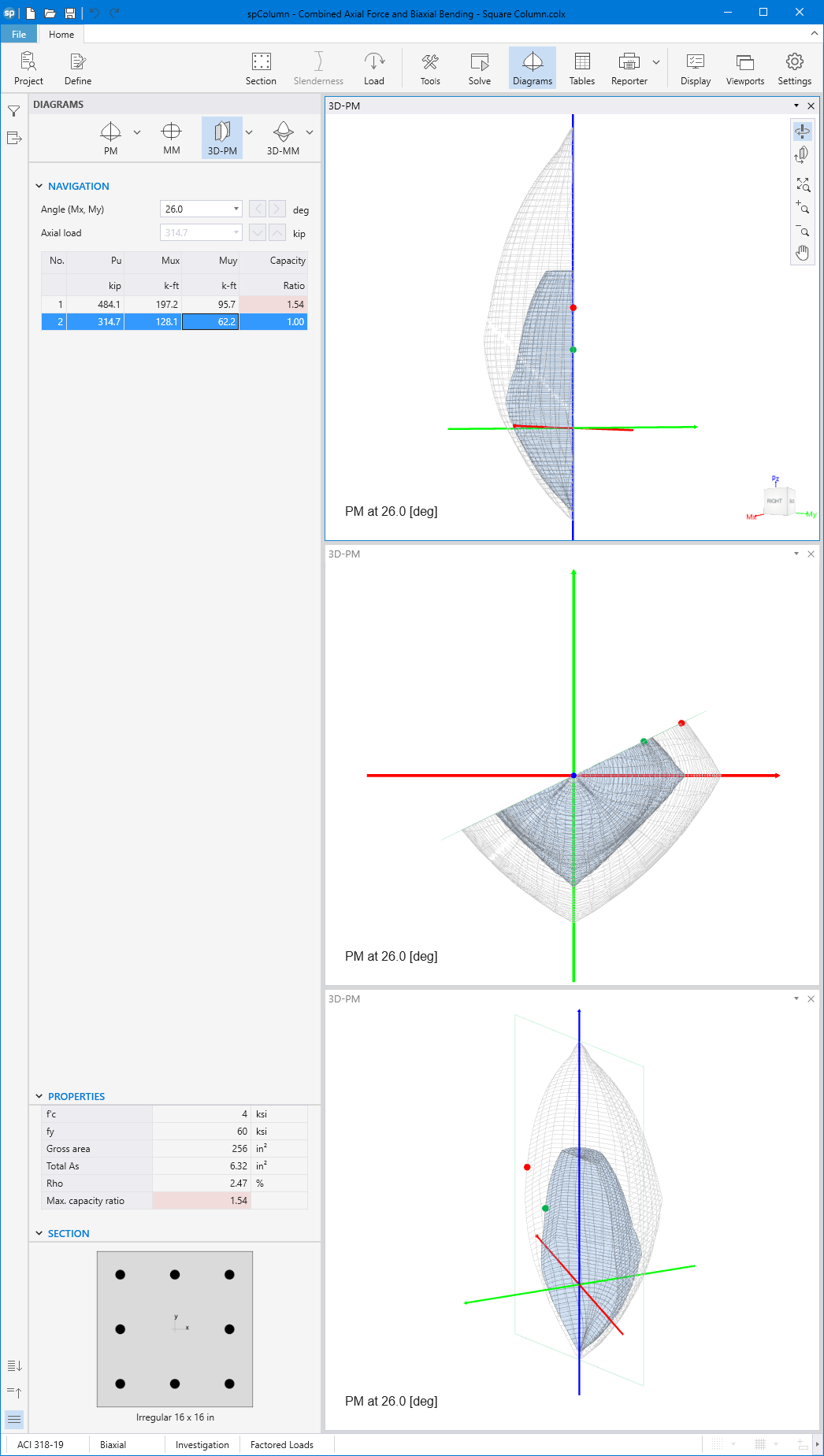
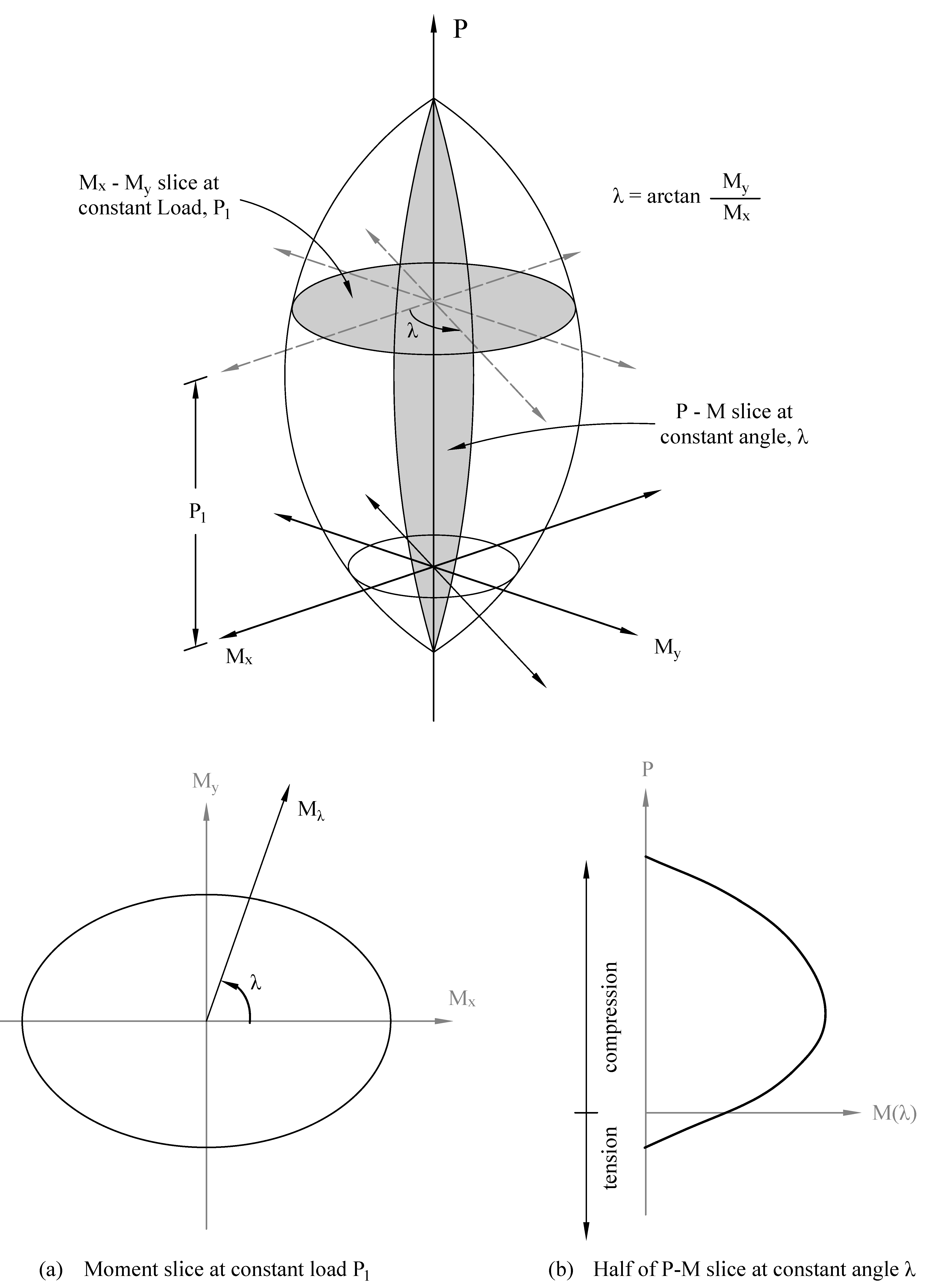
For biaxial runs, the same predetermined values of axial load are utilized. For each level of axial load, the section is rotated in 10-degree increments from 0 degrees to 360 degrees and the Mx and My moment capacities are computed. Thus for each level of axial load, an Mx-My contour is developed. Repeating this for the entire range of axial loads, the three-dimensional failure surface is computed. A three-dimensional visualization of the resulting entire nominal and factored failure surface is provided to support enhanced understanding of section capacity.

Interaction Surface for Combined Axial Load and Biaxial Bending

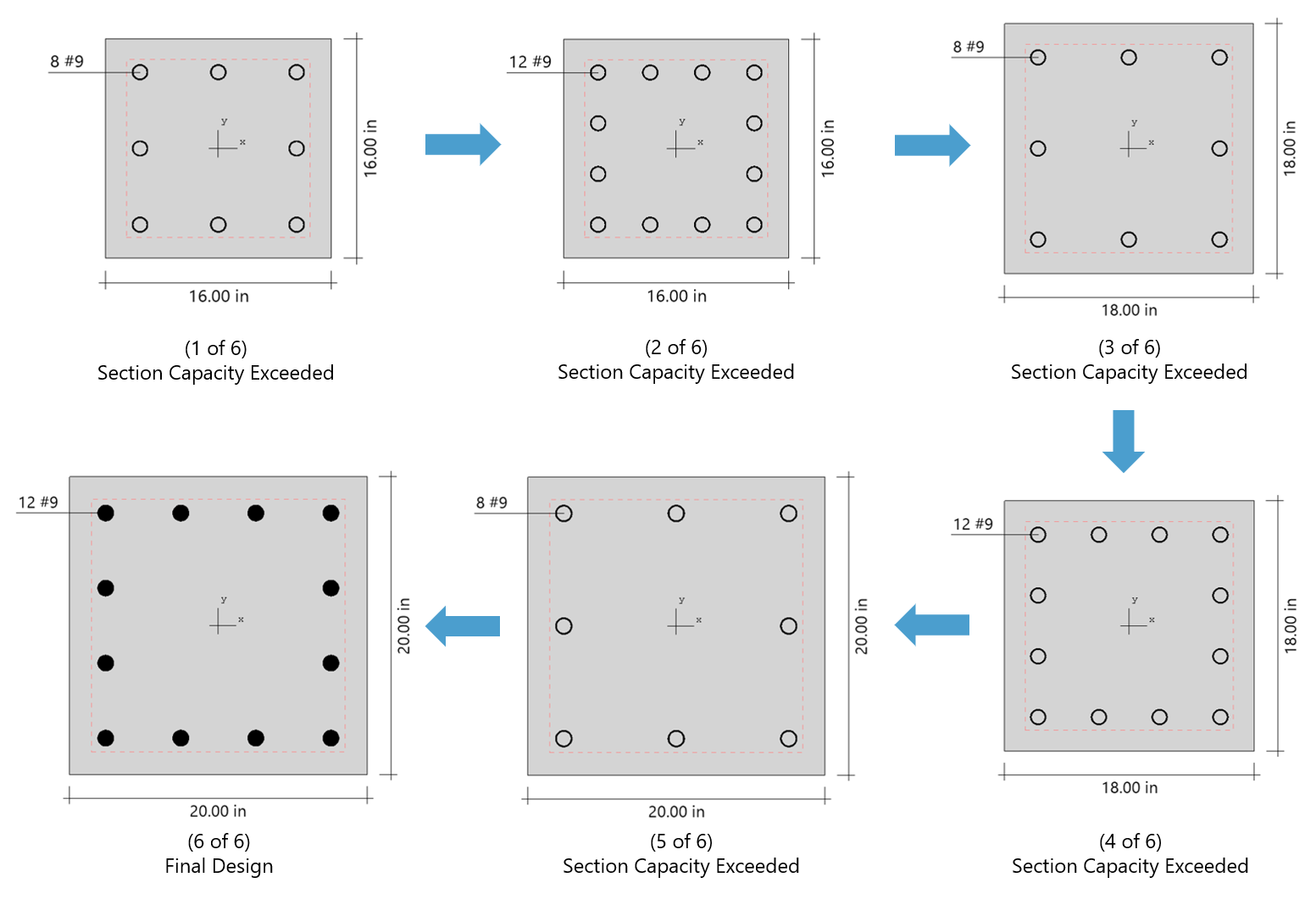
Section Design

Based on the specified minimum, maximum and increment specified for the section and the reinforcing bars, the program selects the smallest section with the least amount of reinforcement for which the load-moment capacity exceeds the appplied loads. Depending on the design criteria the user selects, the least amount of reinforcement the program searches for means either the smallest number of bars or the smallest steel area.

Section Design Process

To the top

Results Output

Graphical Output

P-M Diagram - Full

P-M Diagram - M Positive

P-M Diagram - M Negative

Mx-My Diagram [Biaxial Runs Only]

3D-PM and 3D-MM Views [Biaxial Runs Only]

Text Output Tabular Output

Slenderness Input Summary

Moment Magnification Factors

Factored Moment Due to First-Order and Second-Order Effects

Control Points

Factored Loads and Moments with Corresponding Capacities

To the top

Demand Capacity Ratio (DCR)

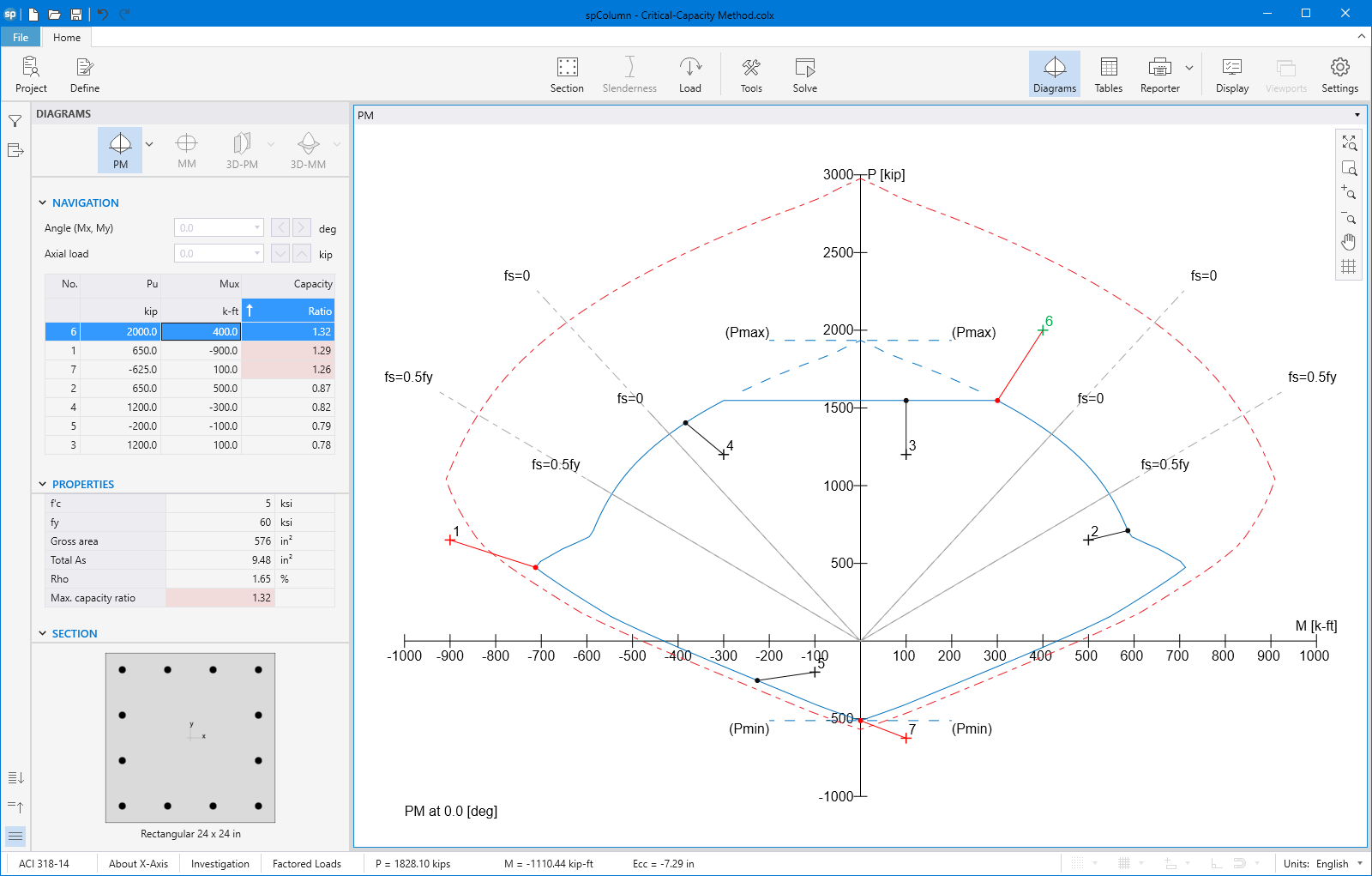
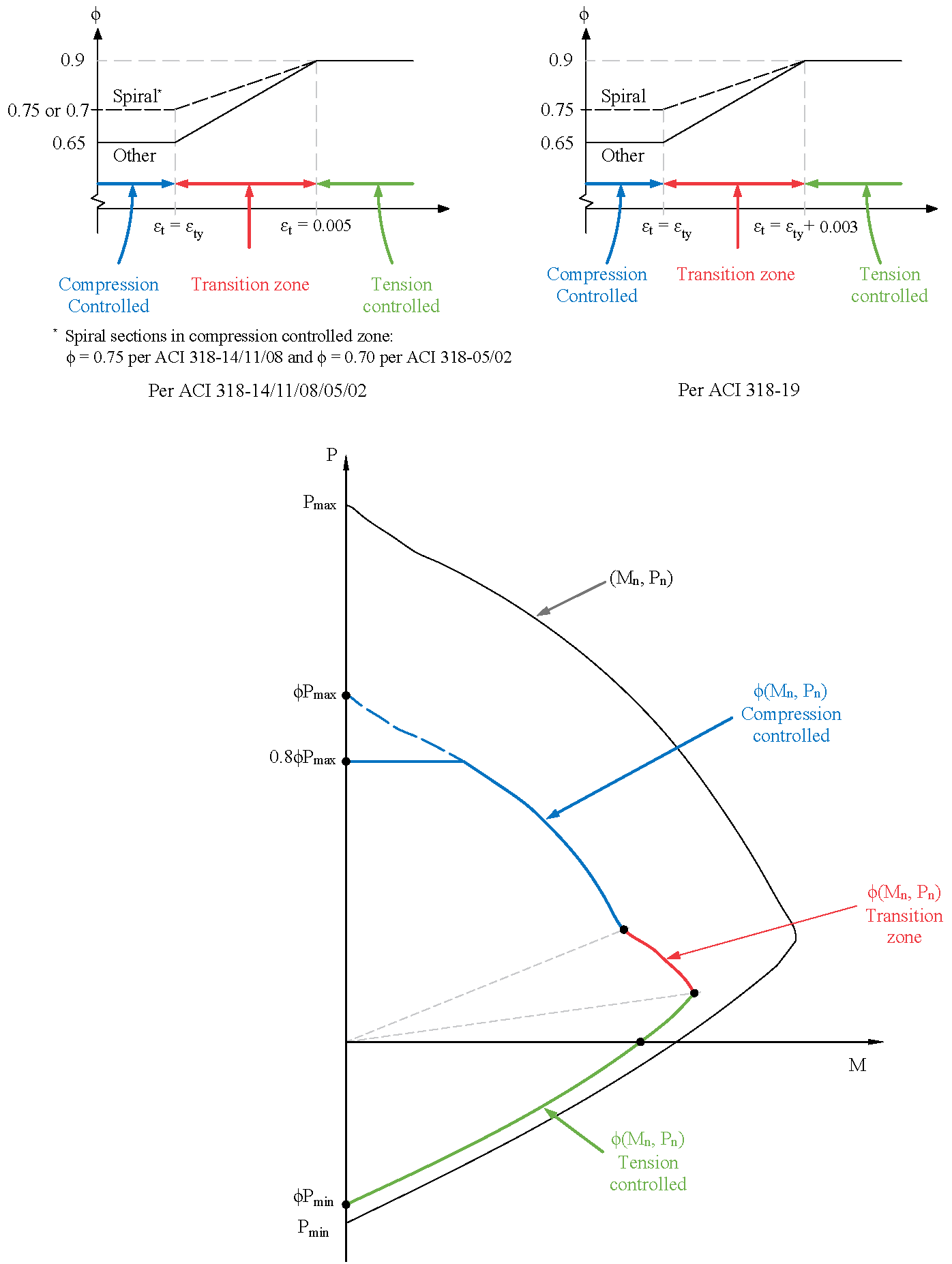
The program can compute the section demand capacity ration in one of the two available methods, namely, Moment-Capacity Method and Critical-Capacity Method.

Moment-Capacity Method

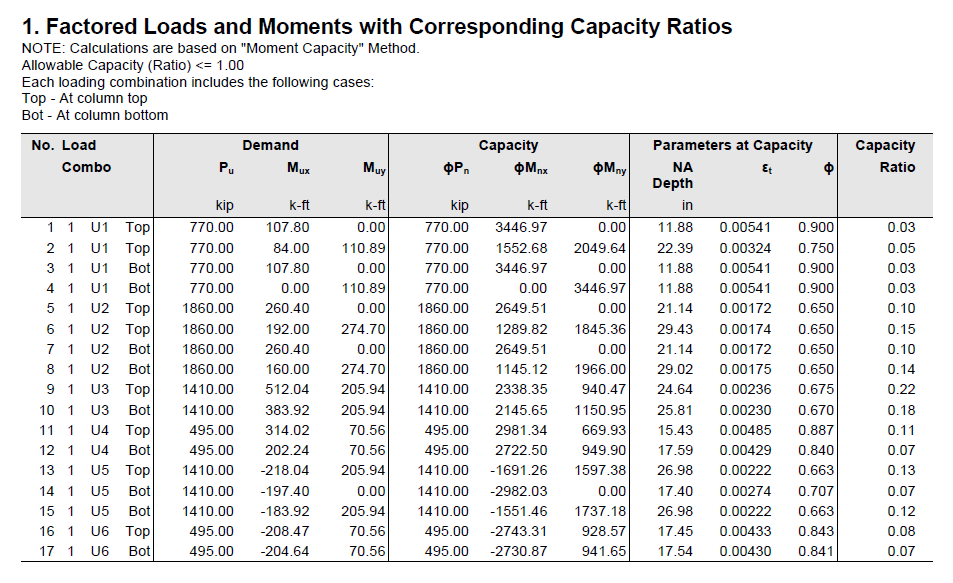
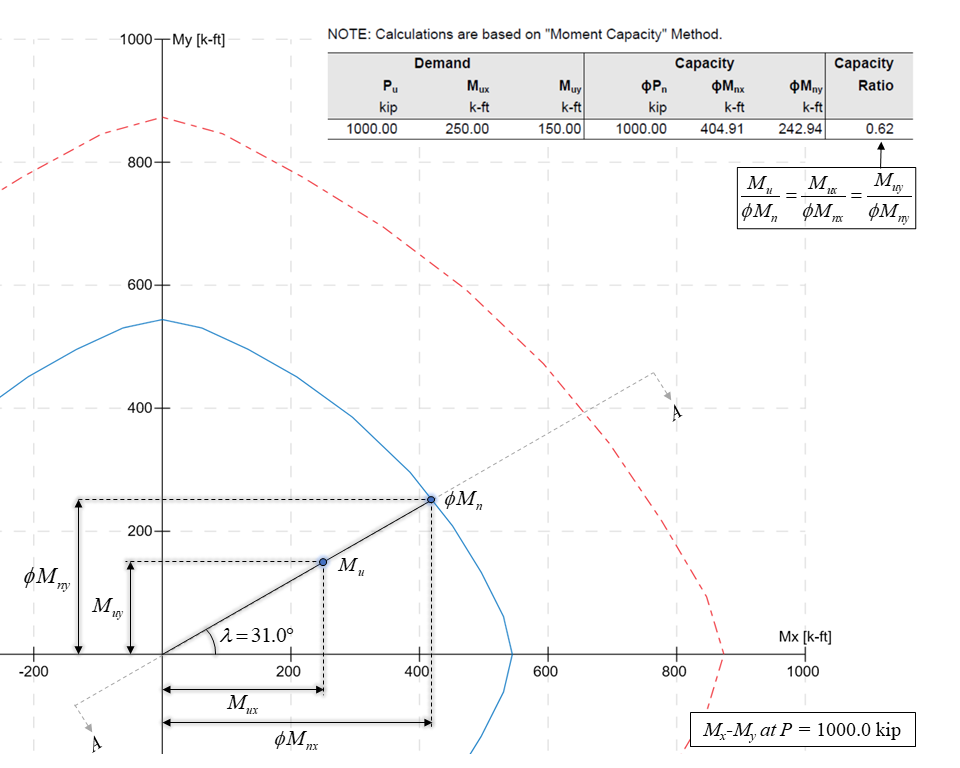
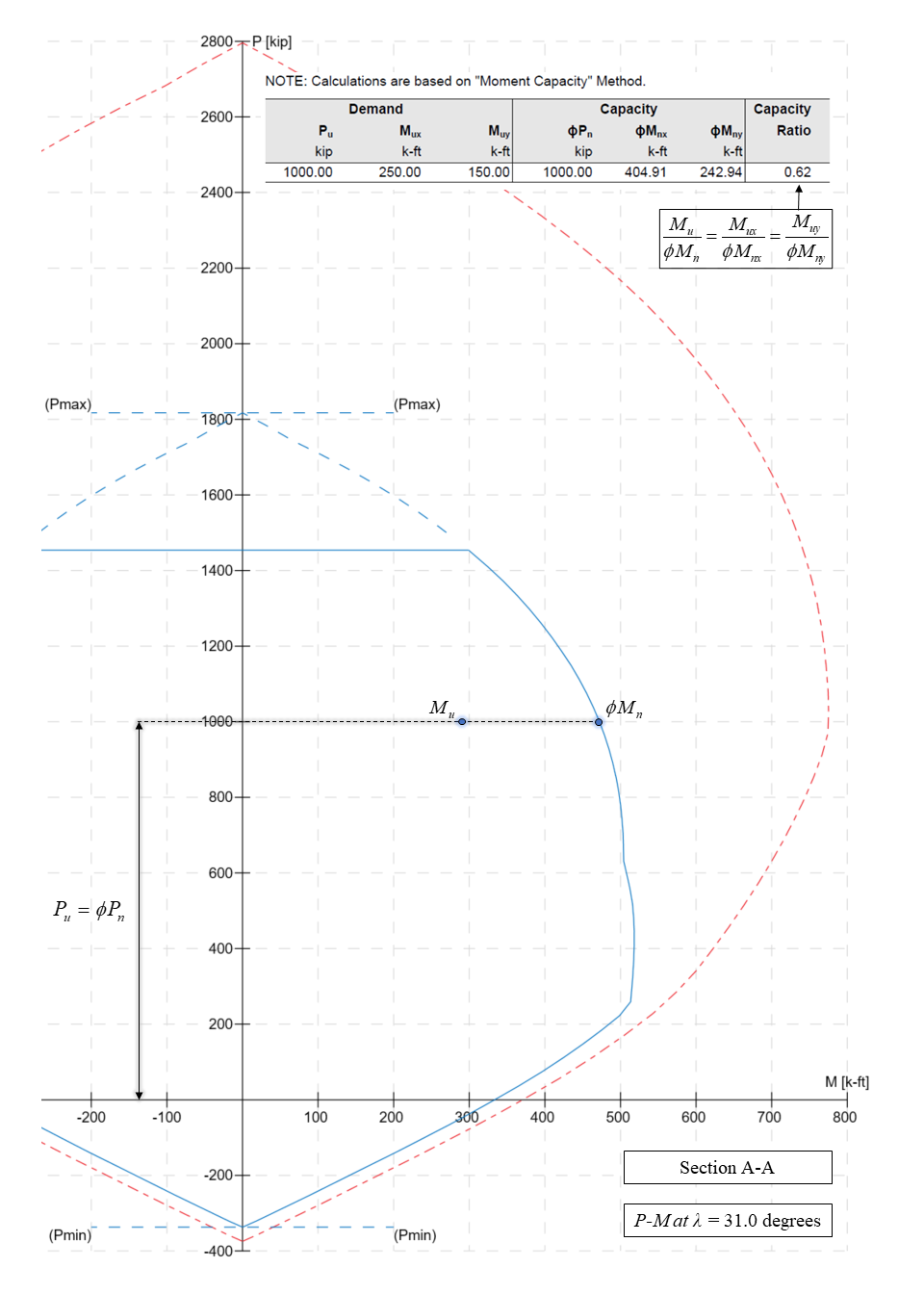
Moment-Capacity Method calculates the section capacity as the ratio of moment demand, Mu to moment capacity, ΦMn. When a unique value of ΦMn cannot be calculated for a given load point, this method gives the capacity ratio as "> 1" or "< 1" depending on the location of the point.

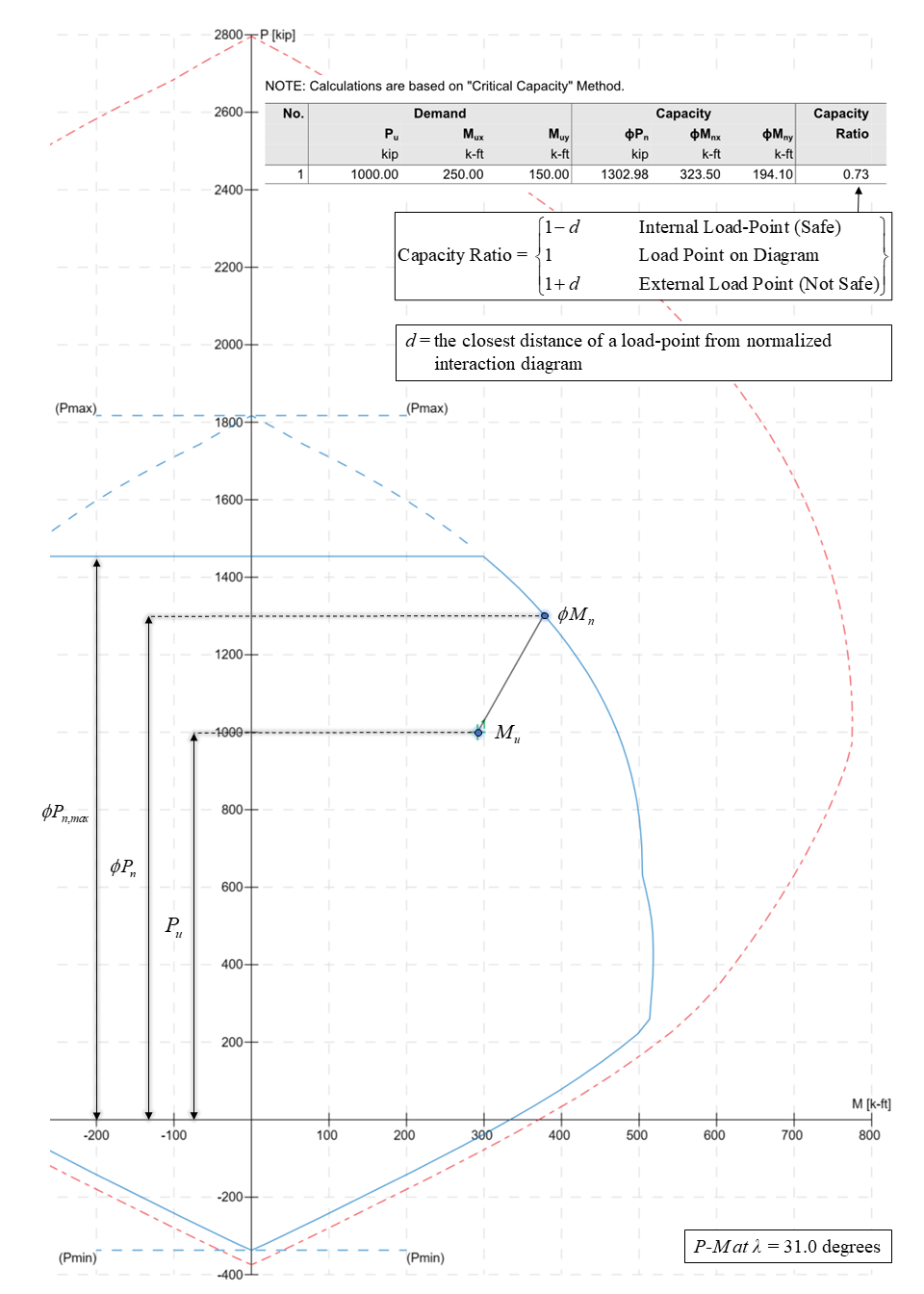
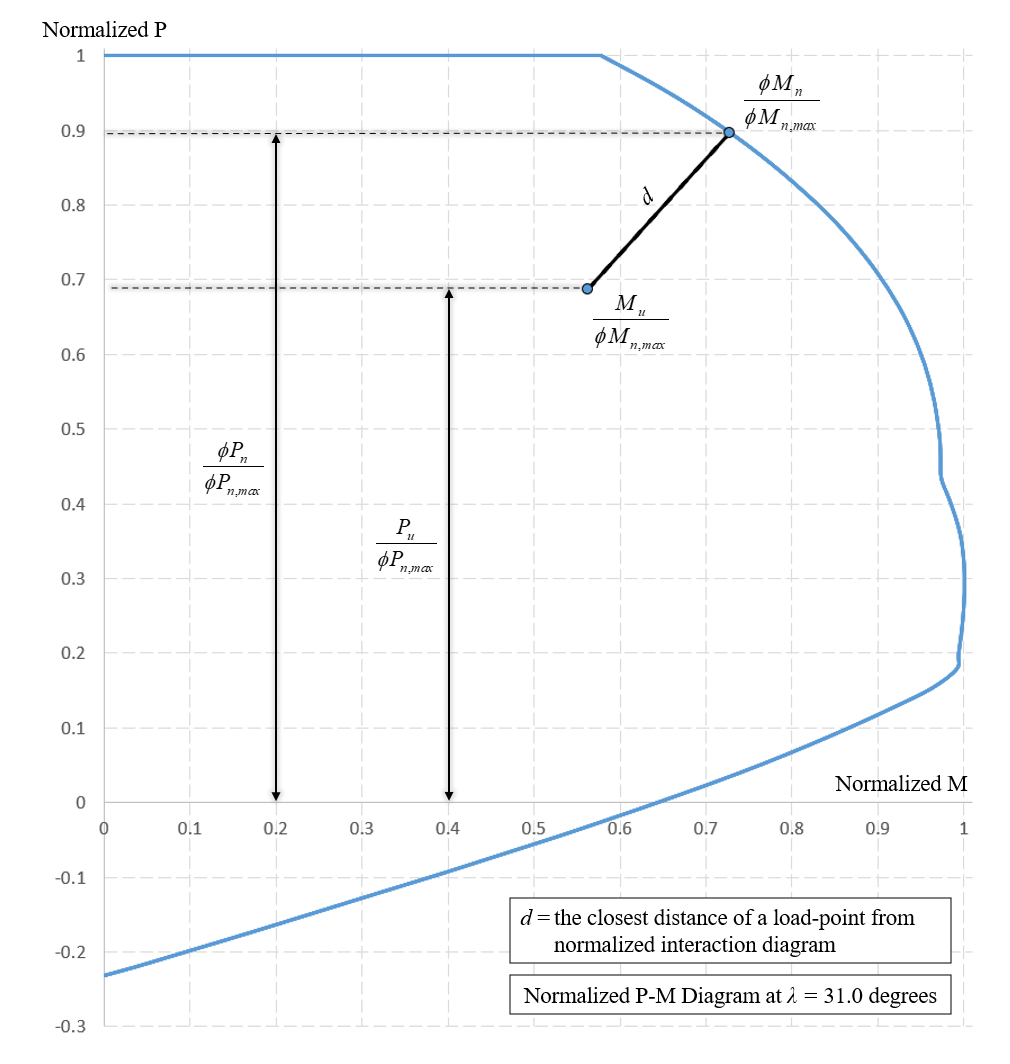
Capacity Ratio Per Moment-Capacity Method

Critical-Capacity Method

Critical-Capacity Method calculates the section capacity based on the closest distance to a load-point from the normalized interaction diagram. More information on normalized interaction diagram and calculation of the closest distance, d, can be found in spColumn Manual.

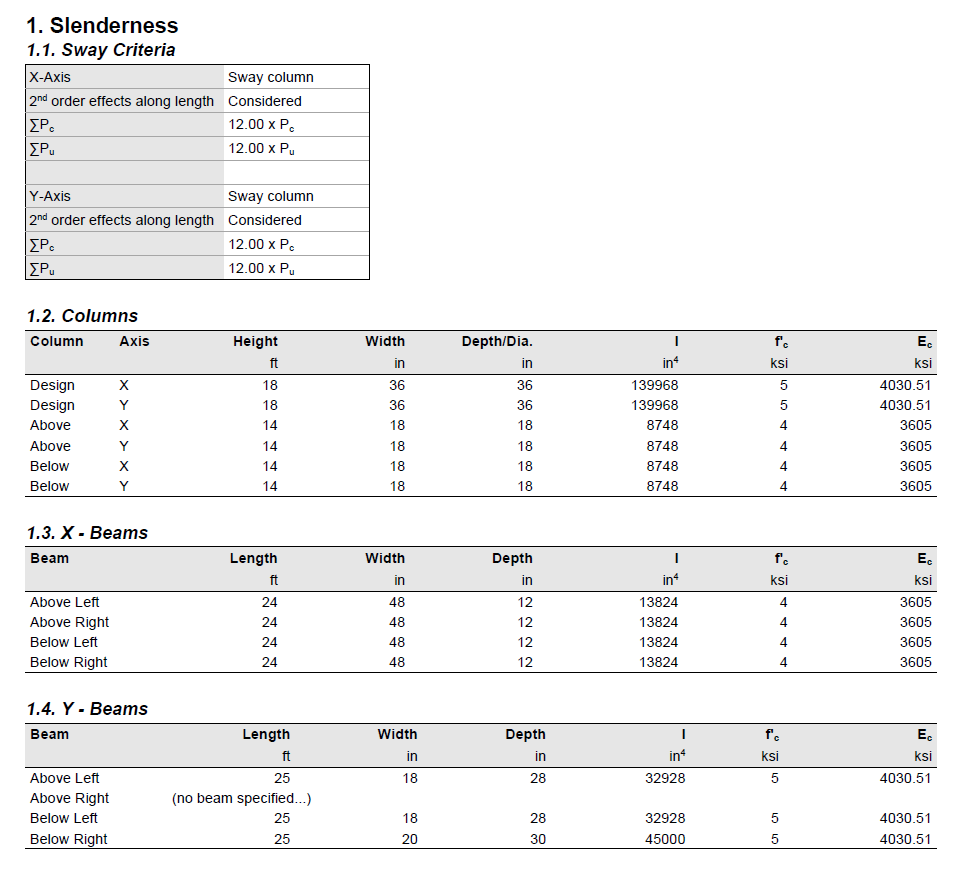
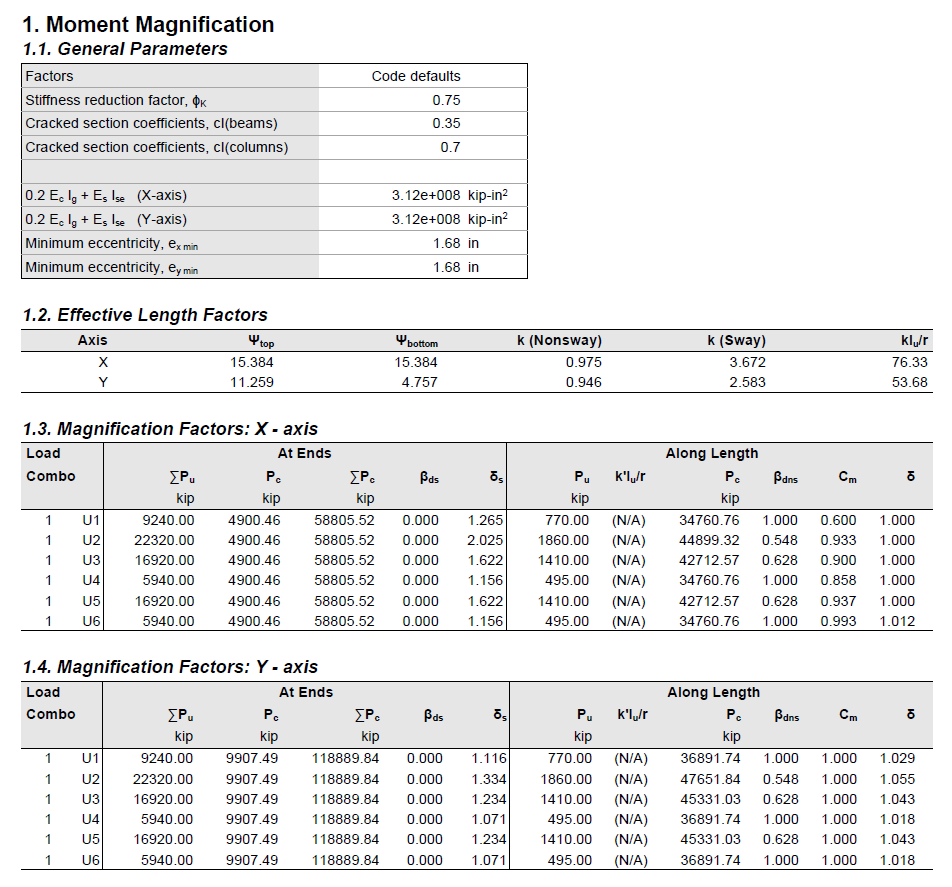
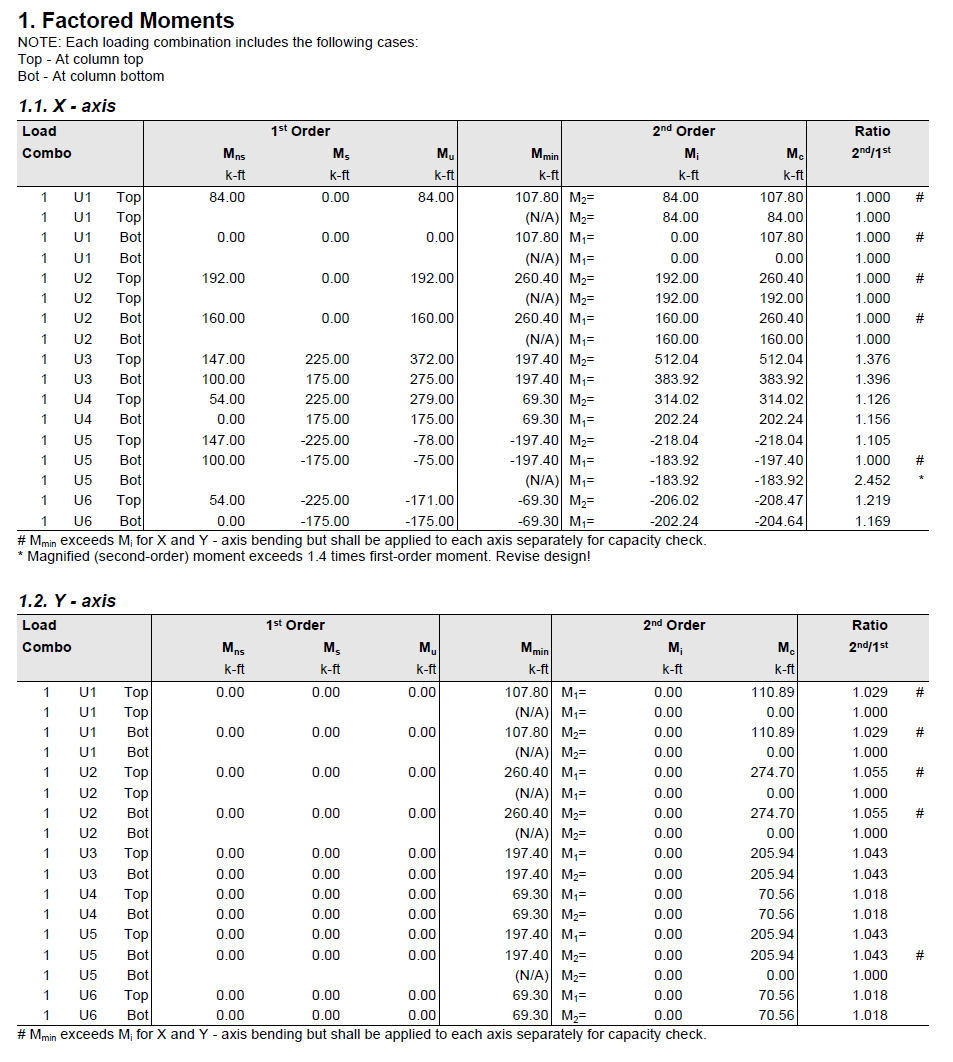
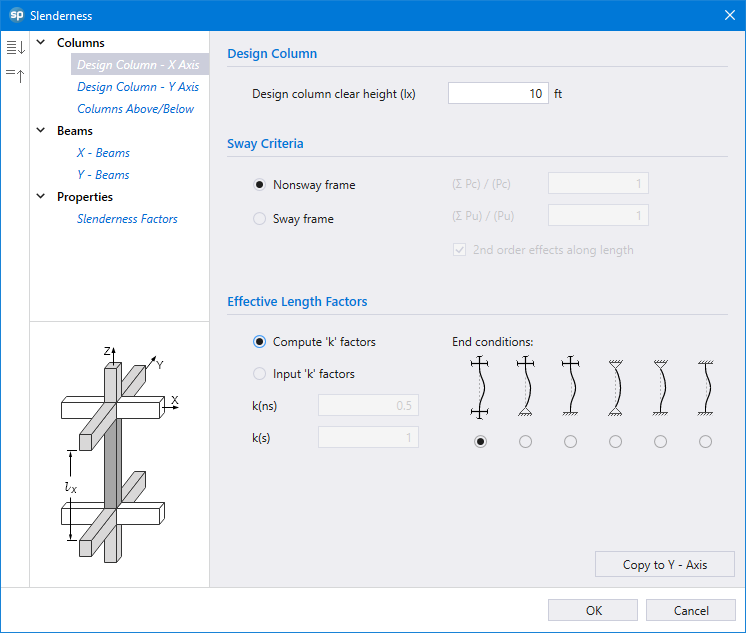
Capacity Ratio Per Critical-Capacity Method

To the top

Slenderness Effects

Column slenderness is expressed in terms of its slenderness ratio klu/r, where k is an effective length factor (dependent on rotational and lateral restrains at the ends of the column), lu is unsupported column length, and r is the radius of the gyration of the column cross-section. In general, a column is slender if its aplicable cross-sectional dimension is small in comparison to its length.

Slenderness effects producing magnified moments through moment magnification procedure (ACI 318 and CSA A23.3) can be considered both for design and investigation of sections in lieu of complicated and time consuming 3D analytical models.

Slenderness consideration:

Learn how to apply slenderness effects

Slenderness Examples:

Step-by-step written guide on how to consider slenderness

Detailed Calculation Example:

Second order effects using moment magnification method (ACI 318-14)

Technical Article:

Flexural Stiffness for Critical Buckling Load (ACI 318-14)

Slenderness Methodology:

Process flowchart for determining column slenderness effects using

ACI 318-14
ACI 318-19

Slenderness Equations:

Equations flowchart for determining column slenderness effects using

ACI 318-14
ACI 318-19

Video Tutorial:

Step-by-step video guide on how to consider slenderness

Observations:

Commentary on moment magnification irregularities

All-Inclusive Presentation:

In-depth presentation on slenderness considerations in column analysis & design

Flowchart for Determining Column Slenderness Effects

Process Flowchart

Equation Flowchart

To the top

Combined Axial Load and Biaxial Bending

3D Failure Surface for Combined Axial Load and Biaxial Bending

In most building design calculations, all building columns may be subjected to biaxial bending (Mx and My) due to lateral effects and unbalanced moments from both directions of analysis. This requires an investigation of the column P-Mx-My interaction diagram in two directions simultaneously (axial force interaction with biaxial bending).

Generating the three-dimensional failure surface (interaction diagram) for a column section subjected to a combined axial force and biaxial bending moments is tedious and challenging for engineers. The use of a computer aid can save time and eliminate errors.

StructurePoint's spColumn program can quickly, simply and accurately generate the three-dimensional failure surface (interaction diagram) for all commonly encountered column, beam or wall sections in addition to highly complex and irregular cross-sections.